13.9: Juego tímido
- Page ID
- 152089
Teoría Básica
Recordemos que con la estrategia del juego tímido en rojo y negro, la jugadora hace una pequeña apuesta constante, digamos $1, en cada juego hasta que se detiene. Así, en cada juego, la fortuna del jugador o bien aumenta en 1 o disminuye en 1, hasta que la fortuna alcanza o bien 0 o el objetivo\(a\) (que suponemos que es un entero positivo). Así, el proceso de la fortuna\((X_0, X_1, \ldots)\) es una caminata aleatoria sobre el espacio de la fortuna\(\{0, 1, \ldots, a\}\) con 0 y\(a\) como barreras absorbentes.
Como es habitual, nos interesa la probabilidad de ganar y el número esperado de juegos. La idea clave en el análisis es que después de cada juego, el proceso de la fortuna simplemente comienza de nuevo, pero con un valor inicial diferente. Este es un ejemplo de la propiedad de Markov, que lleva el nombre de Andrei Markov. Un capítulo separado sobre Cadenas de Markov explora estos procesos aleatorios con más detalle. En particular, este capítulo tiene secciones sobre Cadenas de Nacimiento-Muerte y Caminatas Aleatorias sobre Gráficas, clases particulares de cadenas de Markov que generalizan los procesos aleatorios que aquí estamos estudiando.

La probabilidad de ganar
Nuestro análisis basado en la propiedad de Markov sugiere que tratamos la fortuna inicial como una variable. Así, denotaremos la probabilidad de que el jugador alcance el objetivo\(a\), comenzando con una fortuna inicial\(x\) por\[ f(x) = \P(X_N = a \mid X_0 = x), \quad x \in \{0, 1, \ldots, a\} \]
La función\(f\) satisface las siguientes condiciones de ecuación de diferencia y límite:
- \(f(x) = q f(x - 1) + p f(x + 1)\)para\( x \in \{1, 2, \ldots, a - 1\}\)
- \(f(0) = 0\),\(f(a) = 1\)
Prueba
Las condiciones de contorno son solo una cuestión de definición. La ecuación de diferencia se deriva del condicionamiento sobre el resultado del primer ensayo. Ella pierde este juicio con probabilidad\(q\) y si pierde, entonces efectivamente inicia una nueva secuencia de juicios pero con fortuna inicial\(x - 1\). Ella gana el primer juicio con probabilidad\(p\), y si gana, entonces efectivamente inicia una nueva secuencia de pruebas pero con fortuna inicial\(x + 1\).
La ecuación de diferencia es lineal (en la función desconocida\(f\)), homogénea (porque cada término involucra a la función desconocida\(f\)) y de segundo orden (porque 2 es la diferencia entre las fortunas más grandes y más pequeñas en la ecuación). Recordemos que las ecuaciones lineales homogéneas de diferencia pueden resolverse encontrando las raíces de la ecuación característica.
La ecuación característica de la ecuación de diferencia es\(p r^2 - r + q = 0\), y que las raíces son\(r = 1\) y\(r = q / p\).
Si\(p \ne \frac{1}{2}\), entonces las raíces son distintas. En este caso, la probabilidad de que el jugador llegue a su objetivo es\[ f(x) = \frac{(q / p)^x - 1}{(q / p)^a - 1}, \quad x \in \{0, 1, \ldots, a\} \]
Si\(p = \frac{1}{2}\), la ecuación característica tiene una sola raíz 1 que tiene multiplicidad 2. En este caso, la probabilidad de que el jugador llegue a su objetivo es simplemente la relación entre la fortuna inicial y la fortuna objetivo:\[ f(x) = \frac{x}{a}, \quad x \in \{0, 1, \ldots, a\} \]
Así, tenemos la distribución de la fortuna final\(X_N\) en cualquiera de los dos casse:\[ \P(X_N = 0 \mid X_0 = x) = 1 - f(x), \; \P(X_N = a \mid X_0 = x) = f(x); \quad x \in \{0, 1, \ldots, a\} \]
En el experimento rojo y negro, elige Timid Play. Varíe la fortuna inicial, la fortuna objetivo y la probabilidad de ganar el juego y observe cómo cambia la probabilidad de ganar el juego. Para diversos valores de los parámetros, ejecute el experimento 1000 veces y compare la frecuencia relativa de ganar una partida con la probabilidad de ganar una partida.
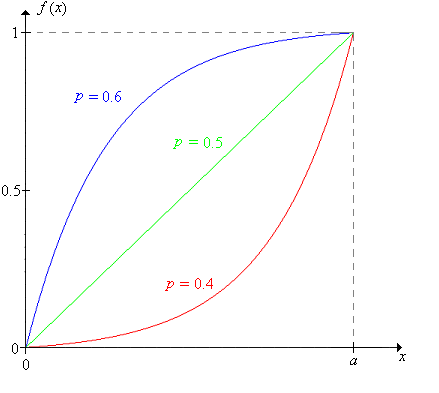
En función de\(x\), para fijos\(p\) y\(a\),
- \(f\)está aumentando de 0 a\(a\).
- \(f\)es cóncava hacia arriba si\(p \lt \frac{1}{2}\) y cóncava hacia abajo si\(p \gt \frac{1}{2}\). Por supuesto,\(f\) es lineal si\(p = \frac{1}{2}\).
\(f\)es continuo en función de\(p\), para fijos\(x\) y\(a\).
Prueba
Una aplicación de la Regla de L'Hospital muestra que la probabilidad de ganar cuando\( p \ne \frac{1}{2} \) converge a la probabilidad de ganar cuando\( p = \frac{1}{2} \), como\(p \to \frac{1}{2}\).
Para fijos\(x\) y\(a\),\(f(x)\) aumenta de 0 a 1 a medida que\(p\) aumenta de 0 a 1.
El número esperado de juicios
Ahora consideremos el número esperado de juegos necesarios con el juego tímido, cuando la fortuna inicial es\(x\):\[ g(x) = \E(N \mid X_0 = x), \quad x \in \{0, 1, \ldots, a\} \]
La función\(g\) satisface las siguientes condiciones de ecuación de diferencia y límite:
- \(g(x) = q g(x - 1) + p g(x + 1) + 1\)para\( x \in \{1, 2, \ldots, a - 1\}\)
- \(g(0) = 0\),\(g(a) = 0\)
Prueba
Nuevamente, la ecuación de diferencia se deriva del condicionamiento en el primer ensayo. Ella pierde este juicio con probabilidad\(q\) y si pierde, entonces efectivamente inicia una nueva secuencia de juicios pero con fortuna inicial\(x - 1\). Ella gana el primer juicio con probabilidad\(p\), y si gana, entonces efectivamente inicia una nueva secuencia de pruebas pero con fortuna inicial\(x + 1\). En cualquiera de los dos casos, se terminó un juicio.
La ecuación de diferencia en el último ejercicio es lineal, de segundo orden, pero no homogénea (debido al término constante 1 en el lado derecho). La ecuación homogénea correspondiente es la ecuación satisfecha por la función de probabilidad de ganancia\(f\). Así, solo se necesita un poco de trabajo adicional para resolver la ecuación no homogénea.
Si\(p \ne \frac{1}{2}\), entonces,\[ g(x) = \frac{x}{q - p} - \frac{a}{q - p} f(x), \quad x \in \{0, 1, \ldots, a\} \] ¿dónde\(f\) está la función de probabilidad de ganar arriba?
Si\(p = \frac{1}{2}\), entonces\[ g(x) = x (a - x), \quad x \in \{0, 1, \ldots, a\} \]
Considerar\(g\) como una función de la fortuna inicial\(x\), para valores fijos de la probabilidad de victoria del juego\(p\) y la fortuna objetivo\(a\).
- \(g\)al principio aumenta y luego disminuye.
- \(g\)es cóncavo hacia abajo.
Cuando\( p = \frac{1}{2} \), el valor máximo de\( g \) es\( \frac{a^2}{4} \) y ocurre cuando\( x = \frac{a}{2} \). Cuando\(p \ne \frac{1}{2}\), el valor de\(x\) donde ocurre el máximo es bastante complicado.
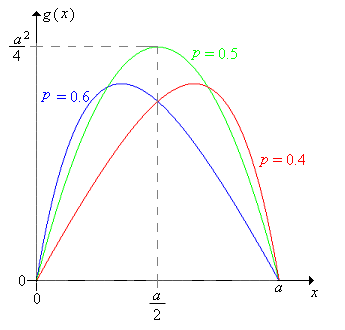
\(g\)es continuo en función de\(p\), para fijos\(x\) y\(a\).
Prueba
El valor esperado cuando\( p \ne \frac{1}{2} \) converge al valor esperado cuando\( p = \frac{1}{2} \), como\(p \to \frac{1}{2}\).
Para muchos ajustes de parámetros, el número esperado de juegos es sorprendentemente grande. Por ejemplo, supongamos eso\(p = \frac{1}{2}\) y la fortuna objetivo es 100. Si la fortuna inicial del jugador es 1, entonces el número esperado de juegos es 99, aunque la mitad del tiempo, el jugador se arruinará en el primer juego. Si la fortuna inicial es de 50, el número esperado de juegos es de 2500.
En el experimento rojo y negro, selecciona Timid Play. Varíe la fortuna inicial, la fortuna objetivo y la probabilidad de ganar el juego y observe cómo cambia el número esperado de juegos. Para diversos valores de los parámetros, ejecute el experimento 1000 veces y compare el número medio muestral de juegos con el valor esperado.
Incrementar la apuesta
¿Qué pasa si el jugador hace apuestas constantes, pero con una cantidad superior a 1? La respuesta a esta pregunta puede dar una idea de lo que sucederá con el juego audaz.
En el juego rojo y negro, fijó la fortuna objetivo en 16, la fortuna inicial en 8, y la probabilidad de victoria en 0.45. Juega 10 juegos con cada una de las siguientes estrategias. ¿Cuál parece funcionar mejor?
- Apuesta 1 en cada juego (jugada tímida).
- Apuesta 2 en cada juego.
- Apuesta 4 en cada juego.
- Apuesta 8 en cada juego (jugada negrita).
Habrá que embellecer nuestra notación para indicar la dependencia de la fortuna objetivo. Vamos\[ f(x, a) = \P(X_N = a \mid X_0 = x), \quad x \in \{0, 1, \ldots, a\}, \; a \in \N_+ \] Ahora arregle\(p\) y supongamos que la fortuna objetivo es\(2 a\) y la fortuna inicial es\(2 x\). Si el jugador juega tímidamente (apostando $1 cada vez), entonces por supuesto, su probabilidad de alcanzar el objetivo es\(f(2 x, 2 a)\). Por otro lado:
Supongamos que el jugador apuesta $2 en cada juego. El proceso de fortuna\((X_i / 2: i \in \N)\) corresponde a juego tímido con fortuna inicial\(x\) y fortuna objetivo\(a\) y que por lo tanto la probabilidad de que el jugador alcance el objetivo es\(f(x, a)\).
Por lo tanto, necesitamos comparar las probabilidades\(f(2 x, 2 a)\) y\(f(x, a)\).
Las funciones de probabilidad de ganancia están relacionadas de la siguiente manera:\[ f(2 x, 2 a) = f(x, a) \frac{(q / p)^x + 1}{(q / p)^a + 1}, \quad x \in \{0, 1, \ldots, a\} \] En particular
- \(f(2 x, 2 a) \lt f(x, a)\)si\(p \lt \frac{1}{2}\)
- \(f(2 x, 2 a) = f(x, a)\)si\(p = \frac{1}{2}\)
- \(f(2 x, 2 a) \gt f(x, a)\)si\(p \gt \frac{1}{2}\)
Así, parece que aumentar las apuestas es una buena idea si los juegos son injustos, una mala idea si los juegos son favorables, y no hace diferencia si los juegos son justos.
¿Y el número esperado de partidos jugados? Parece casi obvio que si se incrementan las apuestas, el número esperado de partidos jugados debería disminuir, pero un análisis directo usando la función de valor esperado anterior es más difícil de lo que uno podría esperar (¡pruébalo!) , Vamos a utilizar un método diferente, uno que realmente da mejores resultados. Específicamente, tendremos los jugadores de $1 y $2 apostando por la misma secuencia subyacente de juegos, para que los dos procesos de fortuna se definan en un mismo espacio de muestra. Entonces podemos comparar las variables aleatorias reales (el número de juegos jugados), lo que a su vez lleva a una comparación de sus valores esperados. Recordemos que a este método general se le conoce como acoplamiento.
Vamos a\(X_n\) denotar la fortuna después de los\(n\) juegos para la apuesta haciendo apuestas de $1 (simple juego tímido). Entonces\(2 X_n - X_0\) es la fortuna después de\(n\) juegos para el jugador haciendo apuestas de $2 (con la misma fortuna inicial, apostando por la misma secuencia de juegos). Asumir nuevamente que la fortuna inicial es\(2 x\) y la fortuna objetivo\(2 a\) donde\(0 \lt x \lt a\). Vamos a\(N_1\) denotar el número de juegos jugados por el jugador de $1, y\(N_2\) el número de juegos jugados por el jugador de $2, Entonces
- Si el jugador de $1 cae a la fortuna\(x\), el jugador de $2 se arruina (fortuna 0).
- Si el jugador de $1 golpea fortuna\(x + a\), el jugador de $2 alcanza el objetivo\(2 a\).
- El jugador de $1 debe golpear\(x\) antes de golpear 0 y debe golpear\(x + a\) antes de golpear\(2 a\).
- \(N_2 \lt N_1\)dado\(X_0 = 2 x\).
- \(\E(N_2 \mid X_0 = 2 x) \lt \E(N_1 \mid X_0 = 2 x)\)
Por supuesto, los valores esperados coinciden (y son ambos 0) si\(x = 0\) o\(x = a\). Este resultado muestra que\(N_2\) es estocásticamente más pequeño que\(N_1\) cuando los jugadores no están jugando la misma secuencia de juegos (de manera que las variables aleatorias no se definen en el mismo espacio de muestra).
Generalizar el análisis en esta subsección para comparar el juego tímido con la estrategia de apostar $\(k\) en cada juego (que sea la fortuna inicial\(k x\) y la fortuna objetivo\(k a\).
Parece que con juegos injustos, cuanto mayores sean las apuestas mejor, al menos en cuanto a la probabilidad de alcanzar el objetivo. Por lo tanto, naturalmente nos llevan a considerar el juego audaz.


