13.10: Juego en negrita
- Page ID
- 152130
Teoría Básica
Preliminares
Recordemos que con la estrategia del juego audaz en rojo y negro, el jugador de cada juego apuesta ya sea toda su fortuna o la cantidad necesaria para alcanzar la fortuna objetivo, la que sea menor. Como es habitual, nos interesa la probabilidad de que el jugador llegue al objetivo y el número esperado de pruebas. El primer dato interesante es que sólo importa la relación entre la fortuna inicial y la fortuna objetivo, bastante en contraste con el juego tímido.
Supongamos que el jugador juega audazmente con la fortuna inicial\(x\) y la fortuna objetivo\(a\). Como de costumbre, vamos a\(\bs{X} = (X_1, X_2, \ldots)\) denotar el proceso de la fortuna para el jugador. Para cualquiera\(c \gt 0\), el proceso aleatorio\(c \bs{X} = (c X_0, c X_1, \ldots)\) es el proceso de la fortuna para el juego audaz con la fortuna inicial\(c x\) y la fortuna objetivo\(c a\).
Debido a este resultado, es conveniente utilizar la fortuna objetivo como unidad monetaria y permitir fortunas iniciales irracionales, así como racionales. Así, el espacio de la fortuna es\([0, 1]\). A veces en nuestro análisis ignoraremos los estados 0 o 1; claramente no hay daño en esto porque en estos estados, el juego ha terminado.
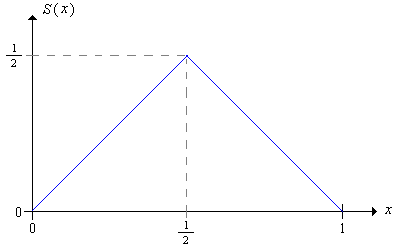
Recordemos que la función de apuestas\(S\) es la función que da la cantidad apostada en función de la fortuna actual. Para jugar en negrita, la función de apuestas es\[ S(x) = \min\{x, 1 - x\} = \begin{cases} x, & 0 \le x \le \frac{1}{2} \\ 1 - x, & \frac{1}{2} \le x \le 1 \end{cases} \]
La probabilidad de ganar
Denotaremos la probabilidad de que el jugador audaz alcance el objetivo a\(a = 1\) partir de la fortuna inicial\(x \in [0, 1]\) por\(F(x)\). Por la propiedad de escalado, la probabilidad de que el jugador en negrita alcance algún otro valor objetivo\(a \gt 0\), a partir de\(x \in [0, a]\) es\(F(x / a)\).
La función\(F\) satisface las siguientes condiciones de ecuación funcional y límite:
- \(F(x) = \begin{cases} p F(2 x), & 0 \le x \le \frac{1}{2}\\ p + q F(2 x - 1), & \frac{1}{2} \le x \le 1 \end{cases}\)
- \(F(0) = 0\),\(F(1) = 1\)
Del resultado anterior, y un poco de reflexión, debe quedar claro que un papel importante lo juega la siguiente función:
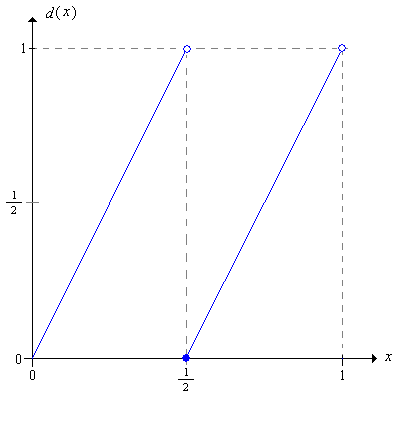
Dejar\(d\) ser la función definida\([0, 1)\) por\[ d(x) = 2 x - \lfloor 2 x \rfloor = \begin{cases} 2 x, & 0 \le x \lt \frac{1}{2} \\ 2 x - 1, & \frac{1}{2} \le x \lt 1 \end{cases} \] La función\(d\) se llama la función de duplicación, mod 1, ya que\(d(x)\) da la parte fraccionaria de\(2 x\).
Tenga en cuenta que hasta la última apuesta que termine el juego (con el jugador arruinado o victorioso), las sucesivas fortunas del jugador siguen iteraciones del mapa\(d\). Así, el juego audaz está íntimamente conectado con el sistema dinámico asociado con\(d\).
Expansiones Binarias
Una de las claves de nuestro análisis es representar la fortuna inicial en forma binaria.
La expansión binaria de\(x \in [0, 1)\) es\[ x = \sum_{i=1}^\infty \frac{x_i}{2^i} \] donde\(x_i \in \{0, 1\}\) para cada uno\(i \in \N_+\). Esta representación es única excepto cuando\(x\) es un racional binario (a veces también llamado racional diádico), es decir, un número de la forma\(k / 2^n\) donde\(n \in \N_+\) y\(k \in \{1, 3, \ldots, 2^n - 1\}\); el entero positivo\(n\) se llama el rango de\(x\). Los racionales binarios se discuten con más detalle en el capítulo sobre Fundaciones.
Para una racional binaria\(x\) de rango\(n\), usaremos la representación terminadora estándar donde\(x_n = 1\) y\(x_i = 0\) para\(i \gt n\). El rango se puede extender a todos los números en [0, 1) definiendo el rango de 0 para que sea 0 (0 también se considera un racional binario) y definiendo el rango de un binario irracional para ser\(\infty\). Denotaremos el rango de\(x\) by\(r(x)\).
Aplicada a las secuencias binarias, la función de duplicación\(d\) es el operador shift:
Para\(x \in [0, 1)\),\( [d(x)]_i = x_{i+1} \).
El juego audaz en rojo y negro se puede describir elegantemente comparando los bits de la fortuna inicial con los bits del juego.
Supongamos que el jugador comienza con la fortuna inicial\(x \in (0, 1)\). El jugador finalmente alcanza el objetivo 1 si y solo si existe un entero positivo\(k\) tal que\(I_j = 1 - x_j\) para\(j \in \{1, 2, \ldots, k - 1\}\) y\(I_k = x_k\). Es decir, el jugador gana si y sólo si cuando el bit del juego está de acuerdo con el bit de la fortuna correspondiente por primera vez, ese bit es 1.
La variable aleatoria cuyos bits son los complementos de los bits de la fortuna jugará un papel importante en nuestro análisis. Por lo tanto, vamos
\[ W = \sum_{j=1}^\infty \frac{1 - I_j}{2^j} \]
Tenga en cuenta que\(W\) es una variable aleatoria bien definida tomando valores en\([0, 1]\).
Supongamos que el jugador comienza con la fortuna inicial\(x \in (0, 1)\). Entonces el jugador alcanza el objetivo 1 si y sólo si\(W \lt x\).
Prueba
Esto se desprende del resultado anterior.
\(W\)tiene una distribución continua. Es decir,\(\P(W = x) = 0\) para cualquiera\(x \in [0, 1]\).
De los dos resultados anteriores, se deduce que\(F\) es simplemente la función de distribución de\(W\). En particular,\(F\) es una función creciente, y dado que\(W\) tiene una distribución continua,\(F\) es una función continua.
La función de éxito\(F\) es la solución continua única de la ecuación funcional anterior.
Prueba
La inducción en el rango muestra que dos soluciones cualesquiera deben estar de acuerdo en los racionales binarios. Pero entonces cualesquiera dos soluciones continuas deben estar de acuerdo para todos\(x \in [0, 1]\).
Si introducimos un poco más de notación, podemos dar buena expresión para\(F(x)\), y posteriormente para el número esperado de juegos\(G(x)\). Dejar\(p_0 = p\) y\(p_1 = q = 1 - p\).
La función de probabilidad de ganar se\(F\) puede expresar de la siguiente manera:\[ F(x) = \sum_{n=1}^\infty p_{x_1} \cdots p_{x_{n-1}} p x_n \]
Tenga\( p \cdot x_n \) en cuenta que en la última expresión es correcta; no es un error de impresión de\( p_{x_n} \). Así, en la suma sólo\( x_n = 1 \) se incluyen términos con.
\(F\)está aumentando estrictamente en\([0, 1]\). Esto significa que la distribución de\(W\) tiene soporte\([0, 1]\); es decir, no hay subintervalos de\([0, 1]\) que tengan longitud positiva, sino 0 probabilidad.
En particular,
- \(F\left(\frac{1}{8}\right) = p^3\)
- \(F\left(\frac{2}{8}\right) = p^2\)
- \(F\left(\frac{3}{8}\right) = p^2 + p^2 q\)
- \(F\left(\frac{4}{8}\right) = p\)
- \(F\left(\frac{5}{8}\right) = p + p^2 q\)
- \(F\left(\frac{6}{8}\right) = p + p q\)
- \(F\left(\frac{7}{8}\right) = p + p q + p q^2\)
Si\(p = \frac{1}{2}\) entonces\(F(x) = x\) por\(x \in [0, 1]\)
Prueba
Hay dos pruebas. La prueba más simple es señalar que\(x \mapsto x\) es continua y satisface la ecuación funcional en la ecuación funcional. Otra prueba se puede construir usando la representación de\( F \) como suma.
Así, para\(p = \frac{1}{2}\) (juicios justos), la probabilidad de que el jugador audaz alcance la fortuna objetivo a\(a\) partir de la fortuna inicial\(x\) es\(x / a\), tal como lo es para el jugador tímido. Tenga en cuenta también que la variable aleatoria\(W\) tiene la distribución uniforme encendida\([0, 1]\). Cuando\(p \ne \frac{1}{2}\), la distribución de\(W\) es bastante extraña. Para exponer el resultado de manera sucinta, indicaremos la dependencia de la de la medida de probabilidad\(\P\) sobre el parámetro\(p \in (0, 1)\). Primero definimos\[ C_p = \left\{ x \in [0, 1]: \frac{1}{n} \sum_{i=1}^n (1 - x_i) \to p \text{ as } n \to \infty \right\} \] Así,\(C_p\) es el conjunto de\(x \in [0, 1]\) para el cual es la frecuencia relativa de 0's en la expansión binaria\(p\).
Para distintos\(p, \, t \in (0, 1)\)
- \(\P_p(W \in C_p) = 1\)
- \(\P_p(W \in C_t) = 0\)
Prueba
La parte a) se desprende de la fuerte ley de los grandes números. La parte b) se desprende de la parte (a) ya que\(C_p \cap C_t = \emptyset\).
Cuando\(p \ne \frac{1}{2}\),\(W\) no tiene una función de densidad de probabilidad (con respecto a la medida de Lebesgue on [0, 1]), aunque\(W\) tenga una distribución continua.
Prueba
La prueba es por contradicción. Supongamos que\(W\) tiene función de densidad de probabilidad\(f\). Entonces\( 1 = \P_p(W \in C_p) = \int_{C_p} f(x) \, dx \). Pero si\( p \ne \frac{1}{2} \),\( \int_{C_p} 1 \, dx = \P_{1/2}(W \in C_p) = 0 \). Es decir,\(C_p\) tiene Lebesgue medida 0. Pero entonces\(\int_{C_p} f(x) \, dx = 0\), una contradicción.
Cuando\(p \ne \frac{1}{2}\),\(F\) tiene derivado 0 en casi todos los puntos de\([0, 1]\), a pesar de que está aumentando estrictamente.
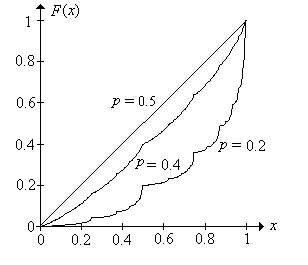
En el experimento rojo y negro, seleccione Bold Play. Varíe la fortuna inicial, la fortuna objetivo y la probabilidad de ganar el juego con las barras de desplazamiento y observe cómo cambia la probabilidad de ganar el juego. En particular, tenga en cuenta que esta probabilidad depende sólo de\(x / a\). Ahora, para varios valores de los parámetros, ejecute el experimento 1000 veces y compare la función de frecuencia relativa con la función de densidad de probabilidad.
El número esperado de juicios
Y\(G(x) = \E(N \mid X_0 = x)\) mucho\(x \in [0, 1]\), el número esperado de juicios a partir de las\(x\). Para cualquier otra fortuna objetivo\(a \gt 0\), el número esperado de pruebas a partir de las\(x \in [0, a]\) es justo\(G(x / a)\).
\(G\)satisface las siguientes condiciones de ecuación funcional y límite:
- \(G(x) = \begin{cases} 1 + p G(2 x), & 0 \lt x \le \frac{1}{2} \\ 1 + q G(2 x - 1), & \frac{1}{2} \le x \lt 1 \end{cases}\)
- \(G(0) = 0\),\(G(1) = 0\)
Prueba
La ecuación funcional se deriva del condicionamiento sobre el resultado del primer juego.
Obsérvese, curiosamente, que la ecuación funcional no se satisface en\(x = 0\) o\(x = 1\). Como antes, podemos dar un análisis alternativo utilizando la representación binaria de una fortuna inicial\(x \in (0, 1)\).
Supongamos que la fortuna inicial del jugador es\(x \in (0, 1)\). Entonces\(N = \min\{k \in \N_+: I_k = x_k \text{ or } k = r(x)\}\).
Prueba
Si\(x\) es un binario racional entonces\(N\) toma valores en el conjunto\(\{1, 2, \ldots, r(x)\}\). El juego continúa hasta que el número de juego concuerda con el rango de la fortuna o un bit de juego concuerda con el bit de fortuna correspondiente, el que sea más pequeño. En el primer caso, la penúltima fortuna es\(\frac{1}{2}\), la única fortuna para la que el próximo juego es siempre definitivo. Si\(x\) es un binario irracional entonces\(N\) toma valores adentro\(\N_+\). El juego continúa hasta que un poco de juego concuerda con un bit de fortuna correspondiente.
Podemos dar una fórmula explícita para el número esperado de ensayos\(G(x)\) en términos de la representación binaria de\(x\). Recordemos nuestra notación especial:\(p_0 = p\)\(p_1 = q = 1 - p\)
Supongamos que\(x \in (0, 1)\). Entonces\[ G(x) = \sum_{n=0}^{r(x) - 1} p_{x_1} \ldots p_{x_n} \]
Tenga en cuenta que el\(n = 0\) término es 1, ya que el producto está vacío. La suma tiene un número finito de términos si\(x\) es un binario racional, y la suma tiene un número infinito de términos si\(x\) es un binario irracional.
En particular,
- \(G\left(\frac{1}{8}\right) = 1 + p + p^2\)
- \(G\left(\frac{2}{8}\right) = 1 + p\)
- \(G\left(\frac{3}{8}\right) = 1 + p + p q\)
- \(G\left(\frac{4}{8}\right) = 1\)
- \(G\left(\frac{5}{8}\right) = 1 + q + p q\)
- \(G\left(\frac{6}{8}\right) = 1 + q\)
- \(G\left(\frac{7}{8}\right) = 1 + q + q^2\)
Si\(p = \frac{1}{2}\) entonces
\[ G(x) = \begin{cases} 2 - \frac{1}{2^{r(x) - 1}}, & x \text{ is a binary rational} \\ 2, & x \text{ is a binary irrational} \end{cases} \]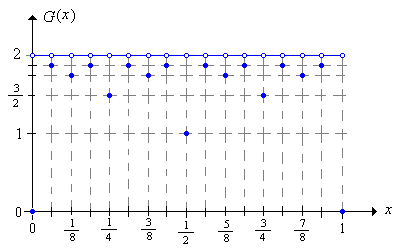
En el experimento rojo y negro, seleccione Bold Play. Varíe\(x\)\(a\),, y\(p\) con las barras de desplazamiento y anote cómo cambia el número esperado de ensayos. En particular, tenga en cuenta que la media depende únicamente de la relación\(x / a\). Para valores seleccionados de los parámetros, ejecute el experimento 1000 veces y compare la media de la muestra con la media de distribución.
Para fijo\(x\),\(G\) es continuo en función de\(p\).
No obstante, en función de la fortuna inicial\(x\), para fijo\(p\), la función\(G\) es muy irregular.
\(G\)es discontinuo en los racionales binarios en\([0, 1]\) y continuo en los irracionales binarios.


