15.1: Introducción
- Page ID
- 152148
Un proceso de renovación es un modelo estocástico idealizado para eventos
que ocurren aleatoriamente en el tiempo. Estos eventos temporales se denominan genéricamente renovaciones o llegadas. Aquí hay algunas interpretaciones y aplicaciones típicas.
- Las llegadas son
clientes
que llegan a unaestación de servicio
. Nuevamente, los términos son genéricos. Un cliente puede ser una persona y la estación de servicio una tienda, pero también un cliente puede ser una solicitud de archivo y la estación de servicio un servidor web. - Un dispositivo se pone en servicio y finalmente falla. Se sustituye por un dispositivo del mismo tipo y se repite el proceso. No contamos el tiempo de reemplazo en nuestro análisis; equivalentemente podemos asumir que el reemplazo es inmediato. Los tiempos de los reemplazos son las renovaciones
- Las llegadas son tiempos de algún acontecimiento natural, como un rayo, un tornado o un terremoto, en un punto geográfico determinado.
- Las llegadas son emisiones de partículas elementales de una fuente radiactiva.
Procesos Básicos
El modelo básico en realidad da lugar a varios procesos aleatorios interrelacionados: la secuencia de tiempos entre llegadas, la secuencia de tiempos de llegada y el proceso de conteo. El proceso de renovación del término puede referirse a cualquiera (o a todos) de estos. También se presentan varios procesos de la edad
natural que surgen. En esta sección definiremos y estudiaremos las propiedades básicas de cada uno de estos procesos a su vez.
Horarios Interarrival
Dejar\(X_1\) denotar la hora de la primera llegada, y\(X_i\) el tiempo entre las llegadas\((i - 1)\) st y\(i\) th para\(i \in \{2, 3, \ldots)\). Nuestra suposición básica es que la secuencia de tiempos de interllegada\(\bs{X} = (X_1, X_2, \ldots)\) es una secuencia independiente, idéntica distribuida de variables aleatorias. En términos estadísticos,\(\bs{X}\) corresponde al muestreo a partir de la distribución de un tiempo genérico entre llegadas\(X\). Suponemos que\(X\) toma valores en\([0, \infty)\) y\(\P(X \gt 0) \gt 0\), de manera que los tiempos de interllegada son no negativos, pero no idénticamente 0. Vamos a\(\mu = \E(X)\) denotar la media común de los tiempos interarribos. Permitimos esa posibilidad eso\(\mu = \infty\). Por otra parte,
\(\mu \gt 0\).
Prueba
Este es un dato básico a partir de propiedades de valor esperado. Para una simple prueba, tenga en cuenta que si\(\mu = 0\) entonces\(\P(X \gt x) = 0\) por cada\(x \gt 0\) por la desigualdad de Markov. Pero entonces\(\P(X = 0) = 1\).
Si\(\mu \lt \infty\), vamos a dejar\(\sigma^2 = \var(X)\) denotar la varianza común de los tiempos interarribos. Dejar\(F\) denotar la función común de distribución de los tiempos de interllegada, para que\[ F(x) = \P(X \le x), \quad x \in [0, \infty) \] La función de distribución\(F\) resulte ser de fundamental importancia en el estudio de los procesos de renovación. Dejaremos\(f\) denotar la función de densidad de probabilidad de los tiempos entre llegadas si la distribución es discreta o si la distribución es continua y tiene una función de densidad de probabilidad (es decir, si la distribución es absolutamente continua con respecto a la medida de Lebesgue on\( [0, \infty) \)). En el caso discreto, resulta importante la siguiente definición:
Si\( X \) toma valores en el conjunto\( \{n d: n \in \N\} \) para algunos\( d \in (0, \infty) \), entonces\( X \) (o su distribución) se dice que es aritmética (también se utilizan los términos celosía y periódico). El más grande de tales\( d \) es el lapso de\( X \).
La razón por la que la definición es importante es porque el comportamiento limitante de los procesos de renovación resulta ser más complicado cuando la distribución entre llegadas es aritmética.
Los tiempos de llegada
Vamos\[ T_n = \sum_{i=1}^n X_i, \quad n \in \N \] Seguimos nuestra convención habitual de que la suma sobre un conjunto de índices vacíos es 0; así\(T_0 = 0\). Por otro lado,\(T_n\) es la hora de la llegada\(n\) th para\(n \in \N_+\). A la secuencia\(\bs{T} = (T_0, T_1, \ldots)\) se le llama proceso de tiempo de llegada, aunque tenga en cuenta que no\(T_0\) se considera una llegada. Un proceso de renovación se llama así porque el proceso comienza de nuevo, independientemente del pasado, en cada hora de llegada.
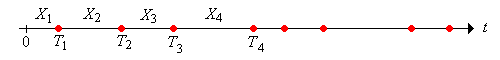
La secuencia\(\bs{T}\) es el proceso de suma parcial asociado con la secuencia independiente, idénticamente distribuida de tiempos de interllegada\(\bs{X}\). Los procesos de suma parcial asociados a secuencias independientes, distribuidas idénticamente, han sido estudiados en varios lugares de este proyecto. En lo que resta de esta subsección, recopilaremos algunos de los datos más importantes sobre dichos procesos. Primero, podemos recuperar los tiempos de interllegada a partir de los tiempos de llegada:\[ X_i = T_i - T_{i-1}, \quad i \in \N_+ \] A continuación, vamos a\(F_n\) denotar la función de distribución de\(T_n\), de manera que\[ F_n(t) = \P(T_n \le t), \quad t \in [0, \infty) \] Recordemos que si\(X\) tiene función de densidad de probabilidad\(f\) (ya sea en el caso discreto o continuo), entonces\(T_n\) tiene función de densidad de probabilidad\(f_n = f^{*n} = f * f * \cdots * f\), el poder de convolución\(n\) -fold de\(f\).
La secuencia de tiempos de llegada\(\bs{T}\) tiene incrementos estacionarios e independientes:
- Si\(m \le n\) entonces\(T_n - T_m\) tiene la misma distribución que\(T_{n-m}\) y por lo tanto tiene función de distribución\(F_{n-m}\)
- Si\(n_1 \le n_2 \le n_3 \le \cdots\) entonces\(\left(T_{n_1}, T_{n_2} - T_{n_1}, T_{n_3} - T_{n_2}, \ldots\right)\) es una secuencia de variables aleatorias independientes.
Prueba
Recordemos que estas son propiedades que se mantienen generalmente para la secuencia de suma parcial asociada a una secuencia de variables IID.
Si\(n, \, m \in \N\) entonces
- \(\E\left(T_n\right) = n \mu\)
- \(\var\left(T_n\right) = n \sigma^2\)
- \(\cov\left(T_m, T_n\right) = \min\{m,n\} \sigma^2\)
Prueba
La parte (a) sigue, por supuesto, de la propiedad aditiva del valor esperado, y la parte (b) de la propiedad aditiva de varianza para sumas de variables independientes. Para la parte c), supongamos que\(m \le n\). Entonces\(T_n = T_m + (T_n - T_m)\). Pero\(T_m\) y\(T_n - T_m\) son independientes, entonces\[ \cov\left(T_m, T_n\right) = \cov\left[T_m, T_m + (T_n - T_m)\right] = \cov(T_m, T_m) + \cov(T_m, T_n - T_m) = \var(T_m) = m \sigma^2 \]
Recordemos la ley de los grandes números:\(T_n / n \to \mu\) como\(n \to \infty\)
- Con probabilidad 1 (la ley fuerte).
- En probabilidad (la ley débil).
Tenga en cuenta que\(T_n \le T_{n+1}\) para\(n \in \N\) ya que los tiempos interarribos no son negativos. También\(\P(T_n = T_{n-1}) = \P(X_n = 0) = F(0)\). Esto puede ser positivo, por lo que con probabilidad positiva, más de una llegada puede ocurrir al mismo tiempo. Por otro lado, los horarios de llegada no tienen límites:
\(T_n \to \infty\)como\(n \to \infty\) con probabilidad 1.
Prueba
Ya que\(\P(X \gt 0) \gt 0\), hay salidas de\(t \gt 0\) tal manera que\(\P(X \gt t) \gt 0\). Del segundo lema de Borel-Cantelli se deduce que con probabilidad 1,\(X_i \gt t\) para infinitamente muchos\(n \in \N_+\). Por lo tanto\(\sum_{i=1}^\infty X_i = \infty\) con probabilidad 1.
El proceso de conteo
Para\(t \ge 0\), vamos a\(N_t\) denotar el número de llegadas en el intervalo\([0, t]\):\[ N_t = \sum_{n=1}^\infty \bs{1}(T_n \le t), \quad t \in [0, \infty) \] Nos referiremos al proceso aleatorio\(\bs{N} = (N_t: t \ge 0)\) como el proceso de conteo. Recordemos nuevamente que no\( T_0 = 0 \) se considera una llegada, pero es posible tener\( T_n = 0 \) para\( n \in \N_+ \), por lo que puede haber una o más llegadas a la hora 0.
\(N_t = \max\{n \in \N: T_n \le t\}\)para\(t \ge 0\).
Si\(s, \, t \in [0, \infty)\) y\(s \le t\) entonces\(N_t - N_s\) es el número de llegadas en\((s, t]\).
Tenga en cuenta que en función de\(t\),\(N_t\) es una función de paso (aleatoria) con saltos en los distintos valores de\((T_1, T_2, \ldots)\); el tamaño del salto en una hora de llegada es el número de llegadas en ese momento. En particular,\(N\) es una función cada vez mayor de\(t\).
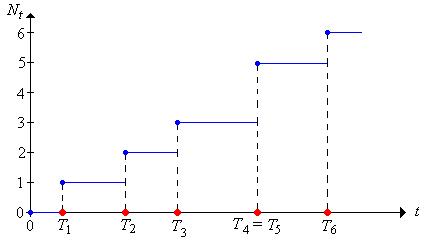
De manera más general, podemos definir la medida de conteo (aleatoria) correspondiente a la secuencia de puntos aleatorios\((T_1, T_2, \ldots)\) en\([0, \infty)\). Así, si\(A\) es un subconjunto (medible) de\([0, \infty)\), vamos a dejar\(N(A)\) denotar el número de los puntos aleatorios en\(A\):\[ N(A) = \sum_{n=1}^\infty \bs{1}(T_n \in A) \] En particular, tenga en cuenta que con nuestra nueva notación,\(N_t = N[0, t]\) para\(t \ge 0\) y\(N(s, t] = N_t - N_s\) para\(s \le t\). Así, la medida de conteo aleatorio está completamente determinada por el proceso de conteo. El proceso de conteo es la función de medida acumulativa
para la medida de conteo, análoga a la función de distribución acumulativa de una medida de probabilidad.
Para\(t \ge 0\) y\(n \in \N\),
- \(T_n \le t\)si y solo si\(N_t \ge n\)
- \(N_t = n\)si y solo si\(T_n \le t \lt T_{n+1}\)
Prueba
Tenga en cuenta que el evento en la parte (a) significa que al menos hay\(n\) llegadas en\([0, t]\). El evento en la parte (b) significa que hay exactamente\(n\) llegadas en\([0, t]\).
Por supuesto, los complementos de los eventos en (a) también son equivalentes, así que\( T_n \gt t \) si y sólo si\( N_t \lt n \). Por otra parte, ninguno de los acontecimientos\( N_t \le n \) e\( T_n \ge t \) implica el otro. Por ejemplo, couse fácilmente tener\( N_t = n \) y\( T_n \lt t \lt T_{n + 1} \). Tomando complementos, ninguno de los eventos\( N_t \gt n \) e\( T_n \lt t \) implica el otro. El último resultado también muestra que el proceso de tiempo de llegada\( \bs{T} \) y el proceso de conteo\( \bs{N} \) son inversos el uno del otro en cierto sentido.
Los siguientes eventos tienen probabilidad 1:
- \(N_t \lt \infty\)para todos\( t \in [0, \infty) \)
- \(N_t \to \infty\)como\(t \to \infty\)
Prueba
El suceso en la parte (a) ocurre si y sólo si\(T_n \to \infty\) como\(n \to \infty\), lo que ocurre con probabilidad 1 por el resultado anterior. El suceso en la parte (b) ocurre si y sólo si\(T_n \lt \infty\) para todos\(n \in \N\) lo cual también ocurre con probabilidad 1.
Todos los resultados hasta el momento de esta subsección muestran que el proceso de tiempo de llegada\(\bs{T}\) y el proceso de conteo\(\bs{N}\) son inversos el uno del otro en cierto sentido. Las equivalencias importantes anteriores pueden ser utilizadas para obtener la distribución de probabilidad de las variables de conteo en términos de la función de distribución entre llegadas\(F\).
Para\(t \ge 0\) y\(n \in \N\),
- \(\P(N_t \ge n) = F_n(t)\)
- \(\P(N_t = n) = F_n(t) - F_{n+1}(t)\)
El siguiente resultado es poco más que una reexpresión del resultado anterior relacionando el proceso de conteo y el proceso de tiempo de llegada. Sin embargo, es posible que deba revisar la sección sobre filtraciones y tiempos de parada para comprender el resultado
Para\( t \in [0, \infty) \),\( N_t + 1 \) es un tiempo de parada para la secuencia de tiempos entre llegadas\( \bs{X} \)
Prueba
Tenga en cuenta que\( N_t + 1 \) toma valores en\( \N_+ \), por lo que necesitamos demostrar que el evento\( \left\{N_t + 1 = n\right\} \) es medible con respecto a\( \mathscr{F}_n = \sigma\{X_1, X_2, \ldots, X_n\} \) for\( n \in \N_+ \). Pero del resultado anterior,\( N_t + 1 = n \) si y solo si y solo\( N_t = n - 1 \) si y solo si\( T_{n-1} \le t \lt T_n \). El último evento es claramente medible con respecto a\( \mathscr{F}_n \).
La función de renovación
La función\( M \) que da el número esperado de llegadas hasta el momento\(t\) se conoce como la función de renovación:\[ M(t) = \E(N_t), \quad t \in [0, \infty) \]
La función de renovación resulta de fundamental importancia en el estudio de los procesos de renovación. En efecto, la función de renovación caracteriza esencialmente el proceso de renovación. Tomará un tiempo entender esto completamente, pero el siguiente teorema es un primer paso:
La función de renovación se da en términos de la función de distribución entre llegadas por\[ M(t) = \sum_{n=1}^\infty F_n(t), \quad 0 \le t \lt \infty \]
Prueba
Recordemos eso\(N_t = \sum_{n=1}^\infty \bs{1}(T_n \le t)\). Tomar valores esperados da el resultado. Tenga en cuenta que el intercambio de suma y valor esperado es válido porque los términos no son negativos.
Tenga en cuenta que aún no hemos demostrado eso\(M(t) \lt \infty\) para\(t \ge 0\), y señalar también que esto no se desprende del teorema anterior. Sin embargo, estableceremos esta condición de finitud en la subsección sobre el momento generando funciones a continuación. Si\( M \) es diferenciable, a la derivada\( m = M^\prime \) se le conoce como la densidad de renovación, por lo que\( m(t) \) da la tasa esperada de llegadas por unidad de tiempo a\( t \in [0, \infty) \).
De manera más general, si\(A\) es un subconjunto (medible) de\([0, \infty)\), let\(M(A) = \E[N(A)]\), el número esperado de llegadas en\(A\).
\(M\)es una medida positiva sobre\([0, \infty)\). A esta medida se le conoce como la medida de renovación.
Prueba
\(N\)es una medida sobre\([0, \infty)\) (aunque aleatoria). Entonces si\((A_1, A_2, \ldots)\) es una secuencia de subconjuntos disjuntos, medibles de\([0, \infty)\) entonces\[ N\left(\bigcup_{i=1}^\infty A_i \right) = \sum_{i=1}^\infty N(A_i) \] Tomando valores esperados da\[ m\left(\bigcup_{i=1}^\infty A_i \right) = \sum_{i=1}^\infty m(A_i) \] De nuevo, el intercambio de suma y valor esperado se justifica ya que los términos son no negativos.
La medida de renovación también viene dada por\[ M(A) = \sum_{n=1}^\infty \P(T_n \in A), \quad A \subset [0, \infty) \]
Prueba
Recordemos eso\(N(A) = \sum_{n=1}^\infty \bs{1}(T_n \in A)\). Tomar valores esperados da el resultado. Nuevamente, se justifica el intercambio de valor esperado y series infinitas ya que los términos no son negativos.
Si\( s\, \, t \in [0, \infty) \) con\(s \le t\) entonces\(M(t) - M(s) = m(s, t]\), el número esperado de llegadas en\((s, t]\).
El último teorema implica que la función de renovación determina realmente toda la medida de renovación. La función de renovación es la función de medida acumulativa
, análoga a la función de distribución acumulativa de una medida de probabilidad. Así, cada proceso de renovación conduce naturalmente a dos medidas sobre\([0, \infty)\), la medida de conteo aleatorio correspondiente a los tiempos de llegada, y la medida asociada con el número esperado de llegadas.
Los procesos de la era
Para\(t \in [0, \infty)\),\(T_{N_t} \le t \lt T_{N_t + 1}\). Es decir,\(t\) está en el intervalo aleatorio de renovación\([T_{N_t}, T_{N_t + 1})\).
Considere la configuración de confiabilidad en la que cada vez que falla un dispositivo, se reemplaza inmediatamente por un nuevo dispositivo del mismo tipo. Entonces la secuencia de tiempos de interllegada\(\bs{X}\) es la secuencia de vidas, mientras que\(T_n\) es el tiempo en que el dispositivo\(n\) th se pone en servicio. Hay varios otros procesos aleatorios naturales que se pueden definir.
La variable aleatoria\[ C_t = t - T_{N_t}, \quad t \in [0, \infty) \] se llama la vida actual en el tiempo\(t\). Esta variable toma valores en el intervalo\([0, t]\) y es la antigüedad del dispositivo que está en servicio en el momento\(t\). El proceso aleatorio\(\bs{C} = (C_t: t \ge 0)\) es el proceso de vida actual.
La variable aleatoria\[ R_t = T_{N_t + 1} - t, \quad t \in [0, \infty) \] se llama la vida restante en el tiempo\(t\). Esta variable toma valores en el intervalo\((0, \infty)\) y es el tiempo restante hasta que\(t\) falla el dispositivo que está en servicio en el momento. El proceso aleatorio\(\bs{R} = (R_t: t \ge 0)\) es el proceso de vida restante.
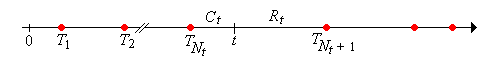
La variable aleatoria\[ L_t = C_t + R_t = T_{N_t+1} - T_{N_t} = X_{N_t + 1}, \quad t \in [0, \infty) \] se llama la vida total en el tiempo\(t\). Esta variable toma valores\([0, \infty)\) y da la vida total del dispositivo que está en servicio en el momento\(t\). El proceso aleatorio\(\bs{L} = (L_t: t \ge 0)\) es el proceso de vida total.
Los eventos de cola de la vida actual y restante pueden escribirse en términos unos de otros y en términos de las variables de conteo.
Supongamos que\(t \in [0, \infty)\)\(x \in [0, t]\),, y\(y \in [0, \infty)\). Entonces
- \(\{R_t \gt y\} = \{N_{t+y} - N_t = 0\}\)
- \(\{C_t \ge x \} = \{R_{t-x} \gt x\} = \{N_t - N_{t-x} = 0\}\)
- \(\{C_t \ge x, R_t \gt y\} = \{R_{t-x} \gt x + y\} = \{N_{t+y} - N_{t-x} = 0\}\)
Prueba
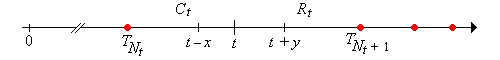
Por supuesto, los diversos eventos equivalentes en el último resultado deben tener la misma probabilidad. En particular, se deduce que si conocemos la distribución de\(R_t\) para todos\(t\) entonces también conocemos la distribución de\(C_t\) para todos\(t\), y de hecho conocemos la distribución conjunta de\( (R_t, C_t) \) para todos\(t\) y de ahí también la distribución de\(L_t\) para todos\(t\).
Para fijo,\( t \in (0, \infty) \) la vida total en\( t \) (la vida útil del dispositivo en servicio en el momento\( t \)) es estocásticamente mayor que una vida útil genérica. Este resultado, un poco sorprendente al principio, se conoce como la paradoja de la inspección. Dejar\( X \) denotar tiempo fijo entre llegadas.
\( \P(L_t \gt x) \ge \P(X \gt x) \)para\( x \ge 0 \).
Prueba
Recordemos eso\( L_t = X_{N_t + 1} \). El comprobante es por condicionamiento\( N_t \). Una herramienta importante es el hecho de que si\( A \) y\( B \) son eventos anidados en un espacio de probabilidad (uno un subconjunto del otro), entonces los eventos están correlacionados positivamente, de manera que eso\( \P(A \mid B) \ge \P(A) \). Recordemos que\( F \) es el CDF común de los tiempos interarribos. Primero\[ \P\left(X_{N_t + 1} \gt x \mid N_t = 0\right) = \P(X_1 \gt x \mid X_1 \gt t) \ge \P(X_1 \gt x) = 1 - F(x) \] Siguiente, para\( n \in \N_+ \),\[ \P\left(X_{N_t + 1} \gt x \mid N_t = n\right) = \P\left(X_{n + 1} \gt x \mid T_n \le t \lt T_{n + 1}\right) = \P(X_{n+1} \gt x \mid T_n \le t \lt T_n + X_{n+1}) \] Acondicionamos esto adicionalmente en\( T_n \), la hora de la llegada\( n \) th. Porque\( s \le t \), y ya que\( X_{n+1} \) es independiente de\( T_n \), tenemos De\[ \P(X_{n+1} \gt x \mid T_n = s, \, X_{n+1} \gt t - s) = \P(X_{n+1} \gt x \mid X_{n + 1} \gt t - s) \ge \P(X_{n + 1} \gt x) = 1 - F(x) \] ello se deduce que\( \P\left(X_{N_t + 1} \gt x \mid N_t = n\right) \ge 1 - F(x) \) para cada\( n \in \N \), y por lo tanto\[ \P\left(X_{N_t + 1} \gt x\right) = \sum_{n=0}^\infty \P\left(X_{N_t + 1} \gt x \mid N_t = n\right) \P(N_t = n) \ge \sum_{n=0}^\infty \left[1 - F(x)\right] \P(N_n = n) = 1 - F(x) \]
Comparación básica
La comparación básica en el siguiente resultado suele ser útil, particularmente para obtener diversos límites. La idea es muy simple: si se acortan los tiempos de interllegada, las llegadas ocurren con mayor frecuencia.
Supongamos ahora que tenemos dos secuencias entre llegadas,\(\bs{X} = (X_1, X_2, \ldots)\) y\(\bs{Y} = (Y_1, Y_2, \ldots)\) definidas en el mismo espacio de probabilidad, con\(Y_i \le X_i\) (con probabilidad 1) para cada una\(i\). Entonces para\(n \in \N\) y\(t \in [0, \infty)\),
- \(T_{Y,n} \le T_{X,n}\)
- \(N_{Y,t} \ge N_{X,t}\)
- \(m_Y(t) \ge m_X(t)\)
Ejemplos y Casos Especiales
Juicios de Bernoulli
Supongamos que\( \bs{X} = (X_1, X_2, \ldots) \) es una secuencia de ensayos de Bernoulli con parámetro de éxito\(p \in (0, 1)\). Recordemos que\(\bs{X}\) es una secuencia de variables indicadoras independientes, distribuidas idénticamente con\(\P(X = 1) = p\).
Recordemos los procesos aleatorios derivados de\(\bs{X}\):
- \(\bs{Y} = (Y_0, Y_1, \ldots)\)donde\(Y_n\) el número de éxitos en los primeros\(n\) juicios. La secuencia\(\bs{Y}\) es el proceso de suma parcial asociado con\(\bs{X}\). La variable\(Y_n\) tiene la distribución binomial con parámetros\(n\) y\(p\).
- \(\bs{U} = (U_1, U_2, \ldots)\)donde\(U_n\) el número de ensayos necesarios para pasar del número de éxito\(n - 1\) al número de éxito\(n\). Se trata de variables independientes, cada una con la distribución geométrica\( \N_+ \) con parámetro\(p\).
- \(\bs{V} = (V_0, V_1, \ldots)\)donde\(V_n\) está el número de prueba de éxito\(n\). La secuencia\(\bs{V}\) es el proceso de suma parcial asociado con\(\bs{U}\). La variable\(V_n\) tiene la distribución binomial negativa con parámetros\(n\) y\(p\).
Es natural ver los éxitos como llegadas en un proceso de renovación de tiempo discreto.
Considera el proceso de renovación con secuencia entre llegadas\(\bs{U}\). Entonces
- Se satisfacen los supuestos básicos y que el tiempo medio entre llegadas es\(\mu = 1 / p\).
- \(\bs{V}\)es la secuencia de los tiempos de llegada.
- \(\bs{Y}\)es el proceso de conteo (restringido a\(\N\)).
- La función de renovación es\(m(n) = n p\) para\(n \in \N\).
De ello se deduce que la medida de renovación es proporcional a la medida contabilizada\(\N_+\).
Ejecutar el experimento de línea de tiempo binomial 1000 veces para diversos valores de los parámetros\(n\) y\(p\). Comparar la distribución empírica de la variable de conteo con la distribución verdadera.
Ejecutar el experimento binomial negativo 1000 veces para diversos valores de los parámetros\(k\) y\(p\). Comare la distribución empírica del tiempo de llegada a la distribución verdadera.
Consideremos nuevamente el proceso de renovación con secuencia entre llegadas\(\bs{U}\). Para\(n \in \N\),
- La vida actual y la vida restante en el momento\(n\) son independientes.
- La vida restante en el tiempo\(n\) tiene la misma distribución que un tiempo interllegada\(U\), es decir, la distribución geométrica on\( \N_+ \) con parámetro\(p\).
- La vida actual en el tiempo\(n\) tiene una distribución geométrica truncada con parámetros\(n\) y\(p\):\[ \P(C_n = k) = \begin{cases} p(1 - p)^k, & k \in \{0, 1, \ldots, n - 1\} \\ (1 - p)^n, & k = n \end{cases} \]
Prueba
Estos resultados se derivan de los eventos anteriores del proceso de edad.
Este proceso de renovación comienza de nuevo, independientemente del pasado, no sólo en los horarios de llegada, sino\(n \in \N\) también en horarios fijos. El proceso de ensayos de Bernoulli (con los éxitos como llegadas) es el único proceso de renovación de tiempo discreto con esta propiedad, lo que es consecuencia de la propiedad sin memoria de la distribución geométrica entre llegadas.
También podemos usar las variables indicadoras como los tiempos entre llegadas. Esto puede parecer extraño al principio, pero en realidad resulta útil.
Considera el proceso de renovación con secuencia entre llegadas\(\bs{X}\).
- Se satisfacen los supuestos básicos y que el tiempo medio entre llegadas es\(\mu = p\).
- \(\bs{Y}\)es la secuencia de los tiempos de llegada.
- El número de llegadas al tiempo 0 es\(U_1 - 1\) y el número de llegadas al momento\(i \in \N_+\) es\(U_{i+1}\).
- El número de llegadas en el intervalo\([0, n]\) es\(V_{n+1} - 1\) para\(n \in \N\). Esto da el proceso de conteo.
- La función de renovación es\(m(n) = \frac{n + 1}{p} - 1\) para\(n \in \N\).
Los procesos de edad no son muy interesantes para este proceso de renovación.
Para\(n \in \N\) (con probabilidad 1),
- \(C_n = 0\)
- \(R_n = 1\)
La función generadora de momento de las variables de conteo
Como aplicación del último proceso de renovación, podemos demostrar que la función de generación de momento de la variable de conteo\(N_t\) en un proceso de renovación arbitraria es finita en un intervalo de aproximadamente 0 para cada\(t \in [0, \infty)\). Esto implica que\(N_t\) tiene momentos finitos de todos los órdenes y en particular eso\(m(t) \lt \infty\) para cada uno\(t \in [0, \infty)\).
Supongamos que esa\(\bs{X} = (X_1, X_2, \ldots)\) es la secuencia entre llegadas para un proceso de renovación. Por los supuestos básicos, existe\(a \gt 0\) tal que\(p = \P(X \ge a) \gt 0\). Consideramos ahora el proceso de renovación con secuencia entre llegadas\(\bs{X}_a = (X_{a,1}, X_{a,2}, \ldots)\), donde\(X_{a,i} = a\,\bs{1}(X_i \ge a)\) para\(i \in \N_+\). El proceso de renovación con secuencia interllegada\(\bs{X}_a\) es igual que el proceso de renovación con interllegadas de Bernoulli, excepto que los tiempos de llegada ocurren en los puntos de la secuencia\((0, a, 2 a, \ldots)\), en lugar de\( (0, 1, 2, \ldots) \).
Para cada uno\(t \in [0, \infty)\),\(N_t\) tiene función de generación de momento finito en un intervalo de aproximadamente 0, y por lo tanto\( N_t \) tiene momentos de todos los órdenes a 0.
Prueba
Tenga en cuenta primero que\(X_{a,i} \le X_i\) para cada uno\(i \in \N_+\). Recordemos el momento generando función\(\Gamma\) de la distribución geométrica con parámetro\(p\) es\[ \Gamma(s) = \frac{e^s p}{1 - (1 - p) e^s}, \quad s \lt -\ln(1 - p) \] Pero al igual que con el proceso con tiempos de interllegada de Bernoulli, se\(N_{a,t}\) puede escribir como\(a (V_{n + 1} - 1)\) donde\(n = \lfloor a / t \rfloor\) y donde\(V_{n + 1}\) es una suma de\(n + 1\) IID variables geométricas, cada una con parámetro\(p\). Realmente no nos importa la forma explícita del MGF de\(N_{a, t}\), pero es claramente finita en un intervalo del desde\((-\infty, \epsilon)\) donde\(\epsilon \gt 0\). Pero\(N_t \le N_{t,a}\), por lo que su MGF también es finito en este intervalo.
El proceso de Poisson
El proceso de Poisson, llamado así por Simeon Poisson, es el más importante de todos los procesos de renovación. El proceso de Poisson es tan importante que se trata en un capítulo separado en este proyecto. Por favor revise las propiedades esenciales de este proceso:
Propiedades del proceso de Poisson con tasa\( r \in (0, \infty) \).
- Los tiempos interllegados tienen una distribución exponencial con parámetro de tasa\(r\). Así, se satisfacen los supuestos básicos anteriores y el tiempo medio entre llegadas lo es\(\mu = 1 / r\).
- La distribución exponencial es la única distribución con la propiedad sin memoria en\([0, \infty)\).
- El tiempo de la llegada\(n\) th\(T_n\) tiene la distribución gamma con el parámetro shape\(n\) y el parámetro rate\(r\).
- El proceso de conteo\(\bs{N} = (N_t: t \ge 0)\) tiene incrementos estacionarios e independientes y\(N_t\) tiene la distribución de Poisson con parámetro\(r t\) para\(t \in [0, \infty)\).
- En particular, la función de renovación es\(m(t) = r t\) para\(t \in [0, \infty)\). Por lo tanto, la medida de renovación es un múltiplo de la medida de longitud estándar (medida Lebesgue) en\([0, \infty)\).
Consideremos nuevamente el proceso de Poisson con parámetro de tasa\(r\). Para\(t \in [0, \infty)\),
- La vida actual y la vida restante en el momento\(t\) son independientes.
- La vida restante en el tiempo\(t\) tiene la misma distribución que un tiempo interllegada\(X\), es decir, la distribución exponencial con parámetro de tasa\(r\).
- La vida actual en el tiempo\(t\) tiene una distribución exponencial truncada con parámetros\(t\) y\(r\):\[ \P(C_t \ge s) = \begin{cases} e^{-r s}, & 0 \le s \le t \\ 0, & s \gt t \end{cases} \]
Prueba
Estos resultados se derivan de los eventos del proceso de edad dados anteriormente.
El proceso de Poisson comienza de nuevo, independientemente del pasado, no sólo en los horarios de llegada, sino\(t \in [0, \infty)\) también en horarios fijos. El proceso de Poisson es el único proceso de renovación con esta propiedad, que es consecuencia de la propiedad sin memoria de la distribución exponencial interllegada.
Ejecutar el experimento de Poisson 1000 veces para diversos valores de los parámetros\(t\) y\(r\). Comparar la distribución empírica de la variable de conteo con la distribución verdadera.
Ejecutar el experimento gamma 1000 veces para diversos valores de los parámetros\(n\) y\(r\). Comparar la distribución empírica del tiempo de llegada con la distribución verdadera.
Ejercicios de simulación
Abre el experimento de renovación y establece\( t = 10 \). Para cada una de las siguientes distribuciones interllegadas, ejecute la simulación 1000 veces y anote la forma y ubicación de la distribución empírica de la variable de conteo. Obsérvese también la media de la distribución entre llegadas en cada caso.
- La distribución uniforme continua en el intervalo\( [0, 1] \) (la distribución uniforme estándar).
- la distribución uniforme discreta a partir de\( a = 0 \), con tamaño\( h = 0.1 \) de paso y con\( n = 10 \) puntos.
- La distribución gamma con parámetro de forma\( k = 2 \) y parámetro de escala\( b = 1 \).
- La distribución beta con parámetro de forma izquierda\( a = 3 \) y parámetro de forma derecha\( b = 2 \).
- La distribución exponencial-logarítmica con parámetro de forma\( p = 0.1 \) y parámetro de escala\( b = 1 \).
- La distribución de Gompertz con paraemter de forma\( a = 1 \) y parámetro de escala\( b = 1 \).
- La distribución de Wald con parámetros de media\( \mu = 1 \) y forma\( \lambda = 1 \).
- La distribución de Weibull con parámetro de forma\( k = 2 \) y parámetro de escala\( b = 1 \).


