16.23: Cadenas de ramificación de tiempo continuo
- Page ID
- 151981
Teoría Básica
Introducción
Genéricamente, supongamos que tenemos un sistema de partículas que pueden generar o dividirse en otras partículas del mismo tipo. Aquí hay algunos ejemplos típicos:
- Las partículas son organismos biológicos que se reproducen.
- Las partículas son neutrones en una reacción en cadena.
- Las partículas son electrones en un multiplicador de electrones.
Suponemos que la vida útil de cada partícula se distribuye exponencialmente con parámetro\( \alpha \in (0, \infty) \), y al final de su vida, se sustituye por un número aleatorio de nuevas partículas a las que nos referiremos como hijos de la partícula original. El número de hijos\( N \) de una partícula tiene función de densidad de probabilidad\( f \) en\( \N \). Las partículas actúan de manera independiente, por lo que además de estar distribuidas de manera idéntica, las vidas y el número de hijos son independientes de partícula a partícula. Por último, asumimos eso\( f(1) = 0 \), de manera que una partícula no puede simplemente morir y ser reemplazada por una sola nueva partícula. Dejar\( \mu \) y\( \sigma^2 \) denotar la media y varianza del número de crías de una sola partícula. Entonces\[ \mu = \E(N) = \sum_{n=0}^\infty n f(n), \quad \sigma^2 = \var(N) = \sum_{n=0}^\infty (n - \mu)^2 f(n) \] asumimos que\( \mu \) es finito y así tiene\( \sigma^2 \) sentido. En nuestro estudio de las cadenas de Markov de tiempo discreto, estudiamos las cadenas ramificadas en términos de tiempo generacional. Aquí queremos estudiar el modelo en tiempo real.
Dejar\( X_t \) denotar el número de partículas a la vez\( t \in [0, \infty) \). Entonces\( \bs{X} = \{X_t: t \in [0, \infty)\} \) es una cadena de Markov en tiempo continuo\( \N \), conocida como cadena de ramificación. La función de parámetro exponencial\( \lambda \) y la matriz de transición de salto\( Q \) vienen dadas por
- \( \lambda(x) = \alpha x \)para\( x \in \N \)
- \(Q(x, x + k - 1) = f(k)\)para\( x \in \N_+ \) y\( k \in \N \).
Prueba
Esa\( \bs X \) es una cadena de Markov de tiempo continuo se desprende de los supuestos y la estructura básica de las cadenas de Markov de tiempo continuo. En resulta que la suposición que\( \mu \lt \infty \) implica que\( \bs X \) es regular, de manera que\( \tau_n \to \infty \) como\( n \to \infty \), donde\( \tau_n \) esta el tiempo del\( n \) th salto para\( n \in \N_+ \).
- Comenzando con\( x \) partículas, el tiempo del primer cambio de estado es el mínimo de variables\( x \) independientes, cada una distribuida exponencialmente con parámetro\( \alpha \). Como sabemos, este mínimo también se distribuye exponencialmente con parámetro\( \alpha x \).
- Comenzando en estado\( x \in \N_+ \), el siguiente estado será\( x + k - 1 \) para\( k \in \N \), si la partícula muere y deja a\( k \) los niños en su lugar. Esto sucede con probabilidad\( f(k) \).
Por supuesto 0 es un estado absorbente, ya que este estado significa extinción sin partículas. (Tenga en cuenta que\( \lambda(0) = 0 \) y así por defecto,\( Q(0, 0) = 1 \).) Entonces, con una cadena de ramificación, existen esencialmente dos tipos de comportamiento: la extinción poblacional o la explosión poblacional.
Para la cadena de ramificación ocurre\( \bs X = \{X_t: t \in [0, \infty)\} \) uno de los siguientes eventos con probabilidad 1:
- Extinción:\( X_t = 0 \) para algunos\( t \in [0, \infty) \) y por lo tanto\( X_s = 0 \) para todos\( s \ge t \).
- Explosión:\( X_t \to \infty \) como\( t \to \infty \).
Prueba
Si\( f(0) \gt 0 \) entonces todos los estados conducen al estado absorbente 0 y por lo tanto el conjunto de estatias positivas\( \N_+ \) es transitorio. Con probabilidad 1, la cadena de salto\( \bs Y \) visita un estado transitorio solo finitamente muchas veces, así que con probabilidad 1 ya sea\( Y_n = 0 \) para algunos\( n \in \N \) o\( Y_n \to \infty \) como\( n \to \infty \). Si\( f(0) = 0 \) entonces\( Y_n \) está aumentando estrictamente en\( n \), ya que\( f(1) = 0 \) por suposición. De ahí con probabilidad 1,\( Y_n \to \infty \) como\( n \to \infty \).
Sin la suposición de que\( \mu \lt \infty \), la explosión puede ocurrir realmente en tiempo finito. Por otro lado, la suposición que\( f(1) = 0 \) es por conveniencia. Sin esta suposición,\( \bs X \) seguiría siendo una cadena de Markov en tiempo continuo, pero como se discutió en la Introducción, la función de parámetro exponencial sería\( \lambda(x) = \alpha f(1) x \) para\( x \in \N \) y la matriz de transición de salto sería\[ Q(x, x + k - 1) = \frac{f(k)}{1 - f(1)}, \quad x \in \N_+, \; k \in \{0, 2, 3, \ldots\} \]
Debido a que todas las partículas actúan de manera idéntica e independiente, la cadena de ramificación que comienza con\( x \in \N_+ \) partículas es esencialmente copias\( x \) independientes de la cadena de ramificación comenzando con 1 partícula. En muchos sentidos, esta es la visión fundamental de las cadenas de ramificación, y en particular, significa que a menudo podemos condicionar\( X(0) = 1 \).
Generador y Matrices de Transición
Como es habitual, vamos a dejar\( \bs P = \{P_t: t \in [0, \infty)\} \) denotar el semigrupo de matrices de transición de\( \bs X \),\( P_t(x, y) = \P(X_t = y \mid X = x) \) para que para\( (x, y) \in \N^2 \). De igual manera,\( G \) denota la matriz generadora infinitesimal de\( \bs X \).
El generador infinitesimal\( G \) viene dado por\ begin {align*} G (x, x) & = -\ alpha x,\ quad x\ in\ N\ G (x, x + k - 1) & =\ alpha x f (k),\ quad x\ in\ N_+,\, k\ in\ N\ end {align*}
Prueba
Esto se deduce inmediatamente de la función de parámetro exponencial y la matriz de transición de salto anterior.
La ecuación hacia atrás de Kolmogorov es\[ \frac{d}{dt} P_t(x, y) = -\alpha x P_t(x, x) + \alpha x \sum_{k=0}^\infty f(k) P_t(x + k - 1, y), \quad (x, y) \in \N^2 \]
Prueba
La ecuación hacia atrás es\( \frac{d}{dt} P_t = G P_t \), por lo que el resultado se desprende del teorema anterior.
A diferencia de algunos de nuestros otros modelos de tiempo continuo, la cadena de salto que\( Q \) se\( \bs Y \) rige no es la versión de tiempo discreto del modelo. Es decir, no\( \bs Y \) es una cadena de ramificación discreta en el tiempo, ya que en el tiempo discreto, el índice\( n \) representa la generación\( n \) th, mientras que aquí representa la\( n \) ésima vez que se reproduce una partícula. Sin embargo, hay muchas cadenas de ramificación de tiempo discreto incrustadas en la cadena de tiempo continua.
Fijar\( t \in (0, \infty) \) y definir\( \bs Z_t = \{X_{n t}: n \in \N\} \). Entonces\( \bs Z_t \) es una cadena de ramificación de tiempo discreto con función de densidad de probabilidad de descendencia\( f_t \) dada por\( f_t(x) = P_t(1, x) \) for\( x \in \N \).
Prueba
En general, sabemos que el muestreo de una cadena de Markov de tiempo continuo (homogénea) a múltiplos de un fijo\( t \in (0, \infty) \), da como resultado una cadena de Markov de tiempo discreto (homogénea). \( \bs Z_t \)Para ser una cadena ramificadora, sólo hay que señalar que\[ P_t(x, y) = f_t^{*x}(y), \quad (x, y) \in \N^2 \] dónde\( f_t^{*x} \) está el poder de convolución\( f_t \) de orden\( x \). Esto es consecuencia del hecho fundamental de que\( X_t \) dado\( X_0 = x \) tiene la misma distribución que la suma de copias\( x \) independientes de\( X_t \) dado\( X_0 = 1 \). Recordemos que el PDF de una suma de variables independientes es la convolución de los PDFs individuales.
Funciones Generadoras de Probabilidad
Como en el caso discreto, las funciones de generación de probabilidad son una herramienta analítica importante para las cadenas de ramificación de tiempo continuo.
Para\( t \in [0, \infty) \) let\( \Phi_t \) denotar la función generadora de probabilidad de\( X_t \) dado\( X_0 = 1 \)\[ \Phi_t(r) = \E\left(r^{X_t} \mid X_0 = 1\right) = \sum_{x=0}^\infty r^x P_t(1, x) \] Let\( \Psi \) denotar la función generadora de\( N \)\[\Psi(r) = \E\left(r^N\right) = \sum_{n=0}^\infty r^n f(n)\] probabilidad de Las funciones generadoras se definen (las series son absolutamente convergentes) al menos para\( r \in (-1, 1] \).
La colección de funciones generadoras\( \bs \Phi = \{\Phi_t: t \in [0, \infty)\} \) da la misma información que la colección de funciones de densidad de probabilidad\( \{P_t(1, \cdot): t \in [0, \infty)\} \). Con la visión fundamental de que el proceso de ramificación a partir de una partícula determina el proceso de ramificación en general, en\( \bs \Phi \) realidad determina el semigrupo de transición\( \bs P = \{P_t: t \in [0, \infty)\} \).
Para\( t \in [0, \infty) \) y\( x \in \N \), la función generadora de probabilidad de\( X_t \) dado\( X_0 = x \) es\( \Phi_t^x \):\[ \sum_{y=0}^\infty r^y P_t(x, y) = [\Phi_t(r)]^x \]
Prueba
Nuevamente, dado\( X_0 = x \), el número de partículas\( X_t \) a la vez\( t \) tiene la misma distribución que la suma de copias\( x \) independientes de\( X_t \) dado\( X_0 = 1 \). Recordemos que el PGF de una suma de variables independientes es el producto de las PGF de las variables.
Tenga en cuenta que\( \Phi_t \) es la función generadora de la distribución de descendencia para la cadena de ramificación de tiempo discreto incrustada\( \bs Z_t = \{X_{n t}: n \in \N\} \) para\( t \in (0, \infty) \). Por otro lado,\( \Psi \) es la función generadora de la distribución de descendencia para la cadena de tiempo continua. Entonces nuestro principal objetivo en esta discusión es ver cómo\( \bs{\Phi} \) se construye a partir de\( \Psi \). Porque\( \bs P \) es un semigrupo bajo multiplicación matricial, y porque las partículas actúan de manera idéntica e independiente,\( \bs \Phi \) es un semigrupo bajo composición.
\( \Phi_{s+t} = \Phi_s \circ \Phi_t \)para\( s, \, t \in [0, \infty) \).
Prueba
Usando la propiedad semigrupo (las ecuaciones Chapman-Kolmogorov) y el resultado anterior tenemos\ begin {align*}\ Phi_ {s+t} (r) & =\ sum_ {y=0} ^\ infty r^y P_ {s+t} (1, y) =\ sum_ {y=0} ^\ infty r^y\ sum_ {x=0} ^ infty r^y\ sum_ {x=0} ^ infty r^y\ sum_ {x=0} ^ infty P_s (1, x) P_t (x, y) =\ suma_ {x=0} ^\ infty P_s (1, x)\ sum_ {y=0} ^\ infty r^y P_t (x, y)\\ & =\ sum_ {x=0} ^\ infty P_s (1, x) [\ phi_t (r)] ^x =\ phi_s [\ phi_t (r)]\ end {align*}
Tenga en cuenta también que\( \Phi_0(r) = \E(r^{X_0} \mid X_0 = 1) = r \) para todos\( r \in \R \). Esto también se desprende de la propiedad semigrupo:\( \Phi_0 = \Phi_0 \circ \Phi_0 \). La relación fundamental entre la colección de funciones generadoras\( \bs \Phi \) y la función generadora\( \Psi \) se da en el siguiente teorema:
El mapeo\( t \mapsto \Phi_t \) satisface la ecuación diferencial\[ \frac{d}{dt} \Phi_t = \alpha (\Psi \circ \Phi_t - \Phi_t) \]
Prueba
Usando la ecuación hacia atrás de Kolmogorov tenemos\[ \frac{d}{dt} \Phi_t(r) = \sum_{x=0}^\infty r^x \frac{d}{dt} P_t(1, x) = \sum_{x=0}^\infty r^x G P_t(1, x) \] Usando el generador anterior,\[ G P_t(1, x) = \sum_{y = 0}^\infty G(1, y) P_t(y, x) = - \alpha P_t(1, x) + \sum_{k=0}^\infty \alpha f(k) P_t(k, x), \quad x \in \N \] Sustituyendo y usando el resultado anterior da\ begin {align*}\ frac {d} {dt}\ phi_t (r) & =\ sum_ {x=0} ^\ infty r^x\ left [-\ alpha p_t (1, x) +\ sum_ {k=0} ^\ infty\ alpha f () P_t (k, x)\ derecha] = -\ alfa\ suma_ {x=0} ^\ infty r^x P_t (1, x) +\ alfa\ suma_ {x=0} ^\ infty\ suma_ {k=0} ^\ infty r^x f (k) p_t (k, x)\\ & = -\ alfa\ phi_t (r) +\ alfa\ sum_ {k=0}\ infty f (k)\ sum_ {x=0} ^\ infty r^x P_t (k, x) = -\ alfa\ psi_t (r) +\ alfa\ suma_ {k=0} ^\ infty f (k) [\ phi_t (r)] ^k = -\ alfa\ phi_t (r) +\ alpha\ Psi [\ phi_t ()]\ end { alinear*}
Esta ecuación diferencial, junto con la condición inicial\( \Phi_0(r) = r \) para todos,\( r \in \R \) determina la colección de funciones generadoras\( \bs \Phi \). De hecho, una solución implícita para\( \Phi_t(r) \) viene dada por la ecuación integral\[ \int_r^{\Phi_t(r)} \frac{1}{\Psi(u) - u} du = \alpha t \] Otra relación se da en el siguiente teorema. Aquí,\( \Phi_t^\prime \) se refiere a la derivada de la función generadora\( \Phi_t \) con respecto a su argumento, por supuesto (so\( r \), no\( t \)).
Para\( t \in [0, \infty) \),\[ \Phi_t^\prime = \frac{\Psi \circ \Phi_t - \Phi_t}{\Psi - \Phi_0} \]
Prueba
De la propiedad semigrupo, tenemos\( \Phi_{t+s}(r) = \Phi_t[\Phi_s(r)] \) para\( s, \, t \in [0, \infty) \). Diferenciar con respecto\( s \) y usar la regla de la cadena junto con el teorema anterior da\[ \frac{d}{ds} \Phi_{t+s}(r) = \Phi_t^\prime[\Phi_s(r)] \frac{d}{ds} \Phi_s(r) = \Phi_t^\prime[\Phi_s(r)] \alpha \left[ \Psi(\Phi_s(r)) - \Phi_s(r)\right] \] Evaluando en\( s = 0 \) y usando la condición que\( \Phi_0(r) = r \) tenemos\[ \frac{d}{dt}\Phi_t(r) = \Phi_t^\prime(r) \alpha [\Psi(r) - r] \] Usando el teorema anterior una vez más da\[ \alpha \left[\Psi(\Phi_t(r)) - \Phi_t(r)\right] = \Phi_t^\prime(r) \alpha[\Psi(r) - r] \] Resolviendo para\( \Phi_t^\prime(r) \) da el resultado.
Momentos
En esta discusión, estudiaremos la media y varianza del número de partículas a la vez\( t \in [0, \infty) \). Dejar\[ m_t = \E(X_t \mid X_0 = 1), \; v_t = \var(X_t \mid X_0 = 1), \quad t \in [0, \infty) \] así que eso\( m_t \) y\( v_t \) son la media y varianza, comenzando con una sola partícula. Como siempre con un proceso de ramificación, basta con considerar una sola partícula:
Para\( t \in [0, \infty) \) y\( x \in \N \),
- \( \E(X_t \mid X_0 = x) = x \, m_t \)
- \( \var(X_t \mid X_0 = x) = x \, v_t \)
Prueba
Una vez más, la distribución de\( X_t \) dado\( X_0 = x \) es la misma que la distribución de la suma de copias\( x \) independientes de\( X_t \) dado\( X_0 = 1 \). Recordemos que la media de una suma de variables es la suma de las medias individuales, y la varianza de la suma de variables independientes es la suma de las varianzas individuales.
Recordemos también que\( \mu \) y\( \sigma^2 \) son la media y varianza del número de crías de una partícula. Aquí está la conexión entre los medios:
\( m_t = e^{\alpha(\mu - 1) t} \)para\( t \in [0, \infty) \).
- Si\( \mu \lt 1 \) entonces\( m_t \to 0 \) como\( t \to \infty \). Esto es extinción en la media.
- Si\( \mu \gt 1 \) entonces\( m_t \to \infty \) como\( t \to \infty \). Esto es explosión en la media.
- Si\( \mu = 1 \) entonces\( m_t = 1 \) para todos\( t \in [0, \infty) \). Esto es estabilidad en la media.
Prueba
A partir de la prueba del teorema anterior,\[ \frac{d}{dt} \Phi_t(r) = \alpha \Phi_t^\prime(r) [\Psi(r) - r] \] Diferenciando con respecto a\( r \), intercambiando el orden de integración a la izquierda, y usando la regla del producto a la derecha da\[ \frac{d}{dt} \Phi_t^\prime(r) = \alpha \Phi_t^{\prime \prime}(r)[\Psi(r) - r] + \alpha \Phi_t^\prime(r)[\Psi^\prime(r) - 1] \] Ahora vamos\( r = 1 \) y recordemos eso\( \Phi(1) = 1 \). Obtenemos\[ \frac{d}{dt} \Phi_t^\prime(1) = \alpha \Phi_t^\prime(1)[\Psi^\prime(1) - 1] \] De la teoría básica de la probabilidad generando funciones,\( m_t = \Phi_t^\prime(1) \) y de manera similar,\( \mu = \Psi^\prime(1) \). De ahí que tengamos Por\[ \frac{d}{dt} m_t = \alpha (\mu - 1) m_t \] supuesto que tenemos la condición inicial\( m_0 = 1 \).
Este resultado es intuitivamente muy atractivo. En función del tiempo, el número esperado de partículas crece o se desintegra exponencialmente, dependiendo de si el número esperado de descendencia de una partícula es mayor o menor que uno. La conexión entre las varianzas es más complicada. Eso lo asumimos\( \sigma^2 \lt \infty \).
Si\( \mu \ne 1 \) entonces\[ v_t = \left[\frac{\sigma^2}{\mu - 1} + (\mu - 1)\right]\left[e^{2 \alpha (\mu - 1) t} - e^{\alpha (\mu - 1) t}\right], \quad t \in [0, \infty) \] Si\( \mu = 1 \) entonces\( v_t = \alpha \sigma^2 t \).
- Si\( \mu \lt 1 \) entonces\( v_t \to 0 \) como\( t \to \infty \)
- Si\( \mu \ge 1 \) entonces\( v_t \to \infty \) como\( t \to \infty \)
Prueba
Las funciones generadoras de probabilidad están naturalmente conectadas a los momentos factoriales, por lo que es mejor trabajar con estos. Por lo tanto, vamos\( w_t = \E[X_t(X_t - 1) \mid X_0 = 1]\)\( t \in [0, \infty) \) y vamos\( \delta = \E[N(N - 1)] \). Estos son los momentos factoriales del orden 2. En la prueba del último teorema demostramos que\[ \frac{d}{dt} \Phi_t^\prime(r) = \alpha \Phi_t^{\prime \prime}(r)[\Psi(r) - r] + \alpha \Phi_t^\prime(r)[\Psi^\prime(r) - 1] \] Diferenciar con respecto a\( r \) nuevamente da\[ \frac{d}{dt} \Phi_t^{\prime \prime}(r) = \alpha \Phi_t^{\prime \prime \prime}(r)[\Psi(r) - r] + 2 \alpha \Phi_t^{\prime \prime}(r)[\Psi^\prime(r) - 1] + \alpha \Phi_t^\prime(r) \Psi^{\prime \prime}(r) \] Ahora sustituto\( r = 1 \). Recordemos que\( \Phi_t^{\prime \prime}(1) = w_t \)\( \Phi_t^\prime(1) = m_t = e^{\alpha (\mu - 1) t} \),,\( \Psi^{\prime \prime}(1) = \delta \),\( \Psi^\prime(1) = \mu \), y\( \Psi(1) = 1 \). Obtenemos la ecuación diferencial\[ \frac{d}{dt} w_t = 2 \alpha (\mu - 1) w_t + \alpha \delta e^{\alpha (\mu - 1) t} \] con la condición inicial\( w_0 = 0 \).
Supongamos que\( \mu \ne 1 \). Luego usando métodos estándar para una lineal, ecuaciones diferenciales de primer orden con coeficientes constantes y una función de forzamiento exponencial, la solución es\[ w_t = \frac{\delta}{\mu - 1}\left[e^{2 \alpha (\mu - 1)} - e^{\alpha (\mu - 1) t}\right] \] Pero\( \delta = \sigma^2 + \mu^2 - \mu \), y de manera similar\( w_t = v_t + m_t^2 - m_t \) con\( m_t = e^{\alpha (\mu - 1) t} \). Sustitución y algo de álgebra luego da el resultado.
Supongamos ahora eso\( \mu = 1 \). Entonces también\( m_t = 1 \) para todos\( t \in [0, \infty) \) y así\( \delta = \sigma^2 \) y\( v_t = w_t \). La ecuación diferencial anterior se reduce simplemente a\[ \frac{d}{dt} v_t = \alpha \sigma^2 \] con condición inicial\( v_0 = 0 \) tan trivialmente\( v_t = \alpha \sigma^2 t \). Por último, en el contexto de la parte b), señalar que si\( \mu = 1 \) debemos tener\( \sigma^2 \gt 0 \) desde entonces lo hemos asumido\( f(1) = 0 \).
Si es\( \mu \lt 1 \) así que\( m_t \to 0 \) como\( t \to \infty \) y tenemos extinción en la media, entonces\( v_t \to 0 \) como\( t \to \infty \) también. Si es\( \mu \gt 1 \) así que\( m_t \to \infty \) como\( t \to \infty \) y tenemos explosión en la media, entonces\( v_t \to \infty \) como\( t \to \infty \) también. Nosotros esperaríamos estos resultados. Por otro lado, si es\( \mu = 1 \) así que\( m_t = 1 \) para todos\( t \in [0, \infty) \) y tenemos estabilidad en la media, entonces\( v_t \) crece linealmente en\( t \). Esto da una idea de qué esperar a continuación cuando consideramos la probabilidad de extinción.
La probabilidad de extinción
Como se muestra anteriormente, existen dos tipos de comportamiento para un proceso de ramificación, ya sea la extinción poblacional o la explosión poblacional. En esta discusión, estudiamos la probabilidad de extinción, comenzando como de costumbre con una sola partícula: ¿\[ q = \P(X_t = 0 \text{ for some } t \in (0, \infty) \mid X_0 = 1) = \lim_{t \to \infty} \P(X_t = 0 \mid X_0 = 1) \]Necesitamos decirlo? La probabilidad de extinción comenzando con un número arbitrario de partículas es fácil.
Para\( x \in \N \),\[ \P(X_t = 0 \text{ for some } t \in (0, \infty) \mid X_0 = x) = \lim_{t \to \infty} \P(X_t = 0 \mid X_0 = x) = q^x \]
Prueba
Dado\( X_0 = x \), la extinción ha ocurrido por el tiempo\( t \) si y sólo si la extinción ha ocurrido por el tiempo\( t \) para cada una de las cadenas ramificadas\( x \) independientes formadas a partir de los descendientes de las partículas\( x \) iniciales.
Podemos relacionar fácilmente la extinción de la cadena de ramificación de tiempo continuo\( \bs X \) con la extinción de cualquiera de las cadenas de ramificación de tiempo discreto incrustadas.
Si la extinción ocurre para\( \bs X \) entonces la extinción ocurre\( \bs Z_t \) para cada uno\( t \in (0, \infty) \). Por el contrario, si la extinción ocurre\( \bs Z_t \) para algunos\( t \in (0, \infty) \) entonces la extinción ocurre\( \bs Z_t \) para cada uno\( t \in (0, \infty) \) y la extinción ocurre para\( \bs X \). De ahí\( q \) es la solución mínima en\( (0, 1] \) de la ecuación\(\Phi_t(r) = r\) para cada\( t \in (0, \infty) \).
Prueba
Las declaraciones sobre el suceso de extinción se derivan inmediatamente del hecho de que\( 0 \) está absorbiendo, de modo que si\( X_t = 0 \) para algunos\( t \in (0, \infty) \) entonces\( X_s = 0 \) para cada uno\( s \in [t, \infty) \). El resultado para la probabilidad de extinción\( q \) se desprende de la teoría de las cadenas de ramificación discreta en el tiempo.
Entonces, si la extinción es cierta o no depende del parámetro crítico\( \mu \).
La probabilidad de extinción\( q \) y la media de la distribución de la descendencia\( \mu \) se relacionan de la siguiente manera:
- Si\( \mu \le 1 \) entonces\( q = 1 \), entonces la extinción es cierta.
- Si\( \mu \gt 1 \) entonces\( 0 \lt q \lt 1 \), entonces hay una probabilidad positiva de extinción y una probabilidad positiva de explosión.
Prueba
Estos resultados se derivan de los resultados correspondientes para cadenas de ramificación de tiempo discreto. Fijar\( t \in (0, \infty) \) y recordar que\( m_t \) es la media de la distribución de descendencia para la cadena discreta de tiempo\( \bs Z_t = \{X_{nt}: n \in \N\} \). Del resultado anterior,
- Si\( \mu \le 1 \) entonces\( m_t \le 1 \).
- Si\( \mu \gt 1 \) entonces\( m_t \gt 1 \).
Sería bueno tener una ecuación para\( q \) en términos de la función generadora de probabilidad de descendencia\( \Psi \). Esto también es fácil
La probabilidad de extinción\( q \) es la solución mínima en\( (0, 1] \) la ecuación\( \Psi(r) = r \).
Prueba
Del resultado anterior,\( \Phi_t(q) = 1 \) para cada\( t \in (0, \infty) \). Sustituyendo\( r = q \) en la ecuación diferencial anterior, tenemos\( \frac{d}{dt} \Phi_t(q) = 0 \) y por lo tanto\( \Psi(q) = q \). Al igual que en la teoría de las cadenas de ramificación discretas, la ecuación solo\( \Psi(r) = r \) tiene la solución 1 en (0, 1] si\( \mu = \Psi^\prime(1) \le 1 \) o hay dos soluciones\( q \in (0, 1) \) y\( 1 \) si\( \mu \gt 0 \). En ambos casos,\( q \) es la solución más pequeña.
Modelos Especiales
Ahora dirigimos nuestra atención a una serie de cadenas de ramificación especiales que son importantes en las aplicaciones o conducen a ideas interesantes. Utilizaremos la notación establecida anteriormente, de manera que ese\( \alpha \) es el parámetro de la vida exponencial de una partícula,\( Q \) es la matriz de transición de la cadena de salto,\( G \) es la matriz generadora infinitesimal, y\( P_t \) es la matriz de transición en el momento\( t \in [0, \infty) \). De igual manera\( m_t = \E(X_t \mid X_0 = x) \)\( v_t = \var(X_t \mid X_0 = x) \),, y\( \Phi_t \) son la media, varianza, y función generadora del número de partículas en el tiempo\( t \in [0, \infty) \), comenzando con una sola partícula. Como siempre, asegúrate de probar estos ejercicios tú mismo antes de mirar las pruebas y soluciones.
La cadena de ramificación de la muerte pura
Primero consideramos la cadena de ramificación en la que cada partícula simplemente muere sin descendencia. Tristemente para estas partículas, la extinción es inevitable, pero este caso sigue siendo un buen lugar para comenzar porque el análisis es sencillo y lleva a fórmulas explícitas. Así, supongamos que\( \bs X = \{X_t: t \in [0, \infty)\} \) es un proceso de ramificación con parámetro de vida útil\( \alpha \in (0, \infty) \) y función de densidad de probabilidad de descendencia\( f \) con\( f(0) = 1 \).
La matriz de transición de la cadena de salto y la matriz generadora están dadas por
- \( Q(0, 0) = 1 \)y\( Q(x, x - 1) = 1 \) para\( x \in \N_+ \)
- \( G(x, x) = - \alpha x \)para\( x \in \N \) y\( G(x, x - 1) = \alpha x \) para\( x \in \N_+ \)
Las funciones variables en el tiempo son más interesantes.
Vamos\( t \in [0, \infty) \). Entonces
- \( m_t = e^{-\alpha t} \)
- \( v_t = e^{-\alpha t} - e^{-2 \alpha t} \)
- \( \Phi_t(r) = 1 - (1 - r) e^{-\alpha t} \)para\( r \in \R \)
- Dada\( X_0 = x \) la distribución de\( X_t \) es binomial con parámetro de ensayo\( x \) y parámetro de éxito\( e^{-\alpha t} \). \[ P_t(x, y) = \binom{x}{y} e^{-\alpha t y} (1 - e^{-\alpha t})^{x - y}, \quad x \in \N, \, y \in \{0, 1, \ldots, x\} \]
Prueba Directa
Todos estos resultados se derivan de los métodos generales anteriores, con\( \mu = \sigma = 0 \) y\( \Psi(r) = 1 \) para\( r \in \R \). Pero es útil dar pruebas directas. Dado\( X_0 = 1 \), deja\( \tau \) ser el tiempo hasta la primera transición, que es simplemente la vida útil de la partícula. Así lo\( \tau \) ha hecho la distribución exponencial con parámetro\( \alpha \). Porque\( t \in [0, \infty) \),\( X_t \) es una variable aleatoria indicadora (tomando solo los valores 0 y 1) con la\[ \P(X_t = 1 \mid X_0 = 1) = \P(\tau \gt t \mid X_0 = 1) = e^{-\alpha t} \] Parte (a), (b) y (c) son resultados estándar para una variable indicadora. Para la parte (d), dada\( X_0 = x \), cada una de las\( x \) partículas, independientemente, sigue viva en el momento\( t \) con probabilidad\( e^{-\alpha t} \). De ahí que el número de partículas aún vivas tenga la distribución binomial con parámetros\( x \) y\( e^{-\alpha t} \).
En particular, tenga en cuenta que\( P_t(x, 0) = (1 - e^{-\alpha t})^x \to 1 \) como\( t \to \infty \). es decir, la probabilidad de extinción por el tiempo\( t \) aumenta a 1 exponencialmente rápido. Como tenemos una fórmula explícita para las matrices de transición, también podemos encontrar una fórmula explícita para las matrices potenciales. El resultado utiliza la función beta\( B \).
Para\( \beta \in (0, \infty) \) la matriz potencial\( U_\beta \) viene dada por\[ U_\beta(x, y) = \frac{1}{\alpha} \binom{x}{y} B(y + \beta / \alpha, x - y + 1), \quad x \in \N, \, y \in \{0, 1, \ldots, x\} \] For\( \beta = 0 \), la matriz potencial\( U \) viene dada por
- \( U(x, 0) = \infty \)para\( x \in \N \)
- \( U(x, y) = 1 / \alpha y \)para\( x, \, y \in \N_+ \) y\( x \le y \).
Prueba
Supongamos eso\( \beta \gt 0 \) y aquello\( x, \, y \in \N \) con\( x \le y \). Por definición\[ U_\beta(x, y) = \int_0^\infty e^{-\beta t} P_t(x, y) \, dt = \int_0^\infty e^{-\beta t} \binom{x}{y} e^{-\alpha t y} (1 - e^{-\alpha t})^{x - y} dt\] Sustituir\( u = e^{-\alpha t} \) por lo que\( du = - \alpha e^{-\alpha t} dt \) o equivalentemente\( dt = - du / \alpha u \). Después de algo de álgebra, el resultado es\[ U_\beta(x, y) = \frac{1}{\alpha} \binom{x}{y} \int_0^1 u^{y + \beta / \alpha - 1} (1 - u)^{x - y} du \] Por definición, la última integral es\( B(y + \beta / \alpha, x - y + 1) \).
- Para\( x \in \N \),\[ U(x, 0) = \int_0^\infty (1 - e^{-\alpha t})^x dd = \infty \]
- Para\( x, \, y \in \N_+ \) con\( x \le y \), la derivación anterior y las propiedades de la función beta dan\[ U(x, y) = \frac{1}{\alpha} \binom{x}{y} B(y, x - y + 1) = \frac{1}{\alpha} \binom{x}{y} \frac{(y - 1)! (x - y)!}{x!} = \frac{1}{\alpha y} \]
Podríamos argumentar los resultados para el potencial\( U \) directamente. Recordemos que\( U(x, y) \) es el tiempo esperado pasado en estado\( y \) comenzando en estado\( x \). Ya que 0 es absorbente y todos los estados conducen a 0,\( U(x, 0) = \infty \) para\( x \in \N \). Si\( x, \, y \in \N_+ \) y\( x \le y \), entonces\( x \) lleva a\( y \) con probabilidad 1. Una vez en estado\( y \) el tiempo pasado\( y \) tiene una distribución exponencial con parámetro\( \lambda(y) = \alpha y \), y así lo es la media\( 1 / \alpha y \). Por supuesto, cuando la cadena se va\( y \), nunca regresa.
Recordemos que\( \beta U_\beta \) es una matriz de probabilidad de transición para\( \beta \gt 0 \), y de hecho\( \beta U_\beta(x, \cdot) \) es la función de densidad de probabilidad de\( X_T \) dado\( X_0 = x \) donde\( T \) es independiente de\( \bs X \) tiene la distribución exponencial con parámetro\( \beta \). Para el siguiente resultado, recuerde la notación de potencia ascendente\[a^{[k]} = a ( a + 1) \cdots (a + k - 1), \quad a \in \R, \, k \in \N\]
Para\( \beta \gt 0 \) y\( x \in \N_+ \), la función\( \beta U_\beta(x, \cdot) \) es la función de densidad de probabilidad beta-binomial con parámetros\( x \)\( \beta / \alpha \), y 1. \[ \beta U_\beta(x, y) = \binom{x}{y} \frac{(\beta / \alpha)^{[y]} 1^{[x - y]}}{(1 + \beta / \alpha)^{[x]}}, \quad x \in \N, \, y \in \{0, 1, \ldots x\} \]
Prueba
Del resultado anterior y propiedades de la función beta. \[ \beta U_\beta(x, y) = \frac{\beta}{\alpha} \binom{x}{y} B(y + \beta / \alpha, x - y + 1), \quad x \in \N, \, y \in \{0, 1, \ldots, x\} \]Pero a partir de las propiedades de la función beta,\[B(y + \beta / \alpha, x - y + 1) = B(\beta / \alpha, 1) \frac{(\beta / \alpha)^{[y]} 1^{[x - y]}}{(1 + \beta / \alpha)^{[x]}} = \frac{\alpha}{\beta} \frac{(\beta / \alpha)^{[y]} 1^{[x - y]}}{(1 + \beta / \alpha)^{[x]}}\] Sustitución da el resultado
El Proceso Yule
A continuación consideramos la cadena ramificadora de nacimiento pura en la que cada partícula, al final de su vida útil, es reemplazada por 2 nuevas partículas. Equivalentemente, podemos pensar en partículas que nunca mueren, pero cada partícula da a luz a una nueva partícula a un ritmo constante. Esta cadena podría servir como modelo para una reacción nuclear sin restricciones, y se conoce como el proceso Yule, llamado así por George Yule. Entonces específicamente, dejemos\( \bs X = \{X_t: t \in [0, \infty)\} \) ser la cadena de ramificación con parámetro exponencial\( \alpha \in (0, \infty) \) y función de densidad de probabilidad de descendencia dada por\( f(2) = 1 \). La explosión es inevitable, comenzando con al menos una partícula, pero otras propiedades del proceso de Yule son interesantes. En particular, existen fascinantes paralelismos con la cadena de ramificación de la muerte pura. Dado que 0 es un estado aislado, absorbente, a veces restringiremos nuestra atención a los estados positivos.
La matriz de transición de la cadena de salto y la matriz generadora están dadas por
- \( Q(0, 0) = 1 \)y\( Q(x, x + 1) = 1 \) para\( x \in \N_+ \)
- \( G(x, x) = - \alpha x \)para\( x \in \N \) y\( G(x, x + 1) = \alpha x \) para\( x \in \N_+ \)
Dado que el proceso Yule es un proceso de nacimiento puro y la tasa de natalidad en estado\( x \in \N \) lo es\( \alpha x \), el proceso también se llama la cadena de nacimiento lineal. Al igual que con el proceso de muerte pura, podemos dar la distribución de\( X_t \) específicamente.
Vamos\( t \in [0, \infty) \). Entonces
- \( m_t = e^{\alpha t} \)
- \( v_t = e^{2 \alpha t} - e^{\alpha t} \)
- \( \Phi_t(r) = \frac{r e^{-\alpha t}}{1 - r + r e^{-\alpha t}} \)para\(|r| \lt \frac{1}{1 - e^{-\alpha t}}\)
- Dado\( X_0 = x \),\( X_t \) tiene la distribución binomial negativa encendida\( \N_+ \) con parámetro de parada\( x \) y parámetro de éxito\( e^{-\alpha t} \). \[ P_t(x, y) = \binom{y - 1}{x - 1} e^{-x \alpha t} (1 - e^{-\alpha t})^{y - x}, \quad x \in \N_+, \, y \in \{x, x + 1, \ldots\} \]
Prueba de los resultados generales
Las partes (a) y (b) siguen del momento general resultados anteriores, con\( \mu = 2 \) y\( \sigma^2 = 0 \). Para la parte (c), tenga en cuenta que\( \Psi(r) = r^2 \) para\( r \in \R \), entonces la ecuación integral para\( \Phi_t \) es\[ \int_r^{\Phi_t(r)} \frac{1}{u^2 - u} = \alpha t \] De fracciones parciales\( \frac{1}{u^2 - u} = \frac{1}{u - 1} - \frac{1}{u} \), por lo que el resultado sigue por integración estándar y álgebra. Reconocemos\( \Phi_t \) como la función generadora de probabilidad de la distribución geométrica on\( \N_+ \) with success\( e^{-\alpha t} \), así que para la parte (d) usamos nuestro argumento estándar. Dado\( X_0 = x \in \N_+ \),\( X_t \) tiene la misma distribución que la suma de copias\( x \) independientes de\( X_t \) dado\( X_0 = 1 \), y así esta es la distribución de la suma de variables\( x \) independientes cada una con la distribución geométrica encendida\( \N_+ \) con parámetro\( e^{-\alpha t} \). Pero esta es la distribución binomial negativa en\( \N_+ \) con parámetros\( x \) y\( e^{-\alpha t} \).
Prueba directa
Como es habitual, let\( \tau_0 = 0 \) y let\( \tau_n \) denotar el tiempo de la\( n \) th transición (nacimiento) para\( n \in \N_+ \). Dado\( X_0 = 1 \), la población está\( n \) en el momento\( \tau_{n-1} \). Entonces el intervalo aleatorio\( \tau_n - \tau_{n-1} \) (el tiempo hasta el siguiente nacimiento) tiene la distribución exponencial con parámetro\( \alpha n \) y estos intervalos son independientes como\( n \) varía. De un resultado en la sección sobre la distribución exponencial, se deduce que\( \tau_n = \sum_{k=1}^n (\tau_k - \tau_{k-1}) \) tiene función de distribución dada por\[ \P(\tau_n \le t \mid X_0 = 1) = (1 - e^{-\alpha t})^n, \quad t \in [0, \infty) \] Curiosamente, esta es también la función de distribución del máximo de variables\( n \) independientes, cada una con la distribución exponencial con tasa\( \alpha \). De ahí\[ \P(X_t \ge n \mid X_0 = 1) = \P(\tau_{n - 1} \le t \mid X_0 = 1) = (1 - e^{-\alpha t})^{n - 1}, \quad n \in \N_+ \] y por lo tanto\[ \P(X_t = n \mid X_0 = 1) = \P(X_t \ge n \mid X_0 = 1) - \P(X_t \ge n + 1 \mid X_0 = 1) = (1 - e^{-\alpha t})^{n-1} e^{-\alpha t}, \quad n \in \N_+ \] Así dado\( X_0 = 1 \),\( X_t \) tiene la distribución geométrica con parámetro\( e^{-\alpha t} \). Los otros resultados luego siguen fácilmente.
Recordemos que la distribución binomial negativa con parámetros\( k \in \N_+ \) y\( p \in (0, 1) \) gobierna el número de ensayo del éxito\( k \) th en una secuencia de ensayos de Bernoulli con parámetro de éxito\( p \). Por lo que la ocurrencia de esta distribución en el proceso de Yule sugiere tal interpretación. Sin embargo, esta interpretación no es tan obvia como con la distribución binomial en la cadena de ramificación de la muerte pura. A continuación damos las matrices potenciales.
Para\( \beta \in [0, \infty) \) la matriz\( U_\beta \) potencial viene dada por\[ U_\beta(x, y) = \frac{1}{\alpha} \binom{y - 1}{x - 1} B(x + \beta / \alpha, y - x + 1), \quad x \in \N_+, \, y \in \{x, x + 1, \ldots\} \] If\( \beta \gt 0 \), la función\( \beta U_\beta(x, \cdot) \) es la función de densidad de probabilidad binomial beta negativa con parámetros\( x \)\( \beta / \alpha \), y 1:\[ \beta U_\beta(x, y) = \binom{y - 1}{x - 1} \frac{(\beta / \alpha)^{[x]} 1^{[y - x]}}{(1 + \beta / \alpha)^{[y]}}, \quad x \in \N, \, y \in \{x, x + 1, \ldots\} \]
Prueba
La prueba es muy similar a la anterior. Supongamos eso\( \beta \ge 0 \) y aquello\( x, \, y \in \N_+ \) con\( y \ge x \). Por definición\[ U_\beta(x, y) = \int_0^\infty e^{-\beta t} P_t(x, y) \, dt = \int_0^\infty e^{-\beta t} \binom{y - 1}{x - 1} e^{-\alpha t x} (1 - e^{-\alpha t})^{y - x} dt\] Sustituir\( u = e^{-\alpha t} \) por lo que\( du = - \alpha e^{-\alpha t} dt \) o equivalentemente\( dt = - du / \alpha u \). Después de algo de álgebra, el resultado es\[ U_\beta(x, y) = \frac{1}{\alpha} \binom{y - 1}{x - 1} \int_0^1 u^{x + \beta / \alpha - 1} (1 - u)^{y - x} du \] Por definición, la última integral es\( B(x + \beta / \alpha, y - x + 1) \).
Si pensamos en el proceso de Yule en términos de partículas que nunca mueren, pero cada partícula da a luz a una nueva partícula a ritmo\( \alpha \), entonces podemos estudiar la edad de las partículas en un momento dado. Como es habitual, podemos comenzar con una sola partícula nueva a la hora 0. Entonces, para configurar la notación, dejemos\( \bs X = \{X_t: t \in [0, \infty)\} \) ser la cadena ramificadora de Yule con tasa de natalidad\( \alpha \in (0, \infty) \), y asumamos eso\( X_0 = 1 \). Dejar\( \tau_0 = 0 \) y para\( n \in \N_+ \), dejar\( \tau_n \) denotar el tiempo de la\( n \) th transición (nacimiento).
Para\( t \in [0, \infty) \), vamos a\( A_t \) denotar la edad total de las partículas en el momento\( t \). Entonces\[ A_t = \sum_{n = 0}^{X_t - 1} (t - \tau_n), \quad t \in [0, \infty) \] El proceso aleatorio\( \bs A = \{A_t: t \in [0, \infty)\} \) es el proceso de la edad.
Prueba
Tenga en cuenta que ha habido\( X_t - 1 \) nacimientos en el intervalo\( [0, t] \). Porque\( n \in \{0, 1, \ldots, X_t - 1\} \), la edad en el momento\( t \) de la partícula nacida en el momento\( \tau_n \) es\( t - \tau_n \).
Aquí hay otra expresión para el proceso de la edad.
Nuevamente, deja\( \bs A = \{A_t: t \in [0, \infty)\} \) ser el proceso de edad para la cadena Yule comenzando con una sola partícula. Entonces\[ A_t = \int_0^t X_s ds, \quad t \in [0, \infty) \]
Prueba
Supongamos que\( X_t = k + 1 \) donde\( k \in \N \), así que eso\( \tau_k \le t \lt \tau_{k+1} \). Tenga en cuenta que\( X_s = n \) para\( \tau_{n-1} \le s \lt \tau_n \) y\( n \in \{1, 2, \ldots, k\} \), mientras\( X_s = k + 1 \) para\( \tau_k \le s \le t \). \[ \int_0^t X_s ds = \sum_{n=1}^k n (\tau_n - \tau_{n-1}) + (k + 1) (t - \tau_k) = (k + 1) t - \sum_{n=0}^k \tau_n \]De ahí que del resultado anterior,\[ A_t = \sum_{n=0}^k (t - \tau_n) = (k + 1) t - \sum_{n=0}^k \tau_n \]
Con la última representación, podemos encontrar fácilmente la edad total esperada en el momento\( t \).
Nuevamente, deja\( \bs A = \{A_t: t \in [0, \infty)\} \) ser el proceso de edad para la cadena Yule comenzando con una sola partícula. Entonces\[ \E(A_t) = \frac{e^{\alpha t} - 1}{\alpha}, \quad t \in [0, \infty) \]
Prueba
Podemos intercambiar el valor esperado y la integral por el teorema de Fubini. Entonces, usando el resultado del momento anterior,\[ \E(A_t) = \E\left(\int_0^t X_s ds\right) = \int_0^t \E(X_s) ds = \int_0^t e^{\alpha s} ds = \frac{e^{\alpha t} - 1}{\alpha} \]
La cadena general de ramificación de nacimiento-muerte
A continuación consideramos la cadena de ramificación de tiempo continuo en la que cada partícula, al final de su vida, no deja hijos o dos hijos. En cada transición, el número de partículas aumenta en 1 o disminuye en 1, por lo que dicha cadena de ramificación también es una cadena de nacimiento-muerte en tiempo continuo. Específicamente, dejar\( \bs X = \{X_t: t \in [0, \infty)\} \) ser una cadena de ramificación de tiempo continuo con parámetro de vida útil\( \alpha \in (0, \infty) \) y función de densidad de probabilidad de descendencia\( f \) dada por\( f(0) = 1 - p \),\( f(2) = p \), donde\( p \in [0, 1] \). Cuando\( p = 0 \) tenemos la cadena de muerte pura, y cuando\( p = 1 \) tenemos el proceso de Yule. Ya los hemos estudiado, por lo que el caso interesante es cuando\( p \in (0, 1) \) para que tanto la extinción como la explosión sean posibles.
La matriz de transición de la cadena de salto y la matriz generadora están dadas por
- \(Q(0, 0) = 1\), y\( Q(x, x - 1) = 1 - p \),\( Q(x, x + 1) = p \) para\( x \in \N_+ \)
- \( G(x, x) = -\alpha x \)para\( x \in \N \), y\( G(x, x - 1) = \alpha (1 - p) x \),\( G(x, x + 1) = \alpha p x \) para\( x \in \N_+ \)
Como se mencionó anteriormente, también\( \bs X \) es una cadena de nacimiento-muerte en tiempo continuo\( \N \), con 0 absorbente. En estado\( x \in \N_+ \), la tasa de natalidad es\( \alpha p x \) y la tasa de mortalidad es\( \alpha (1 - p) x \). A continuación se dan las funciones de momento.
Para\( t \in [0, \infty) \),
- \( m_t = e^{\alpha(2 p - 1) t} \)
- Si\( p \ne \frac{1}{2} \),\[ v_t = \left[\frac{4 p (1 - p)}{2 p - 1} + (2 p - 1)\right]\left[e^{2 \alpha (2 p - 1)t} - e^{\alpha (2 p - 1) t}\right] \] Si\( p = \frac{1}{2} \),\( v_t = 4 \alpha p (1 - p) t \).
Prueba
Estos resultados se derivan de las fórmulas generales anteriores para\( m_t \) y\( v_t \), desde\( \mu = 2 p \) y\( \sigma^2 = 4 p (1 - p) \).
El siguiente resultado da la función generadora de la distribución de la descendencia y la probabilidad de extinción.
Para la cadena ramificadora de nacimiento-muerte,
- \(\Psi(r) = p r^2 + (1 - p)\)para\( r \in \R \).
- \( q = 1 \)si\(0 \lt p \le \frac{1}{2} \) y\( q = \frac{1 - p}{p} \) si\( \frac{1}{2} \lt p \lt 1 \).
Prueba
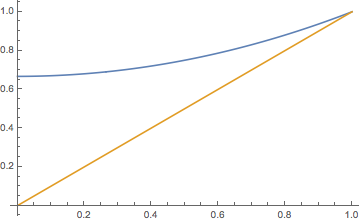
Figura\(\PageIndex{1}\): Gráficas de\( r \mapsto \Psi(r) \) y\( r \mapsto r \) cuándo\( p = \frac{1}{3} \)
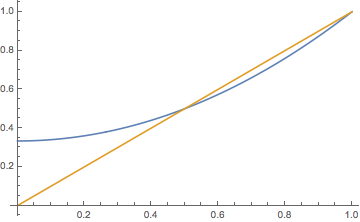
Figura\(\PageIndex{2}\): Gráficas de\( r \mapsto \Psi(r) \) y\( r \mapsto r \) cuándo\( p = \frac{2}{3} \)
Para\( t \in [0, \infty) \), la función generadora\( \Phi_t \) viene dada por\ begin {align*}\ phi_t (r) & =\ frac {p r - (1 - p) + (1 - p) (1 - r) e^ {\ alpha (2 p - 1) t}} {p - (1 - p) + p (1 - r) e^ {\ alpha (2 p - 1) t}},\ quad\ texto {si} p\ ne 1/2\\\ phi_t (r) & =\ frac {2 r + (1 - r)\ alpha t} {2 + (1 - r)\ alpha t},\ quad \ texto {si} p =\ frac {1} {2}\ end {alinear*}
Solución
La ecuación integral para\( \Phi_t \) es\[ \int_r^{\Phi_t(r)} \frac{du}{p u^2 + (1 - p) - u} = \alpha t \] El denominador en los factores integrales en\( (u - 1)[p u - (1 - p)] \). Si\( p \ne \frac{1}{2} \), use fracciones parciales, integración estándar y algo de álgebra. Si\( p = \frac{1}{2} \) el factoring es\( \frac{1}{2}(u - 1)^2 \) y fracciones parciales no es necesario. Nuevamente, use integración estándar y álgebra.


