8.2: Vectores aleatorios y MATLAB
- Page ID
- 150941
m-procedimientos para un par de variables aleatorias simples
Examinamos, primero, cálculos sobre un par de variables aleatorias simples\(X, Y\) consideradas conjuntamente. Estos son, en efecto, dos componentes de un vector aleatorio\(W = (X, Y)\), que mapea desde el espacio básico\(\Omega\) hasta el plano. La distribución inducida está en el\((t, u)\) plano. Los valores en el eje horizontal (\(t\)-eje) corresponden a los valores de la primera variable aleatoria de coordenadas\(X\) y los valores en el eje vertical (eje u) corresponden a valores de\(Y\). Ampliamos la estrategia computacional utilizada para una sola variable aleatoria.
Primero, revisemos la estrategia de una variable. En este caso, los datos consisten en valores\(t_i\) y probabilidades correspondientes dispuestos en matrices
\(X = [t_1, t_2, \cdot\cdot\cdot, t_n]\)y\(PX = [P(X = t_1), P(X = t_2), \cdot\cdot\cdot, P(X = t_n)]\)
Para realizar cálculos\(Z = g(X)\), utilizamos operaciones de matriz\(X\) para formar una matriz
\(G = [g(t_1) g(t_2) \cdot\cdot\cdot g(t_n)]\)
que tiene\(g(t_i)\) en una posición correspondiente a\(P(X = t_i)\) en matriz\(PX\).
Problema básico. Determinar\(P(g(X) \in M)\), dónde\(M\) está algún conjunto prescrito de valores.
- Utilice operaciones relacionales para determinar las posiciones para las cuales\(g(t_i) \in M\). Estos estarán en una matriz cero-uno\(N\), con unos en las posiciones deseadas.
- Seleccione el\(P(X = t_i)\) en las posiciones correspondientes y suma. Esto se logra mediante una de las operaciones de MATLAB para determinar el producto interno de\(N\) y\(PX\)
Extendemos estas técnicas y estrategias a un par de variables aleatorias simples, consideradas conjuntamente.
Los datos para un par\(\{X, Y\}\) de variables aleatorias son los valores de\(X\) y\(Y\), que podemos poner en matrices de fila
y las probabilidades conjuntas\(P(X = t_i, Y = u_j)\) en una matriz\(P\). Por lo general, representamos la distribución gráficamente poniendo la masa de probabilidad\(P(X = t_i, Y = u_j)\)\((t_i, u_j)\) en el punto del plano. Esta probabilidad conjunta puede está representada por la matriz\(P\) con elementos dispuestos correspondientes a los puntos de masa en el plano. Así
Para realizar cálculos, formamos matrices computacionales\(t\) y de\(u\) tal manera que —\(t\) tiene elemento\(t_i\) en cada\((t_i, u_j)\) posición (es decir, en cada punto de la columna\(i\) th de la izquierda) —\(u\) tiene elemento\(u_j\) en cada\((t_i, u_j)\) posición (es decir, en cada punto en la fila\(j\) th desde la parte inferior) MATLAB array y operaciones lógicas on\(t, u, P\) realizar las operaciones especificadas en\(t_i, u_j\), y\(P(X = t_i, Y = u_j)\) en cada\((t_i, u_j)\) posición, de una manera análoga a las operaciones en el caso de una sola variable.
La formación de las matrices t y u se logra mediante un procedimiento básico de configuración m llamado jcalc. Los datos para este procedimiento están en tres matrices:\(X = [t_1, t_2, \cdot\cdot\cdot, t_n]\) es el conjunto de valores para la variable aleatoria\(X\)\(Y = [u_1, u_2, \cdot\cdot\cdot, u_m]\) es el conjunto de valores para la variable aleatoria\(Y\), y\(P = [p_{ij}]\), donde\(p_{ij} = P(X = t_i, Y = u_j)\). Organizamos las probabilidades conjuntas como en el plano, con\(X\) -valores aumentando a la derecha e Y -valores aumentando hacia arriba. Esto es diferente al arreglo habitual en una matriz, en la que los valores de la segunda variable aumentan a la baja. El procedimiento m se encarga de esta inversión. El procedimiento m forma las matrices\(t\) y\(u\), utilizando la función de MATLAB meshgrid, y computa las distribuciones marginales para\(X\) y\(Y\). En el siguiente ejemplo, mostramos los distintos pasos utilizados en el procedimiento de configuración. Ordinariamente, estos pasos intermedios no se mostrarían.
Ejemplo 8.2.7: Configuración y cálculos básicos
>> jdemo4 % Call for data in file jdemo4.m
>> jcalc % Call for setup procedure
Enter JOINT PROBABILITIES (as on the plane) P
Enter row matrix of VALUES of X X
Enter row matrix of VALUES of Y Y
Use array operations on matrices X, Y, PX, PY, t, u, and P
>> disp(P) % Optional call for display of P
0.0360 0.0198 0.0297 0.0209 0.0180
0.0372 0.0558 0.0837 0.0589 0.0744
0.0516 0.0774 0.1161 0.0817 0.1032
0.0264 0.0270 0.0405 0.0285 0.0132
>> PX % Optional call for display of PX
PX = 0.1512 0.1800 0.2700 0.1900 0.2088
>> PY % Optional call for display of PY
PY = 0.1356 0.4300 0.3100 0.1244
- - - - - - - - - - % Steps performed by jcalc
>> PX = sum(P) % Calculation of PX as performed by jcalc
PX = 0.1512 0.1800 0.2700 0.1900 0.2088
>> PY = fliplr(sum(P')) % Calculation of PY (note reversal)
PY = 0.1356 0.4300 0.3100 0.1244
>> [t,u] = meshgrid(X,fliplr(Y)); % Formation of t, u matrices (note reversal)
>> disp(t) % Display of calculating matrix t
-3 0 1 3 5 % A row of X-values for each value of Y
-3 0 1 3 5
-3 0 1 3 5
-3 0 1 3 5
>> disp(u) % Display of calculating matrix u
2 2 2 2 2 % A column of Y-values (increasing
1 1 1 1 1 % upward) for each value of X
0 0 0 0 0
-2 -2 -2 -2 -2
Supongamos que deseamos determinar la probabilidad\(P(X^2 - 3Y \ge 1)\). Usando operaciones de matriz en\(t\) y\(u\), obtenemos la matriz\(G = [g(t_i, u_j)]\).
>> G = t.^2 - 3*u % Formation of G = [g(t_i,u_j)] matrix
G = 3 -6 -5 3 19
6 -3 -2 6 22
9 0 1 9 25
15 6 7 15 31
>> M = G >= 1 % Positions where G >= 1
M = 1 0 0 1 1
1 0 0 1 1
1 0 1 1 1
1 1 1 1 1
>> pM = M.*P % Selection of probabilities
pM =
0.0360 0 0 0.0209 0.0180
0.0372 0 0 0.0589 0.0744
0.0516 0 0.1161 0.0817 0.1032
0.0264 0.0270 0.0405 0.0285 0.0132
>> PM = total(pM) % Total of selected probabilities
PM = 0.7336 % P(g(X,Y) >= 1)
En el Ejemplo 8.1.3 de “Vectores aleatorios y distribuciones conjuntas” observamos que la función de distribución conjunta\(F_{XY}\) es constante sobre cualquier celda de la cuadrícula, incluyendo los límites izquierdo e inferior, en el valor tomado en la esquina inferior izquierda de la celda. Estos valores de esquina inferior izquierda pueden obtenerse sistemáticamente a partir de la matriz de probabilidad conjunta P mediante una operación de dos pasos.
- Tomar sumas acumuladas al alza de las columnas de\(P\).
- Tomar sumas acumuladas de las filas de la matriz resultante.
Esto se puede hacer con la función cumsum de MATLAB, que toma las sumas acumulativas de columnas hacia abajo. Al voltear la matriz y transponer, podemos lograr los resultados deseados.
Ejemplo 8.2.8: Cálculo de los valores F XY para el Ejemplo 8.3 a partir de “Vectores Aleatorios y Distribuciones Conjuntas”
>> P = 0.1*[3 0 0; 0 6 0; 0 0 1];
>> FXY = flipud(cumsum(flipud(P))) % Cumulative column sums upward
FXY =
0.3000 0.6000 0.1000
0 0.6000 0.1000
0 0 0.1000
>> FXY = cumsum(FXY')' % Cumulative row sums
FXY =
0.3000 0.9000 1.0000
0 0.6000 0.7000
0 0 0.1000
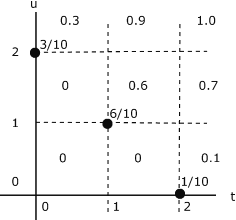
La comparación con el Ejemplo 8.3 de “Vectores Aleatorios y Distribuciones Conjuntas” muestra concordancia con los valores obtenidos a mano.
El procedimiento de dos pasos se ha incorporado en un procedimiento m jddbn. Como ejemplo, volver a la distribución en Ejemplo Ejemplo 8.7
Ejemplo 8.2.9: Función de distribución conjunta por ejemplo 8.7
>> jddbn
Enter joint probability matrix (as on the plane) P
To view joint distribution function, call for FXY
>> disp(FXY)
0.1512 0.3312 0.6012 0.7912 1.0000
0.1152 0.2754 0.5157 0.6848 0.8756
0.0780 0.1824 0.3390 0.4492 0.5656
0.0264 0.0534 0.0939 0.1224 0.1356
Estos valores se pueden poner en una cuadrícula, de la misma manera que en la Figura 8.1.2 para el Ejemplo 8.1.3 en “Vectores Aleatorios y Distribuciones Conjuntas”.
Como en el caso de canónico para una sola variable aleatoria, a menudo es útil tener una versión funcional del procedimiento jcalc para proporcionar la libertad de nombrar convenientemente las salidas. function [x, y, t, u, px, py, p] = jcalcf (X, Y, P) Las cantidades\(x, y, t, u, px, py\), y se les\(p\) puede dar cualquier nombre deseado.
Variables aleatorias absolutamente continuas conjuntas
En el caso de una sola variable, la condición de que no haya concentraciones de masa puntual en la línea asegura la existencia de una función de densidad de probabilidad, útil en los cálculos de probabilidad. Una situación similar existe para una distribución conjunta para dos (o más) variables. Para cualquier mapeo conjunto al plano que asigne probabilidad cero a cada conjunto con área cero (puntos discretos, segmentos de línea o curva, y uniones contables de estos) hay una función de densidad.
Definición
Si la distribución de probabilidad conjunta para el par\(\{X, Y\}\) asigna probabilidad cero a cada conjunto de puntos con área cero, entonces existe una función de densidad conjunta\(f_{XY}\) con la propiedad
\(P[(X, Y) \in Q] = \int \int_{Q} f_{XY}\)
Tenemos tres propiedades análogas a las del caso de una sola variable:
(f1)\(f_{XY} \ge 0\) (f2)\(\int \int_{R^2} f_{XY} = 1\) (f3)\(F_{XY} (t,u) = \int_{-\infty}^{1} \int_{-\infty}^{u} f_{XY}\)
En cada punto de continuidad para\(f_{XY}\), la densidad es el segundo parcial
\(f_{XY} (t, u) = \dfrac{\partial^2 F_{XY} (t, u)}{\partial t \partial u}\)
Ahora
\(F_X (t) = F_{XY} (t, \infty) = \int_{-\infty}^{t} \int_{-\infty}^{\infty} f_{XY} (r, s) dsdr\)
Una expresión similar se mantiene para\(F_Y(u)\). El uso del teorema fundamental del cálculo para obtener las derivadas da el resultado
\(f_X(t) = \int_{-\infty}^{\infty} f_{XY}(t, s) ds\)y\(f_Y(u) = \int_{-\infty}^{\infty} f_{XY} (r, u) du\)
Densidades marginales. Así, para obtener la densidad marginal para la primera variable, integrar la segunda variable en la densidad conjunta, y de manera similar para la marginal para la segunda variable.
Ejemplo 8.2.10: Funciones de densidad marginal
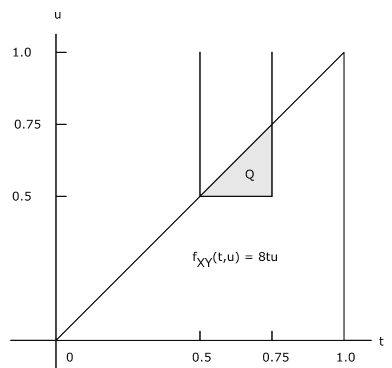
Vamos\(f_{XY} (t, u) = 8tu\)\(0 \le u \le t \le 1\). Esta región es el triángulo delimitado por\(u = 0, u = t\), y\(t = 1\) (ver Figura 8.2.8)
\(f_X(t) = \int f_{XY} (t, u) du = 8t \int_{0}^{1} u du = 4t^3\),\(0 \le t \le 1\)
\(f_Y(u) = \int f_{XY} (t, u) dt = 8u \int_{u}^{1} t dt = 4u(1 - u^2)\),\(0 \le u \le 1\)
\(P(0.5 \le X \le 0.75, Y > 0.5) = P[(X, Y) \in Q]\)donde\(Q\) está la parte común del triángulo con la franja entre\(t = 0.5\) y\(t = 0.75\) y por encima de la línea\(u = 0.5\). Este es el pequeño triángulo delimitado por\(u = 0.5\),\(u = t\), y\(t = 0.75\). Así
\(p = 8 \int_{1/2}^{3/4} \int_{1/2}^{t} tu du dt = 25/256 \approx 0.0977\)
Ejemplo 8.2.11: Distribución marginal con expresión del compuesto
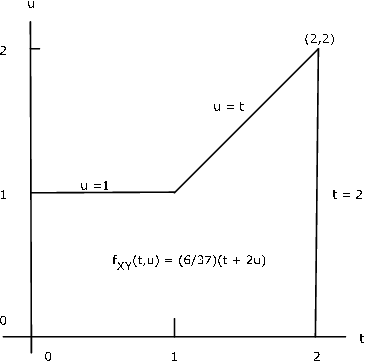
El par\(\{X, Y\}\) tiene densidad de juntas\ f_ {XY} (t, u) =\ dfrac {6} {37} (t + 2u)\) en la región delimitada por\(t = 0, t = 2, u = 0\) y\(u = \text{max} \{1, t\}\) (ver Figura 8.9). Determinar la densidad marginal\(f_X\).
Solución
El examen de la figura muestra que tenemos diferentes límites para la integral con respecto a\(u\) para\(0 \le t \le 1\) y para\(1 < t \le 2\).
- Para\(0 \le t \le 1\)
\(f_x(t) = \dfrac{6}{37} \int_{0}^{1} (t + 2u) du = \dfrac{6}{37} (t + 1)\)
- Para\(1 < t \le 2\)
\(f_X (t) = \dfrac{6}{37} \int_{0}^{1} (t + 2u) du = \dfrac{12}{37} t^2\)
Podemos combinarlos en una sola expresión de una manera ampliamente utilizada en tratamientos posteriores. Supongamos\(M = [0, 1]\) y\(N = (1, 2]\). Luego\(I_M(t) = 1\) para\(t \in M\) (es decir,\(0 \le t \le 1\)) y cero en otra parte. De igual manera,\(I_{N} (t) = 1\) para\(t \in N\) y cero en otros lugares. Podemos, por lo tanto,\(f_X\) expresarnos
Aproximación discreta en el caso continuo
Para un par\(\{X, Y\}\) con densidad de juntas\(f_{XY}\), aproximamos la distribución de una manera similar a la de una sola variable aleatoria. Luego utilizamos las técnicas desarrolladas para un par de variables aleatorias simples. Si tenemos valores\(n\) aproximados\(t_i\) para\(X\) y valores\(m\) aproximados\(u_j\) para\(Y\), entonces tenemos\(n \cdot m\) pares\((t_i, u_j)\), correspondientes a puntos en el plano. Si subdividimos el eje horizontal para valores de\(X\), con incrementos constantes\(dx\), como en el caso de una sola variable, y el eje vertical para valores de\(Y\), con incrementos constantes\(dy\), tenemos una estructura de cuadrícula que consiste en rectángulos de tamaño\(dx \cdot dy\). Seleccionamos\(t_i\) y\(u_j\) en el punto medio de su incremento, de manera que el punto\((t_i, u_j)\) esté en el punto medio del rectángulo. Si dejamos que el par aproximado sea\(\{X^*, Y^*\}\), asignamos
\(p_{ij} = P((X^*, Y^*) = (t_i, u_j)) = P(X^* = t_i, Y^* = u_j) = P((X, Y) \text{ in } ij \text{th rectangle})\)
Como en el caso de una variable, si los incrementos son lo suficientemente pequeños,
\(P((X, Y) \in ij \text{th rectangle}) \approx dx \cdot dy \cdot f_{XY}(t_i, u_j)\)
El procedimiento m tuappr requiere puntos finales de intervalos que incluyen los rangos de\(X\) y\(Y\) y para los números de subintervalos en cada uno. Luego solicita una expresión for\(f_{XY} (t, u)\), a partir de la cual determina la distribución de probabilidad conjunta. Calcula las distribuciones aproximadas marginales y configura las matrices de cálculo\(t\) y al\(u\) igual que el proceso m jcalc para variables aleatorias simples. Luego se realizan cálculos como para cualquier par simple conjunto.
Ejemplo 8.2.12: Aproximación a una distribución continua conjunta
\(f_{XY} (t, u) = 3\)en\(0 \le u \le t^2 \le 1\)
Determinar\(P(X \le 0.8, Y > 0.1)\).
>> tuappr Enter matrix [a b] of X-range endpoints [0 1] Enter matrix [c d] of Y-range endpoints [0 1] Enter number of X approximation points 200 Enter number of Y approximation points 200 Enter expression for joint density 3*(u <= t.^2) Use array operations on X, Y, PX, PY, t, u, and P >> M = (t <= 0.8)&(u > 0.1); >> p = total(M.*P) % Evaluation of the integral with p = 0.3355 % Maple gives 0.3352455531
La aproximación discreta puede ser utilizada para obtener gráficas aproximadas de distribución marginal y funciones de densidad.
Ejemplo 8.2.13: Gráfica aproximada de funciones de densidad marginal y distribución
\(f_{XY} (t, u) = 3u\)en el triángulo delimitado por\(u = 0\),\(u \le 1 + t\), y\(u \le 1 - t\).
>> tuappr
Enter matrix [a b] of X-range endpoints [-1 1]
Enter matrix [c d] of Y-range endpoints [0 1]
Enter number of X approximation points 400
Enter number of Y approximation points 200
Enter expression for joint density 3*u.*(u<=min(1+t,1-t))
Use array operations on X, Y, PX, PY, t, u, and P
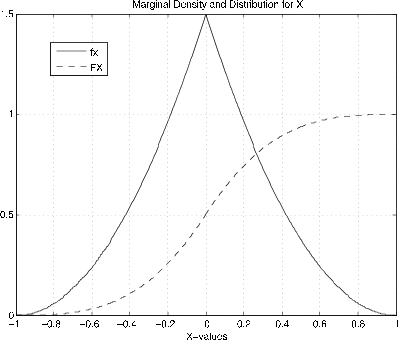
>> fx = PX/dx; % Density for X (see Figure 8.2.10)
% Theoretical (3/2)(1 - |t|)^2
>> fy = PY/dy; % Density for Y
>> FX = cumsum(PX); % Distribution function for X (Figure 8.2.10)
>> FY = cumsum(PY); % Distribution function for Y
>> plot(X,fx,X,FX) % Plotting details omitted
Estas técnicas de aproximación son útiles para tratar funciones de variables aleatorias, expectativas y expectativas condicionales y regresión.


