8.E: Introducción a las pruebas t (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 150822

Foster et al.
University of Missouri-St. Louis, Rice University, & University of Houston, Downtown Campus via University of Missouri’s Affordable and Open Access Educational Resources Initiative

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

¿Cuál es la diferencia entre una\(z\) prueba y una\(t\) prueba de 1 muestra?

Respuesta:: A\(z\) -test utiliza la desviación estándar de la población para calcular el error estándar y obtiene valores críticos basados en la distribución normal estándar. A\(t\) -test utiliza la desviación estándar de la muestra como estimación al calcular el error estándar y obtiene valores críticos de la distribución t en función de los grados de libertad.

¿Qué representa un intervalo de confianza?
¿Cuál es la relación entre un nivel de confianza elegido para un intervalo de confianza y qué tan amplio es ese intervalo? Por ejemplo, si se pasa de un IC del 95% a un IC del 90%, ¿qué sucede? Pista: mira la tabla t para ver cómo cambian los valores críticos cuando cambias los niveles de significación.

Respuesta:: A medida que aumenta el nivel de confianza, el intervalo se hace más amplio. Para hablar con más confianza sobre haber encontrado la media poblacional, es necesario lanzar una red más amplia. Esto sucede porque los valores críticos para mayores niveles de confianza son mayores, lo que crea un margen de error más amplio.

Construir un intervalo de confianza alrededor de la media de la muestra\(\overline{X}\) = 25 para las siguientes condiciones:
1. \(N\)= 25,\(s\) = 15, 95% nivel de confianza
2. \(N\)= 25,\(s\) = 15, 90% nivel de confianza
3. \(s_{\overline{X}}\)= 4.5,\(α\) = 0.05,\(df\) = 20
4. \(s\)= 12,\(df\) = 16 (sí, esa es toda la información que necesitas)
Verdadero o Falso: un intervalo de confianza representa la ubicación más probable de la media de la población verdadera.

Respuesta:: Falso: un intervalo de confianza es un rango de puntuaciones plausibles que pueden o no correlacionar la media real de la población.

Escuchas que los campus universitarios pueden diferir de la población general en términos de afiliación política, y quieres usar pruebas de hipótesis para ver si esto es cierto y, de ser así, qué tan grande es la diferencia. Sabes que la afiliación política promedio en la nación es\(μ\) = 4.00 en una escala de 1.00 a 7.00, por lo que recolectas datos de 150 estudiantes universitarios de todo el país para ver si hay alguna diferencia. Encuentras que el puntaje promedio es de 3.76 con una desviación estándar de 1.52. Use una\(t\) prueba de 1 muestra para ver si hay una diferencia en el nivel\(α\) = 0.05.
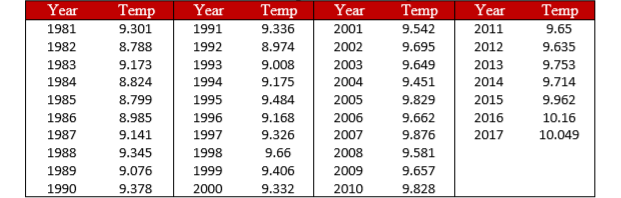
Se oye mucho hablar sobre el aumento de la temperatura global, así que decides ver por ti mismo si ha habido un cambio real en los últimos años. Ya sabes que la temperatura promedio del suelo de 1951-1980 fue de 8.79 grados centígrados. Encuentras datos de temperatura promedio anual de 1981-2017 y decides construir un intervalo de confianza del 99% (porque quieres estar lo más seguro posible y buscar diferencias en ambas direcciones, no solo una) usando estos datos para probar una diferencia con respecto al promedio anterior.

Respuesta:: \(\overline{X}\)= 9.44,\(s\) = 0.35,\(s_{\overline{X}}\) = 0.06,\(df\) = 36,\(t*\) = 2.719, IC 99% = (9.28, 9.60); CI no se corchete\(μ\), rechaza hipótesis nula. \(d\)= 1.83

Determine si rechazaría o no rechazaría la hipótesis nula en las siguientes situaciones:
1. \(t\)= 2.58,\(N\) = 21, prueba de dos colas a\(α\) = 0.05
2. \(t\)= 1.99,\(N\) = 49, prueba de una cola a\(α\) = 0.01
3. \(μ\)= 47.82, IC 99% = (48.71, 49.28)
4. \(μ\)= 0, IC 95% = (-0.15, 0.20)
Tienes curiosidad sobre cómo se siente la gente acerca de la cerveza artesanal, por lo que recopilas datos de 55 personas en la ciudad sobre si les gusta o no. Codificas tus datos para que 0 sea neutral, las puntuaciones positivas indiquen que te gusta la cerveza artesanal, y las puntuaciones negativas indican que no le gusta la cerveza artesanal. Encuentras que la opinión promedio fue\(\overline{X}\) = 1.10 y el spread fue\(s\) = 0.40, y pruebas para una diferencia de 0 en el nivel\(α\) = 0.05.

Respuesta:

Paso 1:\(H_0: μ = 0\) “La persona promedio tiene una opinión neutral hacia la cerveza artesanal”,\(H_A: μ ≠ 0\) “En general la gente tendrá una opinión sobre la cerveza artesanal, ya sea buena o mala”.

Paso 2: Prueba de dos colas,\(df\) = 54,\(t*\) = 2.009.

Paso 3:\(\overline{X}\) = 1.10,\(s_{\overline{X}}\) = 0.05,\(t\) = 22.00.

Paso 4:\(t > t*\), Rechazar\(H_0\).

Con base en opiniones de 55 personas, podemos concluir que la opinión promedio de la cerveza artesanal (\(\overline{X}\)= 1.10) es positiva,\(t(54)\) = 22.00,\(p\) < .05. Dado que el resultado es significativo, necesitamos un tamaño de efecto: Cohen\(d\) = 2.75, que es un efecto grande.

Quieres saber si los universitarios tienen más estrés en su vida diaria que la población general (\(μ\)= 12), por lo que recopilas datos de 25 personas para poner a prueba tu hipótesis. Su muestra tiene una puntuación de estrés promedio de\(\overline{X}\) = 13.11 y una desviación estándar de\(s\) = 3.89. Use una\(t\) prueba de 1 muestra para ver si hay alguna diferencia.