5.2: Probabilidad en Gráficas y Distribuciones
- Page ID
- 150907
Veremos en breve que la distribución normal es la clave de cómo funciona la probabilidad para nuestros fines. Para entender exactamente cómo, primero veamos un ejemplo simple e intuitivo usando gráficos circulares.
Probabilidad en Pie
Gráficos Recordemos que un gráfico circular representa la frecuencia con la que se observó una categoría y que todos los sectores del gráfico circular suman el 100%, o 1. Esto significa que si seleccionamos aleatoriamente una observación a partir de los datos utilizados para crear el gráfico circular, la probabilidad de que tome un valor específico es exactamente igual al tamaño del sector de esa categoría en el gráfico circular.
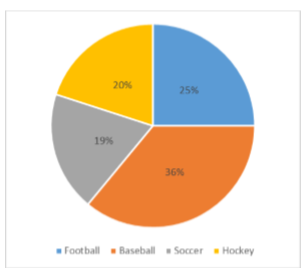
Tomemos, por ejemplo, el gráfico circular en Figura\(\PageIndex{1}\) que representa los deportes favoritos de 100 personas. Si pones este gráfico circular en un tablero de dardos y apuntas ciegamente (asumiendo que tienes la garantía de golpear el tablero), la probabilidad de golpear la rebanada para cualquier deporte dado sería igual al tamaño de esa rebanada. Entonces, la probabilidad de golpear la rebanada de béisbol es la más alta con 36%. La probabilidad es igual a la proporción del gráfico que ocupa esa sección.
También podemos agregar rebanadas juntas. Por ejemplo, tal vez queremos saber la probabilidad de encontrar a alguien cuyo deporte favorito se suele jugar sobre el césped. Los resultados que satisfacen este criterio son el béisbol, el fútbol y el fútbol. Para obtener la probabilidad, simplemente sumamos sus rebanadas juntas para ver qué proporción del área del gráfico circular se encuentra en esa región: 36% + 25% + 20% = 81%. También podemos sumar secciones aunque no se toquen. Si queremos saber la probabilidad de que el deporte favorito de alguien no se llame fútbol en algún lugar del mundo (es decir, béisbol y hockey), podemos sumar esas rebanadas aunque no sean adyacentes o continuas en la propia tabla: 36% + 20% = 56%. Somos capaces de hacer todo esto porque 1) el tamaño de la porción corresponde al área del gráfico ocupada por esa porción, 2) el porcentaje para una categoría específica se puede representar como un decimal (este paso se omitió para facilitar la explicación anterior), y 3) el área total del gráfico es igual al 100% o 1.0, lo que hace que el tamaño de las rebanadas sea interpretable.
Probabilidad en distribuciones normales
Si el lenguaje al final de la última sección sonaba familiar, eso es porque es exactamente el lenguaje utilizado en el último capítulo para describir la distribución normal. Recordemos que la distribución normal tiene un área bajo su curva que es igual a 1 y que se puede dividir en secciones dibujando una línea a través de ella que corresponde a una\(z\) puntuación dada. Debido a esto, podemos interpretar áreas bajo la curva normal como probabilidades que corresponden a\(z\) -scores.
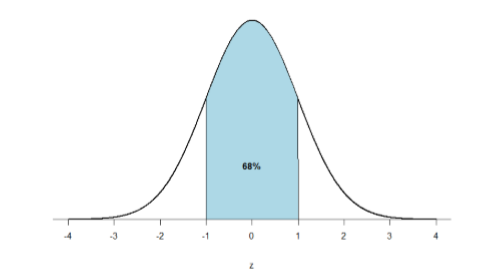
Primero, echemos un vistazo al área entre\(z\) = -1.00 y\(z\) = 1.00 presentada en la Figura\(\PageIndex{2}\). Nos dijeron antes que esta región contiene 68% del área bajo la curva. Así, si elegimos aleatoriamente una\(z\) puntuación -score de todas las puntuaciones z posibles, existe un 68% de probabilidad de que esté entre\(z\) = -1.00 y\(z\) = 1.00 porque esas son las\(z\) puntuaciones -que satisfacen nuestros criterios.
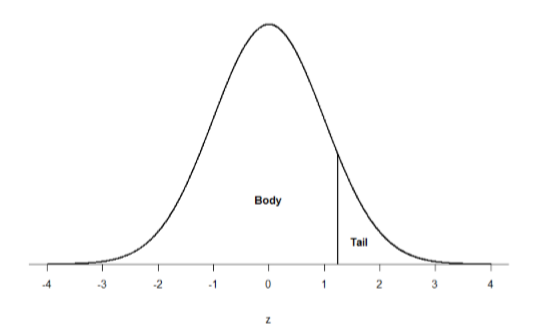
Así como un gráfico circular se divide en rebanadas dibujando líneas a través de él, también podemos dibujar una línea a través de la distribución normal para dividirlo en secciones. Eche un vistazo a la distribución normal en la Figura\(\PageIndex{3}\) que tiene una línea dibujada a través de ella como\(z\) = 1.25. Esta línea crea dos secciones de la distribución: la sección más pequeña llamada cola y la sección más grande llamada cuerpo. Diferenciar entre el cuerpo y la cola no depende de qué lado de la distribución se dibuje la línea. Todo lo que importa es el tamaño relativo de las piezas: más grande es siempre cuerpo.
Como puede ver, podemos dividir la distribución normal en 3 piezas (cola inferior, cuerpo y cola superior) como en la Figura\(\PageIndex{2}\) o en 2 piezas (cuerpo y cola) como en Figura\(\PageIndex{3}\). Luego podemos encontrar la proporción del área en el cuerpo y la cola en función de dónde se trazó la línea (es decir, a qué\(z\) puntaje). Matemáticamente esto se hace usando cálculo. Afortunadamente, se le dan los valores exactos en la Tabla de Distribución Normal Estándar, también conocida en la\(z\) tabla -. Usando los valores de esta tabla, podemos encontrar el área bajo la curva normal en cualquier cuerpo, cola o combinación de colas sin importar qué\(z\) puntuaciones se usen para definirlas.
La\(z\) tabla -presenta los valores para el área bajo la curva a la izquierda de las\(z\) puntuaciones positivas de 0.00-3.00 (técnicamente 3.09), como lo indica la región sombreada de la distribución en la parte superior de la tabla. Para encontrar el valor apropiado, primero encontramos la fila correspondiente a nuestro\(z\) -score y luego la seguimos hasta llegar a la columna que corresponde al número en el lugar de centésimas de nuestra\(z\) -score. Por ejemplo, supongamos que queremos encontrar el área en el cuerpo para una\(z\) -score de 1.62. Primero encontraríamos la fila para 1.60 luego la seguiríamos hasta la columna etiquetada 0.02 (1.60 + 0.02 = 1.62) y encontraríamos 0.9474 (ver Figura\(\PageIndex{4}\)). Así, las probabilidades de seleccionar aleatoriamente a alguien con un\(z\) puntaje -menor que (a la izquierda de)\(z\) = 1.62 es 94.74% porque esa es la proporción del área ocupada por valores que satisfacen nuestros criterios.
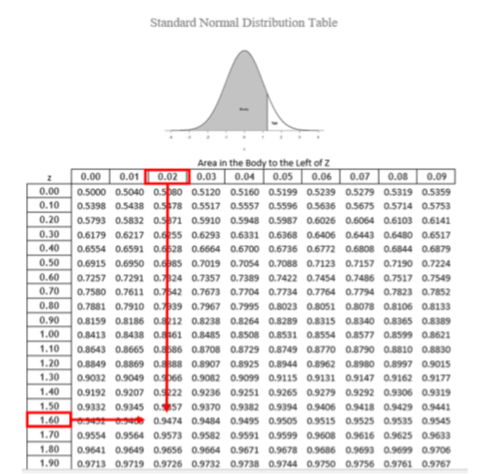
La\(z\) tabla -solo presenta el área en el cuerpo para\(z\) puntuaciones positivas porque la distribución normal es simétrica. Así, el área en el cuerpo de\(z\) = 1.62 es igual al área en el cuerpo para\(z\) = -1.62, aunque ahora el cuerpo será el área sombreada a la derecha de\(z\) (porque el cuerpo siempre es más grande). En caso de duda, dibujar tu distribución y sombrear el área que necesitas encontrar siempre te ayudará. El cuadro también solo presenta el área en el cuerpo porque el área total bajo la curva normal siempre es igual a 1.00, así que si necesitamos encontrar el área en la cola para\(z\) = 1.62, simplemente encontramos el área en el cuerpo y la restamos de 1.00 (1.00 — 0.9474 = 0.0526).
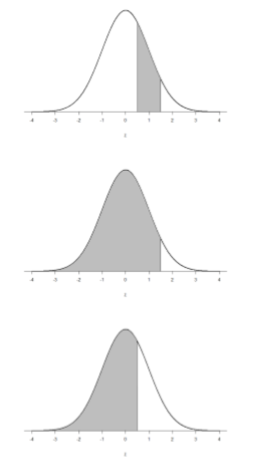
Veamos otro ejemplo. Esta vez, vamos a encontrar el área correspondiente a\(z\) -puntuaciones más extremas que\(z\) = -1.96 y\(z\) = 1.96. Es decir, vamos a encontrar el área en las colas de la distribución para valores menores que\(z\) = -1.96 (más negativos y por lo tanto más extremos) y mayores que\(z\) = 1.96 (más positivos y por lo tanto más extremos). Esta región se ilustra en la Figura\(\PageIndex{5}\).
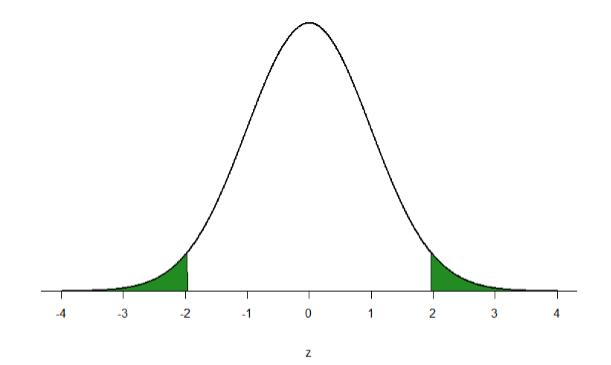
Empecemos con la cola para\(z\) = 1.96. Si vamos a la\(z\) -tabla encontraremos que el cuerpo a la izquierda de\(z\) = 1.96 es igual a 0.9750. Para encontrar el área en la cola, restamos eso de 1.00 para obtener 0.0250. Debido a que la distribución normal es simétrica, el área en la cola para\(z\) = -1.96 es exactamente el mismo valor, 0.0250. Por último, para obtener el área total en la región sombreada, simplemente sumamos las áreas para obtener 0.0500. Así, existe un 5% de probabilidad de obtener aleatoriamente un valor más extremo que\(z\) = -1.96 o\(z\) = 1.96 (este valor y región en particular se volverán increíblemente importantes en la Unidad 2).
Finalmente, podemos encontrar el área entre dos\(z\) puntuaciones sombreando y restando. La figura\(\PageIndex{6}\) muestra el área entre\(z\) = 0.50 y\(z\) = 1.50. Debido a que esta es una subsección de un cuerpo (en lugar de solo un cuerpo o una cola), primero debemos encontrar el mayor de los dos cuerpos, en este caso el cuerpo para\(z\) = 1.50, y restar el menor de los dos cuerpos, o el cuerpo para\(z\) = 0.50. Alinear las distribuciones verticalmente, como en la Figura 6, lo hace más claro. De la tabla z, el área en el cuerpo para\(z\) = 1.50 es 0.9332 y el área en el cuerpo para\(z\) = 0.50 es 0.6915. Restar estos nos da 0.9332 — 0.6915 = 0.2417.