4: Teoría inferencial
- Page ID
- 150369
Antes de las elecciones, los encuestadores encuestarán aproximadamente a 1000 personas y sobre la base de sus resultados, tratarán de predecir el resultado de la elección. En la superficie, debería parecer un absurdo que las opiniones de 1000 puedan dar algún indicio sobre la opinión de 100 mil millones de votantes en una elección presidencial nacional. De igual manera, tomar 100 o 1000 muestras de agua del Puget Sound, cuando esa es una cantidad minúscula de agua en comparación con la cantidad total de agua que cambia constantemente en el Sonido, debería parecer insuficiente para tomar una decisión.
El objetivo de este capítulo es desarrollar la teoría que nos ayude a entender por qué un tamaño de muestra relativamente pequeño puede llevar a conclusiones sobre una población mucho mayor. La explicación es diferente para los datos categóricos y cuantitativos. Comenzaremos con datos categóricos.
El viaje que realizarás a través de esta sección tiene un destino final en la fórmula que en última instancia se utilizará para probar hipótesis. Si bien podrías estar dispuesto a aceptar la fórmula sin tomar el viaje, será el viaje el que le dé sentido a la fórmula. Debido a que los datos son estocásticos, es decir, están sujetos a aleatoriedad, la probabilidad juega un papel crítico en este viaje.
Nuestro viaje comienza con el concepto de inferencia. La inferencia significa que se utiliza una pequeña cantidad de información observada para sacar conclusiones generales. Por ejemplo, puede visitar un negocio y recibir un excelente servicio al cliente de donde inferir que este negocio se preocupa por sus clientes. La inferencia se utiliza cuando se prueba una hipótesis. Una pequeña cantidad de información, la muestra, se utiliza para sacar una conclusión, o inferir algo sobre toda la población.
La teoría comienza con encontrar la probabilidad de obtener una muestra en particular y finalmente termina con la creación de distribuciones de todos los resultados de la muestra que son posibles si la hipótesis nula es verdadera. Para cada paso del viaje de 7 pasos, se harán digresiones para conocer las reglas específicas de probabilidad que contribuyen a la teoría inferencial.
Antes de comenzar, es necesario aclarar alguna de la terminología que se utilizará. Independientemente de la pregunta que se haga, si produce datos categóricos, esos datos serán identificados genéricamente como un éxito o fracaso, sin utilizar esos términos en su manera habitual. Por ejemplo, un investigador que haga una hipótesis sobre la proporción de personas que están desempleadas consideraría ser un éxito desde el punto de vista estadístico, y ser empleado como un fracaso, aunque eso contradice la forma en que se ve en el mundo real. Así, el éxito son los valores de datos sobre los cuales se escriben las hipótesis y el fracaso es el valor de datos alterno.
Briefing 4.1 Autos autónomos
Google, así como la mayoría de las empresas de automóviles, están desarrollando autos autónomos. Estos autos autónomos no necesitarán tener conductor y se consideran menos propensos a estar en un accidente que los autos conducidos por humanos. Se espera que autos como estos estén disponibles para el público alrededor de los años 2020 — 2025. Hay muchas preguntas que deben ser respondidas antes de que estos autos estén disponibles. Una de esas preguntas es determinar quién es el responsable en caso de accidente. ¿Es responsable el dueño del auto, a pesar de que no estaban dirigiendo el auto o es el fabricante el responsable ya que su tecnología no evitó el accidente? (mashable.com/2014/07/07/drive... -coches-propina- punto/, visto julio 2014).
Paso 1 — ¿Qué tan probable es que un valor de datos en particular sea el éxito?
Supongamos que un investigador quería determinar la proporción del público que cree que el dueño es responsable del accidente. El investigador tiene la hipótesis de que la proporción es superior al 60%. En este caso, las hipótesis serán:
- \(H_0: p = 0.60\)
- \(H_1: p > 0.60\)
Al recabar datos, el orden en que se seleccionan las unidades o personas determina el orden en que se recogen los datos. En este caso, la asignación de responsabilidad al propietario se considerará un éxito y la asignación de responsabilidad al fabricante se considera un fracaso. Si la primera persona cree que el propietario es responsable, la segunda persona cree que el fabricante es responsable, la tercera persona selecciona al fabricante, la cuarta, quinta y sexta personas seleccionan al propietario como la parte responsable, entonces podemos convertir esta información en éxitos y fracasos listando el orden en que se obtuvieron los datos como SFFSSS.
La estrategia que se emplea para determinar cuál de las dos hipótesis competidoras está mejor sustentada es siempre asumir que la hipótesis nula es verdadera. Este es un punto crítico, porque si podemos asumir que una condición es verdadera, entonces podemos determinar la probabilidad de obtener nuestro resultado de muestra particular, o resultados más extremos. Este es un valor p.
Sin embargo, antes de poder determinar la probabilidad de obtener una secuencia como SFFSSS, primero debemos encontrar la probabilidad de obtener un éxito. Para ello, necesitamos explorar el concepto de probabilidad.
Digresión 1 — Probabilidad
La probabilidad es la posibilidad de que ocurra un resultado en particular si un proceso se repite un número muy grande de veces. Se cuantifica dividiendo el número de resultados favorables por el número de posibles resultados. Esto se muestra como una fórmula:
\[P(A) = \dfrac{\text{Number of Favorable Outcomes}}{\text{Number of Possible Outcomes}}\]
donde\(P(A)\) significa la probabilidad de algún evento llamado\(A\). Esta fórmula supone que todos los resultados son igualmente probables, que es lo que sucede con un buen proceso de muestreo aleatorio. Todo el conjunto de posibles resultados se llama espacio muestral. El número de posibles resultados es el mismo que el número de elementos en el espacio muestral.
Si bien la intención de este capítulo es enfocarse en desarrollar la teoría para probar hipótesis, algunos conceptos serán explicados inicialmente con ejemplos más fáciles.
Si quisiéramos saber la probabilidad de obtener una cola cuando volteamos una moneda justa, entonces primero debemos considerar el espacio muestral, que sería {H, T}. Dado que hay un elemento en ese espacio muestral que es favorable y el espacio muestral contiene dos elementos, la probabilidad es\(p(tails) = \dfrac{1}{2}\).
Para encontrar la probabilidad de obtener un 4 al enrollar una matriz justa, creamos el espacio de muestra con seis elementos {1,2,3,4,5,6}, ya que estos son los posibles resultados que se pueden obtener al rodar la matriz. Para encontrar la probabilidad o rodando un 4, podemos sustituir en la fórmula para obtener\(P(4) = \dfrac{1}{6}\).
Una pregunta más desafiante es determinar la probabilidad de obtener dos cabezas al voltear dos monedas o voltear una moneda dos veces. El espacio muestral para este experimento es {HH, HT, TH, TT}. La probabilidad es (HH) =\(\dfrac{1}{4}\). La probabilidad de obtener una cabeza y una cola, en cualquier orden es (1 cabeza y 1 cola) =\(\dfrac{2}{4}\) =\(\dfrac{1}{2}\).
La probabilidad siempre será un número entre 0 y 1, así\(0 \le P(A) \le 1\). Una probabilidad de 0 significa que algo no puede suceder. Una probabilidad de 1 es una certeza.
Aplicar este concepto de probabilidad a la hipótesis sobre la responsabilidad de un auto autónomo en un accidente.
Si asumimos que la hipótesis nula es cierta, entonces la proporción de personas que creen que el dueño es responsable es 0.60. ¿Qué significa eso? Significa que si hay exactamente 100 personas, entonces exactamente 60 de ellas responsabilizan al dueño y 40 de ellas no.
Si nuestro objetivo es encontrar la probabilidad de SFFSSS, entonces primero debemos encontrar la probabilidad de conseguir un éxito (propietario). Si hay 100 personas en la población y 60 de estas seleccionan al propietario, entonces la probabilidad de seleccionar a una persona que elija al dueño es\(P(owner) = \dfrac{60}{100} = 0.60\). Observe que esta probabilidad es exactamente igual a la proporción definida en la hipótesis nula. Esto no es una coincidencia y sucederá cada vez porque la proporción en la hipótesis nula se utiliza para generar una población teórica, la cual se utilizó para encontrar la probabilidad. El primer paso importante en el proceso de prueba de una hipótesis es darse cuenta de que la probabilidad de que algún dato sea un éxito es igual a la proporción definida en la hipótesis nula, asumiendo que el muestreo se realiza con reemplazo, o que el tamaño de la población es extremadamente grande para que se elimine un unidad de la población no cambia la probabilidad una cantidad significativa.
Ejemplo 1
- Si\(H_0: p = 0.35\), entonces la probabilidad de que el\(5^{\text{th}}\) valor sea un éxito es 0.35.
- Si\(H_0: p = 0.82\), entonces la probabilidad de que el\(20^{\text{th}}\) valor sea un éxito es 0.82.
Paso 2 - ¿Qué tan probable es que un valor de datos en particular sea un fallo?
Ahora que sabemos encontrar la probabilidad de éxito, debemos encontrar la probabilidad de fracaso. Para ello, volveremos a desviarnos a las reglas de probabilidad.
Digresión 2 - Probabilidad de A o B
Cuando se selecciona una unidad de una población, puede haber varias medidas posibles que se pueden tomar sobre ella. Por ejemplo, una nueva pieza de tecnología podría colocarse en varias marcas de automóviles y luego probarse para determinar su confiabilidad. La tabla de contingencia a continuación muestra el número de autos en cada una de las categorías. Estos números son ficticios y vamos a pretender que es toda la población de autos en desarrollo.
| Hyundai | Nissan | Total | ||
|---|---|---|---|---|
| Confiable | 80 | 75 | 90 | 245 |
| No confiable | 25 | 10 | 20 | 55 |
| Total | 105 | 85 | 110 | Total total 300 |
A partir de esto podemos hacer una variedad de preguntas de probabilidad.
Si se selecciona al azar un automóvil, ¿cuál es la probabilidad de que sea un Nissan?
\(P(Nissan) = \dfrac{85}{300} = 0.283\)
Si se selecciona aleatoriamente un automóvil, ¿cuál es la probabilidad de que la pieza de tecnología no sea confiable?
\(P(not reliable) = \dfrac{55}{300} = 0.183\)
Si se selecciona al azar un automóvil, ¿cuál es la probabilidad de que sea un Hyundai o que la pieza de tecnología sea confiable?
Esta pregunta introduce la palabra “o” lo que significa que el automóvil tiene una característica u otra característica o ambas. La palabra “o” se utiliza cuando sólo se realiza una selección. La siguiente tabla debería ayudarle a entender cómo se derivará la fórmula.

Observe que los 2 valores en la columna Hyundai están marcados en un círculo y los tres valores en la fila de Confiables están en un círculo, pero que el valor en la celda que contiene el número 80 que representa el Hyundai y el Reliable se circunda dos veces. No queremos contar esos autos en particular dos veces así que después de sumar la columna para Hyundai a la fila para Confiable, es necesario restar la celda para Hyundai y Confiable porque se contabilizó dos veces pero solo se debe contar una vez. Así, la ecuación se convierte en:
P (Hyundai o Confiable) = P (Hyundai) + P (Confiable) — P (Hyundai y Confiable)
=\(\dfrac{105}{300} + \dfrac{245}{300} - \dfrac{80}{300} = \dfrac{270}{300} = 0.90\)
A partir de esto generalizaremos la fórmula para ser
\[P(A\ or\ B) = P(A) + P(B) - P(A\ and\ B).\]
¿Qué sucede si usamos la fórmula para determinar la probabilidad de seleccionar aleatoriamente un Nissan o un auto de Google?
Debido a que estos dos criterios no pueden darse ambos al mismo tiempo, se dice que son mutuamente excluyentes. En consecuencia, su intersección es 0.
P (Nissan o Google) = P (Nissan) + P (Google) — P (Nissan y Google)
=\(\dfrac{85}{300} + \dfrac{110}{300} - \dfrac{0}{300} = \dfrac{195}{300} = 0.65\)
Debido a que la intersección es 0, esto lleva a una fórmula modificada para valores de datos categóricos que son mutuamente excluyentes.
\[P(A\ or\ B) = P(A) + P(B)\]
Esta es la fórmula que nos interesa primordialmente para determinar cómo encontrar la probabilidad de fracaso.
Si el éxito y el fracaso son los dos únicos resultados posibles, y no es posible tener simultáneamente éxito y fracaso, entonces son mutuamente excluyentes. Además, si se realiza una selección aleatoria, entonces es seguro que será un éxito o un fracaso. Las cosas que son ciertas tienen una probabilidad de 1. Por lo tanto, podemos escribir la fórmula usando S y F como:
\(P(S\ or\ F) = P(S) + P(F)\)
o
\(1 = P(S) + P(F)\)
con un poco de álgebra esto se convierte
\[1- P(S) = P(F)\]
Lo que esto significa es que restar la probabilidad de éxito de 1 da la probabilidad de fracaso. La probabilidad de fracaso se llama el complemento de la probabilidad de éxito.
Aplicar este concepto de probabilidad a la hipótesis sobre la responsabilidad de un auto autónomo en un accidente.
Recordemos que la hipótesis original de la responsabilidad en un accidente es que: H0: p = 0.60. Hemos establecido que la probabilidad de éxito es de 0.60. La probabilidad de fracaso es de 0.40 ya que es el complemento de la probabilidad de éxito y 1 — 0.60 = 0.40.
Ejemplo 2
- Si\(H_0: p = 0.35\), entonces la probabilidad de que el\(5^{\text{th}}\) valor sea un éxito es 0.35. La probabilidad de que el\(5^{\text{th}}\) valor sea un fallo es 0.65.
- Si\(H_0: p = 0.82\), entonces la probabilidad de que el\(20^{\text{th}}\) valor sea un éxito es 0.82. La probabilidad de que el\(20^{\text{th}}\) valor sea un fallo es 0.18.
Paso 3 - ¿Qué tan probable es que una muestra consista en una secuencia específica de éxitos y fracasos?
Ahora sabemos que la probabilidad de éxito es idéntica a la proporción definida por la hipótesis nula y la probabilidad de fracaso es el complemento. Pero estas probabilidades se aplican a una sola selección. ¿Qué sucede cuando se selecciona más de uno? Para encontrar esa probabilidad, debemos aprender la última de las reglas de probabilidad:
\[P(A\ and\ B) = P(A)P(B)\]
Digresión 3 - P (A y B) = P (A) P (B)
Si se hacen dos o más selecciones, la palabra “y” se vuelve importante porque indica que estamos buscando un resultado para la primera selección y un resultado para la segunda selección. Esta probabilidad se encuentra multiplicando las probabilidades individuales. Parte de la clave para elegir esta fórmula es identificar el problema como un problema “y”. Por ejemplo, a principios de este capítulo encontramos que la probabilidad de obtener dos cabezas al voltear dos monedas es de 0.25. Este problema puede ser visto como un problema “y” si nos preguntamos “¿cuál es la probabilidad de obtener una cabeza en la primera vuelta y una cabeza en la segunda vuelta”? Usando subíndices de 1 y 2 para representar los volteos primero y segundo respectivamente, podemos reescribir la fórmula para mostrar:
\(P(H_1\ and\ H_2) = P(H_1)P(H_2) = (\dfrac{1}{2})(\dfrac{1}{2}) = \dfrac{1}{4} = 0.25.\)
Supongamos que el investigador selecciona al azar tres autos. ¿Cuál es la probabilidad de que haya un auto de cada una de las marcas (Hyundai, Nissan, Google)?
| Hyundai | Nissan | Total | ||
|---|---|---|---|---|
| Confiable | 80 | 75 | 90 | 245 |
| No confiable | 25 | 10 | 20 | 55 |
| Total | 105 | 85 | 110 | Total total 300 |
Primero, dado que se están seleccionando tres autos, esto debe reconocerse como un problema “y” y puede formularse P (Hyundai y Nissan y Google). Sin embargo, antes de que podamos determinar la probabilidad, hay una pregunta importante que debe hacerse. Esa pregunta es si el investigador seleccionará con reemplazo.
Si el investigador está muestreando con reemplazo, entonces la probabilidad se puede determinar de la siguiente manera.
P (Hyundai y Nissan y Google) = P (Hyundai) P (Nissan) P (Google) =
\((\dfrac{105}{300})(\dfrac{85}{300})(\dfrac{110}{300}) = 0.03636.\)
Observe el ligero cambio en la probabilidad como resultado de no usar reemplazo.
Aplicar este concepto de probabilidad a la hipótesis sobre la responsabilidad de un auto autónomo en un accidente.
Ahora estamos listos para responder a la pregunta de cuál es la probabilidad de que obtengamos la secuencia exacta de personas si la primera persona cree que el dueño es responsable, la segunda persona cree que el fabricante es responsable, la tercera persona selecciona al fabricante, la cuarta, quinta y sexta personas todas seleccionar al propietario como responsable. Debido a que hay seis personas seleccionadas, entonces esto es un problema “y” y puede escribirse como P (S y F y F y S y S y S) o de manera más concisa, dejando fuera la palabra “y” pero conservándola por implicación, escribimos P (SFFSSS). Recuerda que P (S) = 0.6 y P (F) = 0.4
P (SFFSSS) = P (S) P (F) P (F) P (S) P (S) P (S) = (0.6) (0.4) (0.4) (0.6) (0.6) = 0.0207.
Para resumir, si la hipótesis nula es cierta, entonces el 60% de la gente cree que el dueño es responsable de los accidentes. En estas condiciones, si se toma una muestra de seis personas, con reemplazo, entonces la probabilidad de obtener esta secuencia exacta de éxitos y fracasos es de 0.0207.
Paso 4 - ¿Qué tan probable es que una muestra contenga un número específico de éxitos?
Conocer la probabilidad de una secuencia exacta de éxitos y fracasos no es particularmente importante por sí mismo. Es un escalón hacia una cuestión de mayor importancia — ¿cuál es la probabilidad de que cuatro de cada seis personas seleccionadas al azar (con reemplazo) crean que el dueño es responsable? Esta es una importante transición en el pensamiento que se está haciendo. Es la transición de pensar en una secuencia específica a pensar en el número de éxitos en una muestra.
Cuando se recolectan los datos, a los investigadores no les importa el orden de los datos, solo cuántos éxitos hubo en la muestra. Necesitamos encontrar una manera de pasar de la probabilidad de obtener una secuencia particular de éxitos y fracasos como SFFSSS a encontrar la probabilidad de obtener cuatro éxitos de una muestra de tamaño 6. Esta transición hará uso de la propiedad conmutativa de multiplicación, la regla P (A o B) y combinatoria (métodos de conteo).
Al final del Paso 3 encontramos que P (SFFSSS) = 0.0207.
- ¿Cuál crees que será la probabilidad de P (SSSFSF)?
- ¿Cuál crees que será la probabilidad de P (SSSSFF)?
La respuesta a ambas preguntas es 0.0207 porque todas estas secuencias contienen 4 éxitos y dos fracasos y ya que la probabilidad se encuentra multiplicando las probabilidades de éxito y fracaso en secuencia y ya que la multiplicación es conmutativa (el orden no importa) entonces
(0.6) (0.4) (0.4) (0.6) (0.6) (0.6) = (0.6) (0.6) (0.6) (0.4) (0.6) (0.4) = (0.6) (0.6) (0.6) (0.6) (0.4) = 0.020736.
Si la pregunta ahora cambia de cuál es la probabilidad de una secuencia a cuál es la probabilidad de 4 éxitos en una muestra de tamaño 6, entonces tenemos que considerar todas las diferentes formas en que se pueden organizar cuatro éxitos. Podríamos obtener 4 éxitos si la secuencia de nuestra selección es SFFSSS o SSSFSF o SSSSFF o muchas otras posibilidades. Debido a que estamos muestreando una vez y porque hay muchos resultados posibles que podríamos tener, este es un problema “o” que utiliza una versión ampliada de la fórmula P (A o B) = P (A) + P (B). Esto se puede escribir como:
P (4 de 6) = P (SFFSSS o SSSFSF o SSSSFF o...) = P (SFFSSS) + P (SSSFSF) + P (SSSSFF) +...
Es decir, podemos sumar la probabilidad de cada una de estas órdenes. No obstante, dado que la probabilidad de cada una de estas órdenes es la misma (0.0207) entonces este proceso sería mucho más rápido si simplemente multiplicamos 0.0207 por el número de órdenes que son posibles. La pregunta que debemos responder entonces es ¿cuántas formas hay de arreglar cuatro éxitos y 2 fracasos? Para responder a esto, debemos explorar el campo de la combinatoria, que proporcionan diversos métodos de conteo.
Digresión 4 — Combinatoria
Los investigadores que diseñen los autos compararán diferentes tecnologías para ver cuál funciona mejor. Supongamos que dos marcas de una cámara de video están disponibles para un automóvil. ¿Cuántos pares diferentes son posibles?
Un diagrama de árbol puede ayudar a explicar esto.
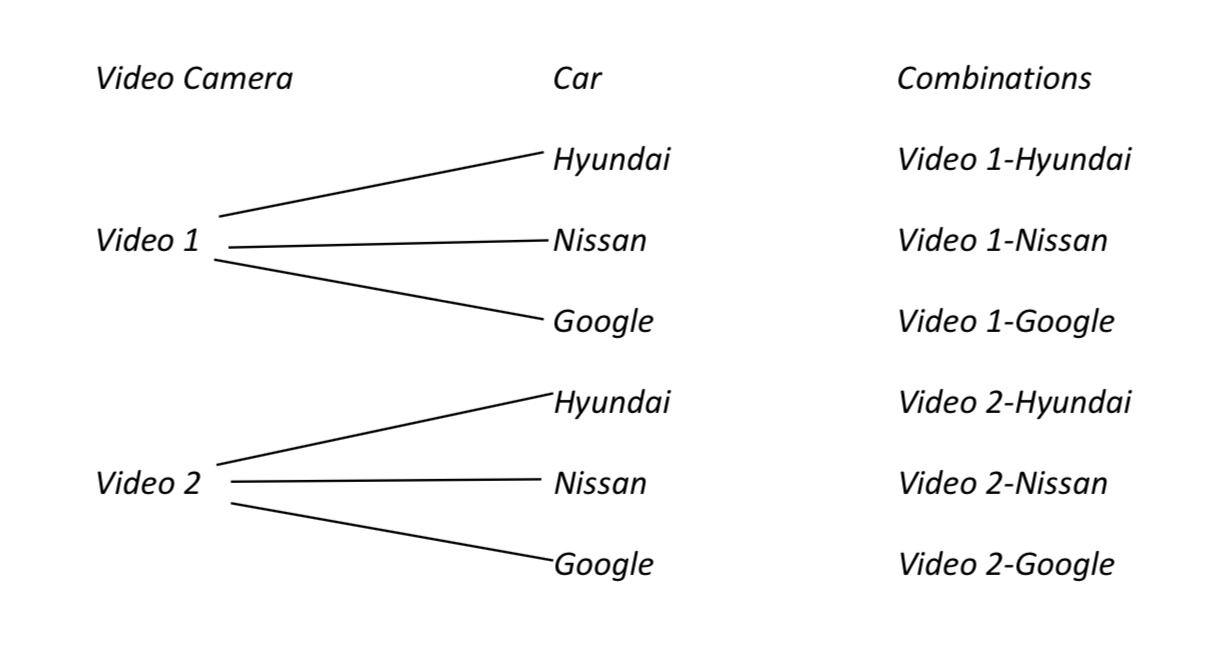
Hacer un diagrama de árbol para responder preguntas como esta puede ser tedioso, por lo que un enfoque más fácil es usar la regla fundamental de conteo que establece que si hay M opciones para una elección que debe hacerse y N opciones para una segunda elección que debe hacerse, entonces hay MN combinaciones únicas. Una forma de mostrar esto es dibujar y etiquetar una línea para cada elección que se debe hacer y en la línea escribir el número de opciones que están disponibles. Multiplique los números.
_______2_________ ________3_________ = 6
Videos Autos
Esto te dice que hay seis combinaciones únicas para una cámara y una marca de auto.
Si los investigadores tienen 4 vehículos de prueba que circularán en la autopista como convoy y los colores de los vehículos son azul, rojo, verde y amarillo, ¿de cuántas formas se pueden ordenar estos autos en el convoy?
Para responder a esta pregunta, piensa en ella como tener que tomar cuatro elecciones, qué color de auto es primero, segundo, tercero, cuarto. Dibuja una línea para cada elección y en la línea escribe el número de opciones que están disponibles y luego multiplica estos números. Hay cuatro opciones para el primer auto. Una vez que se hace esa elección quedan tres opciones para el segundo automóvil. Cuando se hace esa elección, quedan dos opciones para el tercer auto. Después de que se haga esa elección, solo hay una opción disponible para el auto final.
4 3 2 1 = 24 pedidos únicos
Primer Auto Segundo Auto Tercer Auto Cuarto Auto
Ejemplos de algunos de estos pedidos únicos incluyen: azul, rojo, verde y amarillo
rojo, azul, verde y amarillo
verde, rojo, azul y amarillo
Cada secuencia única se llama permutación. Así, en esta situación, hay 24 permutaciones.
La forma de encontrar el número de permutaciones cuando se utilizan todos los elementos disponibles se llama factorial. En este problema, se utilizan los cuatro autos, por lo que el número de permutaciones es de 4 factoriales que se muestra simbólicamente como ¡4!. ¡4! significa (4) (3) (2) (1). Para ser más generales,
\[n! = n(n - 1)(n - 2)... 1\]
También se pueden encontrar permutaciones cuando se utilizan menos elementos de los disponibles. Por ejemplo, supongamos que los investigadores sólo utilizarán dos de los cuatro autos. ¿Cuántos pedidos diferentes son posibles? Por ejemplo, el auto azul seguido por el auto verde es un orden diferente al auto verde seguido por el auto azul. Podemos responder a esta pregunta de dos maneras (¡y ojalá obtengamos la misma respuesta en ambos sentidos!). La primera forma es usar la regla fundamental de conteo y dibujar dos líneas para las elecciones que hacemos, poniendo el número de opciones disponibles para cada elección en la línea y luego multiplicando.
4 3 = 12 permutaciones
Primer Auto Segundo Auto
Ejemplos de posibles permutaciones incluyen:
Azul, Verde, Verde, Azul, Azul, Rojo Amarillo, Verde
El segundo enfoque es usar la fórmula para permutaciones cuando el número seleccionado es menor o igual al número de disponibles. En esta fórmula, r representa el número de elementos seleccionados, n representa el número de elementos disponibles.
\[nPr = \dfrac{n!}{(n - r)!}\]
Para este ejemplo, n es 4 y r es 2 así que con la fórmula obtenemos:
\(_4P_2 = \dfrac{4!}{(4 - 2)!} = \dfrac{4!}{2!} = \dfrac{4 \cdot 3 \cdot 2 \cdot 1}{2 \cdot 1} = 4 \cdot 3 = 12\)permutaciones.
Observe que el producto final de\(4 \cdot 3\) es el mismo que tenemos al usar la regla fundamental de conteo. El término denominador de (n-r)! se utiliza para cancelar los términos innecesarios del numerador.
Para las permutaciones, el orden es importante, pero ¿y si el orden no es importante? Por ejemplo, y si quisiéramos saber cuántos pares de autos de diferentes colores podrían combinarse si no nos importaba el orden en el que conducían. En tal caso, nos interesan las combinaciones. Mientras que el Azul, el Verde y el Verde, el Azul representan dos permutaciones, representan solo una combinación. Siempre habrá más permutaciones que combinaciones. El número de permutaciones para cada combinación es r!. Es decir, cuando se seleccionan 2 autos ¡hay 2! permutaciones para cada combinación.
Para determinar el número de combinaciones hay si se seleccionan dos de los cuatro autos podemos dividir el número total de permutaciones por el número de permutaciones por combinación.
\(Number\ of\ combinations = Number\ of\ permutations (\dfrac{1\ Combination}{Number\ of\ Permutations})\)
Usando notación similar a la utilizada para las permutaciones (nPr), las combinaciones se pueden representar con nCr, por lo que la ecuación se puede reescribir como
\[\begin{array} {rcl} {nCr} &= & {nPr(\dfrac{1}{r!})\ or} \\ {nCr} &= & {\dfrac{n!}{(n - r)!} (\dfrac{1}{r!})} \\ {nCr} &= & {\dfrac{n!}{(n - r)!r!}} \end{array}\]
Una forma alternativa de desarrollar esta fórmula que podría usarse para tamaños de muestra más grandes que contengan éxitos y fracasos es considerar que el número de permutaciones es n! mientras que el número de permutaciones para cada combinación es r! (n-r)!. Por ejemplo, en una muestra de talla 20 con 12 éxitos y 8 fracasos, ¡hay 20! permutaciones de los éxitos y fracasos combinados con 12! permutaciones de éxitos y ¡8! permutaciones de fallas para cada combinación. Por lo tanto,
\(Number\ of\ combinations = 20!(\dfrac{1\ Combination}{12!8!}) = \dfrac{20!}{12!8!}\ or\ as\ a\ formula:\)
\(Number\ of\ combinations = n!(\dfrac{1\ Combination}{r!(n - r)!}) = \dfrac{n!}{r!(n - r)!}\ or\ \dfrac{n!}{(n - r)!r!}\).
Para nuestro ejemplo sobre los colores de los autos tenemos:
\(_4C_2 = \dfrac{4!}{(4 - 2)! 2!} = \dfrac{4 \cdot 3 \cdot 2 \cdot 1}{2 \cdot 1 \cdot 2 \cdot 1} = 6\)combinaciones.
Esta secuencia de conceptos combinatorios ha alcanzado el objetivo pretendido en que el interés está en el número de combinaciones de éxitos y fracasos que hay para un número dado de éxitos en una muestra. Ahora volveremos al problema de la responsabilidad por los accidentes.
Aplicar este concepto de probabilidad a la hipótesis sobre la responsabilidad de un auto autónomo en un accidente.
Recordemos que se seleccionaron 6 personas y 4 pensaban que el dueño debería ser responsable. Vimos que la probabilidad de cualquier secuencia de 4 éxitos y 2 fracasos, como SFFSSS o SSSFSF o SSSSFF es 0.0207 si la hipótesis nula es p = 0.60. Si conociéramos el número de combinaciones de estos 4 éxitos y 2 fracasos, podríamos multiplicar ese número por la probabilidad de cualquier secuencia específica para obtener la probabilidad de 4 éxitos en una muestra de tamaño 6.
Usando la fórmula para nCr, obtenemos:\(_6C_4 = \dfrac{6!}{(6 - 4)!4!} = 15\) combinaciones.
Por lo tanto, la probabilidad de 4 éxitos en una muestra de tamaño 6 es 15*0.020736 = 0.31104. Esto quiere decir que si la hipótesis nula de p=0.60 es cierta y se le pregunta a seis personas, existe una probabilidad de 0.311 de que cuatro de esas personas crean que el dueño es responsable.
Ahora estamos listos para hacer la transición a las distribuciones. En la siguiente tabla se resume nuestro recorrido hasta este punto.
| Paso 1 | Utilice la hipótesis nula para determinar P (S) para cualquier selección, asumiendo la sustitución. |
| Paso 2 | Usa la regla P (A o B) para encontrar el complemento, que es la P (F) = 1 - P (S) |
| Paso 3 | Utilice la regla P (A o B) para encontrar la probabilidad de una secuencia específica de una secuencia específica de éxitos y fracasos, como SFFSSS, multiplicando las probabilidades individuales. |
| Paso 4 | R ecognizar que todas las combinaciones de r éxitos de una muestra de tamaño n tienen la misma probabilidad de ocurrir. Encuentra el número de combinaciones nCr y multiplica esto por la probabilidad de cualquiera de las combinaciones para determinar la probabilidad de obtener r éxitos de una muestra de tamaño n. |
Paso 5 — ¿Cómo se puede encontrar el valor p exacto usando la distribución binomial?
Recordemos que en el capítulo 2, determinamos qué hipótesis se sustentó al encontrar el valor p. Si el valor p era pequeño, menor que el nivel de significancia, concluimos que los datos apoyaban la hipótesis alternativa. Si el valor p era mayor que el nivel de significancia, concluimos que los datos apoyaban la hipótesis nula. El valor p es la probabilidad de obtener los datos, o datos más extremos, asumiendo que la hipótesis nula es verdadera.
En el Paso 4 encontramos la probabilidad de obtener los datos (por ejemplo, cuatro éxitos de 6) pero aún no hemos encontrado la probabilidad de obtener datos más extremos. Para ello, ahora debemos crear distribuciones. Una distribución muestra la probabilidad de todos los posibles resultados de un experimento. Para los datos categóricos, hacemos una distribución discreta.
Antes de mirar la distribución que es relevante para el problema de responsabilidad por accidentes, se brindará una discusión general de distribuciones.
En el capítulo 4 aprendiste a hacer histogramas. Los histogramas muestran la distribución de los datos. En el capítulo 4 también aprendiste sobre medias y desviaciones estándar. Las distribuciones también tienen medias y desviaciones estándar.
Para demostrar los conceptos, comenzaremos con un ejemplo sencillo. Supongamos que alguien tiene dos rutas utilizadas para correr. Una ruta tiene 2 millas de largo y la otra es de 5 millas de largo. A continuación se muestra el horario de ejecución de la semana pasada.
| domingo | Lunes | martes | Miércoles | jueves | Viernes | Sábado |
| 5 | 2 | 2 | 5 | 2 | 2 | 5 |
A continuación se muestra una distribución de la cantidad ejecutada cada día.
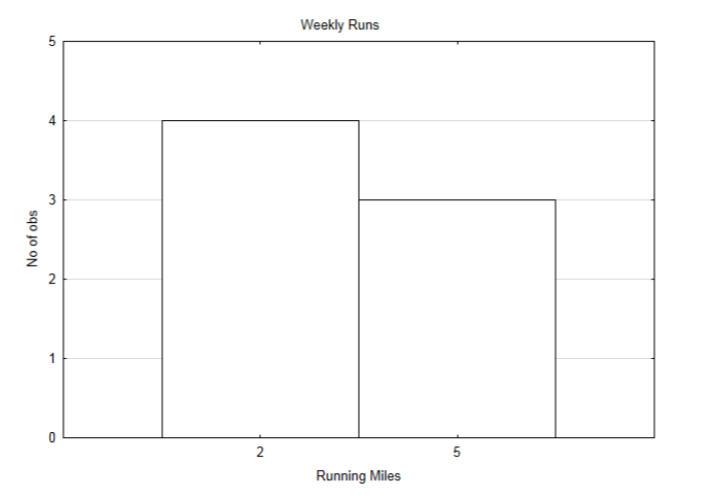
La media se puede encontrar sumando todas las corridas diarias y dividiendo por 7. La media es de 3.286 millas por día. Debido a que las mismas distancias se repiten en días diferentes, también se puede utilizar una media ponderada. En este caso, el peso es el número de veces que se corrió una distancia determinada. Una media ponderada aprovecha la multiplicación en lugar de la suma. Así, en lugar de calcular:\(\dfrac{2 + 2 + 2 + 2 + 5 + 5 + 5}{7} = 3.286\). podemos multiplicar cada número por el número de veces que ocurre luego dividir por el número de ocurrencias:\(\dfrac{4 \cdot 2 + 3 \cdot 5}{4 + 3} = 3.286\). La fórmula para una media ponderada es:
\[\dfrac{\sum w \cdot x}{\sum w}\]
A continuación se presenta la misma gráfica, pero esta vez hay porcentajes por encima de las barras.
En lugar de usar recuentos como peso, los porcentajes (en realidad las proporciones) se pueden usar como peso. Así 57.143% puede escribirse como 0.57143. De igual manera, 42.857% se puede escribir 0.42857.
Sustituir en la fórmula da:\(\dfrac{0.57143 \cdot 2 + 0.42857 \cdot 5}{0.57143 + 0.42857} = 3.286\). Observe que el denominador se suma a 1. Por lo tanto, si el peso es la proporción de veces que ocurre un valor, entonces la media de una distribución que usa porcentajes se puede encontrar usando la fórmula:
\[\mu = \sum P(x) x\]
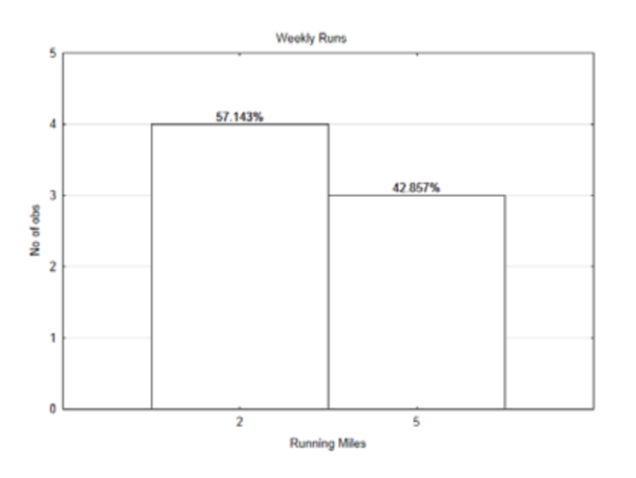
Esta media, que también se conoce como el valor esperado, es la suma de la probabilidad de un valor por el valor. No hay necesidad de dividir, como es costumbre a la hora de encontrar medios, porque siempre solo dividiríamos por 1.
Recordemos del capítulo 4 que la desviación estándar es la raíz cuadrada de la varianza. La varianza es\(\sigma^2 = \sum[(x - \mu)^2 \cdot P(x)]\). La desviación estándar es\(\sigma = \sqrt{\sum[(x - \mu)^2 \cdot P(x)]}\).
\(\sigma = \sqrt{\sum[(x - \mu)^2 \cdot P(x)]}\).
\(\sigma = \sqrt{(2 - 3.286)^2 \cdot 0.57143 + (5 - 3.286)^2 \cdot 0.42857} = 1.485\)
El problema del auto autónomo nos mostrará una forma en la que nos encontramos con distribuciones discretas. De hecho, resultará en la creación de un tipo especial de distribución discreta llamada distribución Binomial, que se definirá después de explorar los conceptos que conducen a su creación.
Al probar una hipótesis sobre proporciones de éxitos, hay dos variables aleatorias que nos interesan. La primera variable aleatoria es específica de los datos que recopilaremos. Por ejemplo, en la investigación sobre quién es responsable de los accidentes causados por autos autónomos, la variable aleatoria sería “parte responsable”. Habría dos valores posibles para esta variable aleatoria, propietario o fabricante de automóviles. Hemos estado considerando que el propietario es un éxito y el fabricante como un fracaso. Los datos que recogen los investigadores son sobre esta variable aleatoria. Sin embargo, crear distribuciones y encontrar probabilidades y valores p requiere un cambio de nuestro enfoque hacia una variable aleatoria diferente. Esta segunda variable aleatoria trata sobre el número de éxitos en una muestra de tamaño n. Es decir, si se pregunta a seis personas, ¿cuántas de ellas piensan que el dueño es responsable? Es posible que ninguno de ellos piense que el dueño es responsable, o uno piense que el dueño es responsable, o dos, o tres, o cuatro, o cinco, o los seis piensan que el dueño es responsable. Por lo tanto, en una muestra de tamaño 6, la variable aleatoria para el número de éxitos puede tener los valores de 0,1,2,3,4,5,6. Ya hemos encontrado que la probabilidad de obtener cuatro éxitos es de 0.3110. Ahora encontraremos la probabilidad de obtener 0,1,2,3,5,6 éxitos, asumiendo que las hipótesis siguen siendo\(H_0: p = 0.60\),\(H_1: p > 0.60\). Esto nos permitirá crear la distribución binomial discreta de todos los resultados posibles.
Encuentra la probabilidad de 0 éxitos
La única manera de tener 0 éxitos es tener todos los fracasos, así estamos buscando P (FFFFFF).
P (FFFFFF) = P (F) P (F) P (F) P (F) P (F) P (F) = (0.4) (0.4) (0.4) (0.4) (0.4) (0.4) = 0.004096.
Dado que solo hay una combinación para 0 éxitos, entonces la probabilidad de 0 éxitos es 0.0041.
Encuentra la probabilidad de 1 éxito
Sabemos que todas las combinaciones tienen la misma probabilidad, así que también podemos crear la combinación más simple para 1 éxito. Esto sería SFFFF.
P (SFFFFF) = P (S) P (F) P (F) P (F) P (F) P (F) = (0.6) (0.4) (0.4) (0.4) (0.4) (0.4) =\((0.6)^{1}(0.4)^{5}\) = 0.006144.
¿Cuántas combinaciones hay para 1 éxito? Esto se puede encontrar usando\(_6C_1\).
\(_6C_1 = \dfrac{6!}{(6 - 1)!1!} = 6\)combinaciones. ¿Esta respuesta parece razonable? Considera que sólo hay 6 lugares en los que el éxito podría suceder.
La probabilidad de 1 éxito es entonces 6*0.006144 = 0.036864 o si redondeamos a cuatro decimales, 0.0369.
Encuentra la probabilidad de 2 éxitos.
En lugar de hacer este problema en pasos como se hizo para los ejemplos anteriores, se demostrará combinando pasos.
\(_6C_2 P\)(SSFFFF)
\(\dfrac{6!}{(6 - 2)! 2!} (0.6)(0.6)(0.4)(0.4)(0.4)(0.4) = \dfrac{6!}{(6 - 2)! 2!} (0.6)^2(0.4)^4 =\)
15 (0.009216) = 0.13824 o con redondeo a cuatro decimales 0.1382.
Encuentra la probabilidad de 3 éxitos usando los pasos combinados. (Ahora es tu turno).
Encuentra la probabilidad de 5 éxitos.
Encuentra la probabilidad de 6 éxitos.
Cuando se hayan encontrado todas las probabilidades, podemos crear una tabla que muestre los valores que puede tomar la variable aleatoria y sus probabilidades. Definiremos las variables aleatorias para el número de éxitos como X con los valores posibles definidos como x.
| X = x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| P (X = x) | 0.0041 | 0.0369 | 0.1382 | 0.2765 | 0.3110 | 0.1866 | 0.0467 |
¿Tus valores para 3,5, y 6 éxitos concuerdan con los valores que se encuentran en la tabla?
Una gráfica de esta distribución puede conducir a una mejor comprensión de la misma. Esta gráfica se denomina función de masa de probabilidad, que se muestra usando un gráfico de barras. Es una forma de graficar distribuciones discretas, ya que no puede haber ningún valor entre los números en el eje x. Las alturas de la barra corresponden a la probabilidad de obtener el número de éxitos.
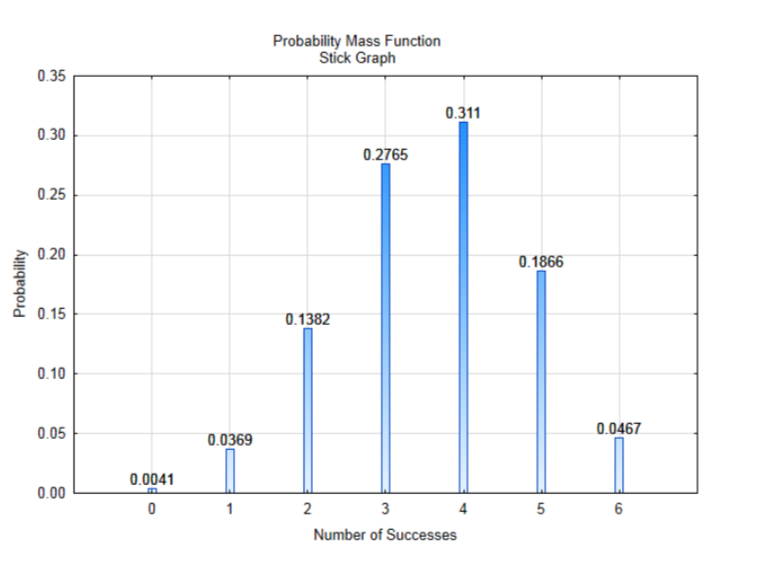
Hay tres cosas que debes notar sobre esta distribución. En primer lugar, se trata de una distribución completa. Es decir, en una muestra de tamaño seis, sólo es posible tener 0,1,2,3,4,5, o 6 éxitos y todos esos han sido incluidos en la gráfica. Lo segundo que hay que notar es que todas las probabilidades tienen valores entre 0 y 1. Esto debe esperarse porque las probabilidades deben estar siempre entre 0 y 1. Lo último a notar, que puede no ser obvio al principio, es que si se suman todas las probabilidades, la suma será 1. La suma de todas las distribuciones de probabilidad completas debe ser igual a 1,\(\sum P(x) =1\). Si agregas todas las probabilidades y no son iguales a una, sino que están muy cerca, podría ser por redondeo, no porque hiciste algo malo.
Digresión 5 - Distribuciones Binomiales
Todo el recorrido que se ha realizado desde el inicio de este capítulo ha llevado a la creación de una distribución discreta muy importante llamada distribución binomial, que tiene los siguientes componentes.
- Un Ensayo de Bernoulli es una muestra que sólo puede tener dos resultados posibles, el éxito y el fracaso.
- Un experimento puede consistir en n ensayos independientes de Bernoulli.
- Una Variable Aleatoria Binomial, X es el número de éxitos en un experimento
- Una Distribución Binomial muestra todos los valores para X y la probabilidad de que cada uno de esos valores ocurra.
Los supuestos son que:
- Todos los juicios son independientes.
- El número de ensayos en un experimento es el mismo y se define por la variable n.
- La probabilidad de éxito se mantiene constante para cada muestra. La probabilidad de fracaso es el complemento de la probabilidad de éxito. La variable p = P (S) y la variable\(q = P(F). q = 1 – p\).
- La variable aleatoria X puede tener valores de 0, 1, 2,... n.
La probabilidad se puede encontrar para cada número posible de éxitos que pueda tener la variable aleatoria X usando la fórmula de distribución binomial
\[P(X = x) = _nC_x P^x q^{n-x}\].
Si esta fórmula parece confusa, revisa el trabajo que hiciste al encontrar la probabilidad de que 3,5 o 6 personas crean que el dueño es responsable, porque en realidad estabas usando esta fórmula. \(_nC_x\), que se muestra en su calculadora como\(_nC_r\), es el número de combinaciones para x éxitos. La x y la r representan lo mismo y se usan indistintamente.
p es la probabilidad de éxito. Viene de la hipótesis nula.
q es la probabilidad de falla. Es el complemento de p.
n es el tamaño de la muestra
x es el número de éxitos
Si usamos esta fórmula para todos los valores posibles de la variable aleatoria, X, podemos crear la distribución binomial y la gráfica.
\(P(X = 0) = _6C_0(0.60)^0(0.40)^{6 - 0} = 0.0041\)
\(P(X = 1) = _6C_1(0.60)^1(0.40)^{6 - 1} = 0.0369\)
\(P(X = 2) = _6C_2(0.60)^2(0.40)^{6 - 2} = 0.1382\)Puedes terminar el resto de ellos.
La calculadora TI84 tiene una manera más fácil de crear esta distribución. Encuentra y presiona tu tecla Y=. El cursor debería aparecer en el espacio junto a Y1 =. A continuación, presione la\(2^{\text{nd}}\) llave, luego la llave con VARS en ella y DISTR.C/encima de ella. Esto te llevará a la colección de distribuciones. Desplázate hacia arriba hasta encontrar Binompdf. Esta es la función binomial de distribución de probabilidad. Selecciónala y luego ingresa los tres valores n, p, x. Por ejemplo, si ingresas Y1=Binompdf (6,0.60, x) y luego seleccionas\(2^{\text{nd}}\) TABLE, deberías ver una tabla que tenga el siguiente aspecto:
X Y1
0 0.0041
1 0.03686
2 0.13824
3 0.27648
4 0.31104
5 0.18662
6 0.04666
Si la tabla no se ve así, presione\(2^{\text{nd}}\) TBLSET y asegúrese de que su configuración sea:
TblStart = 0
\(\Delta\) TBL = 1
Indpnt: Auto
Depender: Auto.
Las distribuciones binomiales tienen media y desviación estándar. El enfoque para encontrar la media y desviación estándar de una distribución discreta se puede aplicar a una distribución binomial.
| \(X = x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(P(x = x)\) | 0.0041 | 0.0369 | 0.1382 | 0.2765 | 0.3110 | 0.1866 | 0.0467 |
| \(x(P(x))\) | 0 | 0.0369 | 0.2764 | 0.8295 | 1.244 | 0.933 | 0.2802 |
| \((x - \mu)^2\) | \((0 - 3.6)^2 = 12.96\) | 6.76 | 2.56 | 0.36 | 0.16 | 1.96 | 5.76 |
| \((x - \mu)^2 \cdot P(x)\) | 0.0531 | 0.2494 | 0.3538 | 0.0995 | 0.0498 | 0.3657 | 0.2690 |
\(\mu = \sum P(x) x\)
\(\mu = 0 + 0.0369+0.2764+0.8295+1.244+0.933+0.2802 = 3.6\)
\(\sigma = \sqrt{\sum[(x - \mu)^2 \cdot P(x)]}\)
\(\sigma = \sqrt{0.0531 + 0.2494 + 0.3538 + 0.0995 + 0.0498 + 0.3657 + 0.2690} = \sqrt{1.4403} = 1.20\)
La media también se llama el valor esperado de la distribución. Encontrar el valor esperado y la desviación estándar para usar estas fórmulas puede ser muy tedioso. Afortunadamente, para la distribución binomial, hay una manera más fácil. El valor esperado se puede encontrar con la fórmula:
\[E(x) = \mu = np\]
La desviación estándar se encuentra con la fórmula
\[\sigma = \sqrt{npq} = \sqrt{np(1 - p)}\]
Para determinar el número medio de personas que piensan que el propietario es responsable de los accidentes, utilice la fórmula
\(E(x) = \mu = np = 6\ (0.6) = 3.6\).
Esto indica que si se tomaran muchas muestras de 6 personas el promedio de personas que creen que el dueño es responsable sería de 3.6. Es aceptable que este promedio no sea un número entero.
La desviación estándar de esta distribución es:\(\sigma = \sqrt{np(1 - p)} = \sqrt{6 (0.6) (0.4)} = 1.2\)
Observe que los mismos resultados se obtuvieron con un proceso más fácil. Se deben utilizar las fórmulas 5.12 y 5.13 para encontrar la media y la desviación estándar para todas las distribuciones binomiales.
Aplicar este concepto de probabilidad a la hipótesis sobre la responsabilidad de un auto autónomo en un accidente.
Ahora que tienes la capacidad de crear una distribución binomial completa, estás listo para probar una hipótesis. Esto se demostrará con el ejemplo de automóvil autónomo que se ha utilizado a lo largo de este capítulo.
Supongamos que un investigador quería determinar la proporción de personas que creen que el dueño es responsable. El investigador pudo haber tenido la hipótesis de que la proporción de personas que creen que el propietario es responsable de los accidentes es superior al 60%. En este caso, las hipótesis serán: H0: p = 0.60 y H1: p > 0.60. El nivel de significancia será de 0.10 porque solo se utilizará un tamaño de muestra pequeño. En este caso, el tamaño de la muestra será de 6.
Con este tamaño de muestra ya hemos visto cómo será la distribución binomial. También sabemos que la dirección del extremo es hacia la derecha porque la hipótesis alternativa utiliza un símbolo mayor que.
El investigador selecciona aleatoriamente a 6 personas. De estos, cuatro dicen que el dueño es el responsable. ¿Qué hipótesis se sustenta en estos datos?
El valor p es la probabilidad de que el investigador obtenga cuatro o más personas alegando que el propietario es responsable. De la mesa que creamos antes, vemos la probabilidad de conseguir 4 personas que piensen
| \(X = x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| \(P(X = x)\) | 0.0041 | 0.0369 | 0.1382 | 0.2765 | 0.3110 | 0.1866 | 0.0467 |
el dueño es responsable es 0.3110, la probabilidad de obtener 5 es 0.1866 y la probabilidad de obtener 6 es 0.0467. Si sumamos estos juntos, encontramos que la probabilidad de obtener 4 o más es de 0.5443. Dado que esta probabilidad es mayor que nuestro nivel de significancia, concluimos que los datos apoyan la hipótesis nula y, por lo tanto, no son significativos. La conclusión que se escribiría es: En el nivel de significancia 0.10, la proporción de personas que piensan que el dueño es responsable no es significativamente mayor a 0.60 (\(x = 4\),\(p = 0.5443\),\(n = 6\)). Recuerde que en las conclusiones estadísticas, la p es el valor p, no la proporción muestral.
El TI84 tiene una manera rápida de sumar las probabilidades. Utiliza la función binomcdf, para la función binomial de distribución acumulativa. Se encuentra en la\(2^{\text{nd}}\) lista de distribuciones DISTR.COM. Binomcdf sumará todas las probabilidades comenzando por la izquierda, así binomcdf (6, .6,1) sumará las probabilidades para 0 y 1. Hay dos condiciones que se encuentran al probar hipótesis utilizando la distribución binomial. La manera de encontrar el valor p usando binomcdf se basa en la hipótesis alternativa.
Condición 1. La hipótesis alternativa tiene un signo menor que (<).
Dado que la dirección del extremo es hacia la izquierda, entonces usando binomcdf (n, p, x) producirá el valor p. La variable n representa el tamaño de la muestra, la variable p representa la probabilidad de éxito (ver hipótesis nula) y x representa el número específico de éxitos a partir de los datos.
Condición 2. La hipótesis alternativa tiene un signo mayor que (>).
Dado que la dirección del extremo es hacia la derecha, es necesario usar la regla del complemento y también reducir el valor de\(x\) en 1, así que ingrese 1 — binomcdf (\(n\),\(p\),\(x - 1\)) en su calculadora. Por ejemplo, si los datos son 4, entonces ingrese 1 — binomcdf (6,0.6,3). ¿Puedes averiguar por qué se usa x — 1 y por qué binomcdf (n, p, x-1) se resta de 1? Si no, pregunta en clase.
En este ejemplo, los datos no fueron significativos y por lo que el investigador no pudo afirmar que la proporción de personas que piensan que el dueño es responsable es mayor a 0.60. Un tamaño de muestra de 6 es muy pequeño para los datos categóricos y por lo tanto es difícil llegar a resultados significativos. Si se cambian los datos para que en lugar de sacar 4 de 6 personas, el investigador obtenga 400 de 600, ¿cambia la conclusión? Utilice 1 — binomcdf (600,0.6,399) para encontrar el valor p para esta situación.
1 — binomcdf (600,0.6,399) = ____________________
Escribe la frase final:
Paso 6 - ¿Cómo se puede encontrar el valor p aproximado usando la aproximación normal a la distribución binomial?
Cuando se prueba una hipótesis usando la distribución binomial, se encuentra un valor p exacto. Es exacto porque la distribución binomial se crea a partir de cada combinación de éxitos y fracasos que es posible para una muestra de tamaño n Existen otros métodos para determinar el valor p que darán un valor p aproximado. De hecho, el método típico que se utiliza para probar hipótesis sobre proporciones dará un valor p aproximado. Quizás te preguntes por qué se usa un método que da un valor p aproximado en lugar del método que da un valor p exacto. Esto se explicará una vez que se hayan demostrado los dos siguientes métodos. Antes de que estos puedan demostrarse, necesitamos aprender sobre una distribución diferente llamada distribución normal.
Digresión 6 — La distribución normal
Detrás de Pierce College se encuentra Waughop Lake, que es utilizado por muchos estudiantes para aprender conceptos científicos fuera de un aula. A continuación se muestra la forma aproximada del lago. Si uno de los laboratorios de ciencias requiriera que los estudiantes estimaran la superficie del agua, ¿qué estrategia podrían usar para este lago de forma irregular?
Una estrategia posible es pensar que este lago es casi un rectángulo, y así podrían dibujar un rectángulo sobre él. Ya que se conoce una fórmula para el área de un rectángulo, y si sabemos que cada flecha de abajo es de 200 metros, ¿se puede estimar el área del lago?
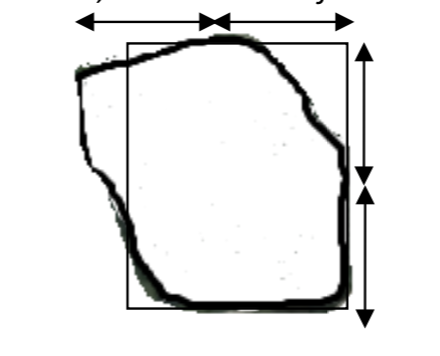
Hay dos preguntas importantes a considerar. Si se toma este enfoque, ¿el área del lago será exactamente igual al área del rectángulo? ¿Estará cerca?
La respuesta a la primera pregunta es no, a menos que pasara a ser extremadamente afortunados con nuestro dibujo del rectángulo. La respuesta a la segunda pregunta es sí debería estar cerca. 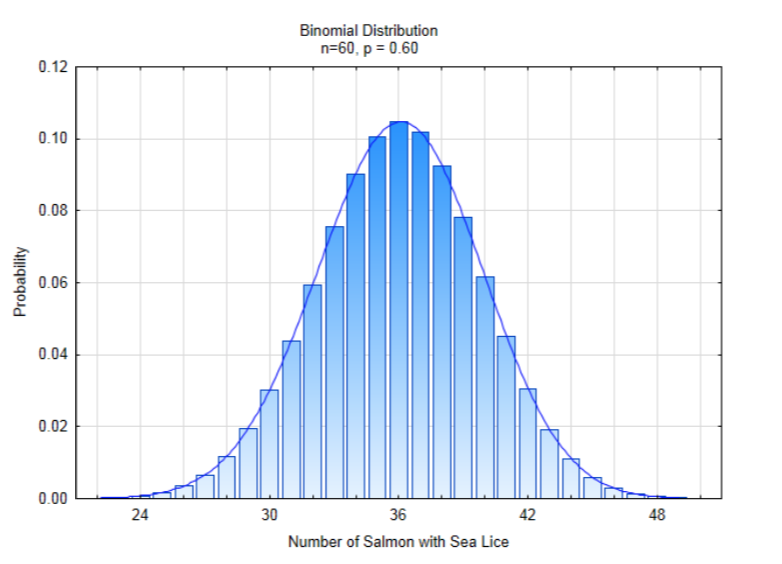
El concepto de aproximar una forma irregular con una forma para la que se conocen las propiedades es la estrategia que utilizaremos para encontrar nuevas formas de determinar un valor p. A la derecha está la forma irregular de una distribución binomial si n = 60, p = 0.60. La curva suave que se dibuja sobre la parte superior de las barras se llama distribución normal. También va por los nombres curva de campana y distribución gaussiana.
La fórmula para la distribución normal es\(f(x, \mu, \sigma) = \dfrac{1}{\sigma \sqrt{2\pi}} e^{[\dfrac{1}{2} (\dfrac{x - \mu}{\sigma})^2]}\). No es importante que conozcas esta fórmula. Lo importante es notar las variables que contiene. Ambos πy e son constantes con los valores de 3.14159 y 2.71828 respectivamente. La x es la variable independiente, la cual se encuentra a lo largo del eje x. Las variables importantes a notar son μ y σ, la media y la desviación estándar. La implicación de estas dos variables es que desempeñan un papel importante en la definición de esta curva. La función se puede mostrar como\(N(\mu,\sigma)\).
La distribución binomial es una distribución discreta mientras que la distribución normal es una distribución continua. Se le conoce como función de densidad.
Una distribución normal se contrasta con distribuciones sesgadas a continuación.
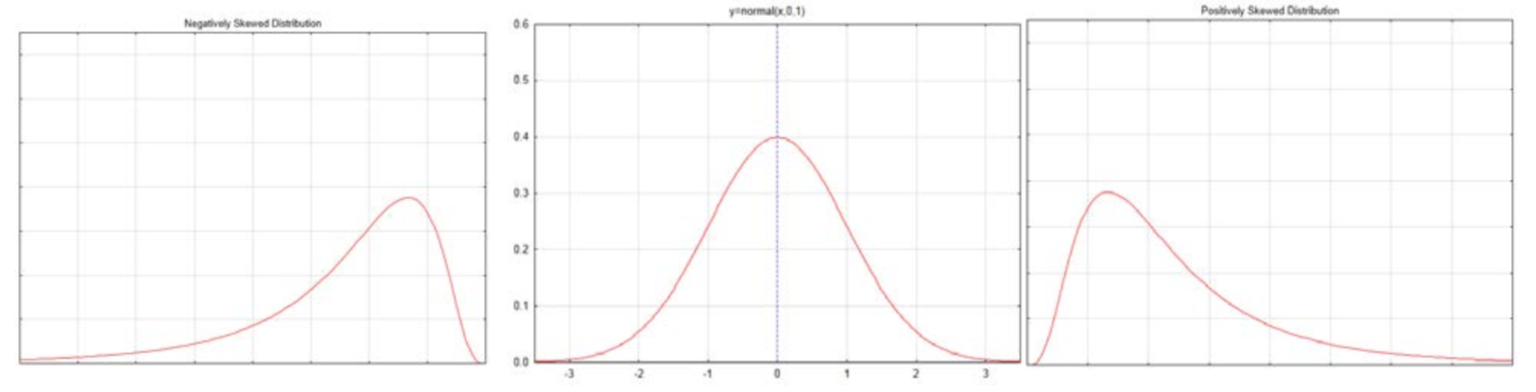
Una distribución sesgada negativamente, como la que se muestra a la izquierda, tiene algunos valores que son muy bajos haciendo que la curva se estire hacia la izquierda. Estos valores bajos harían que la media fuera menor que la mediana de la distribución. La distribución sesgada positivamente, como la que se muestra a la derecha, tiene algunos valores que son muy altos, provocando que la curva se estire hacia la derecha. Estos valores altos provocarían que la media fuera mayor que la mediana para la distribución. La curva normal en el medio es simétrica. La media, la mediana y el modo están todos en el medio. El modo es el punto alto de la curva.
La curva normal se denomina función de densidad, en contraste con la distribución binomial, que es una función de masa de probabilidad. El espacio bajo la curva se llama el área debajo de la curva. El área es sinónimo de probabilidad. El área bajo toda la curva, correspondiente a la probabilidad de seleccionar un valor de cualquier parte de la distribución es 1. Esta curva nunca toca el eje x, a pesar de que parece que lo hace. Nuestro objetivo final con la curva nor mal es encontrar el área en la cola, lo que corresponde con encontrar el valor p.
mal es encontrar el área en la cola, lo que corresponde con encontrar el valor p.
Empezaremos a pensar en el área (probabilidad) bajo la curva observando la curva normal estándar. La curva normal estándar tiene una media de 0 y una desviación estándar de 1 y se muestra como una función N (0,1). Observe que el eje x de la curva está numerado con —3, -2, -1, 0, 1, 2, 3. Estos números se llaman puntuaciones z. Representan el número de desviaciones estándar x es de la media, que se encuentra en el centro de la curva.
¿Parece razonable que la mitad de la curva esté a la izquierda de la media y la mitad la curva esté a la derecha? Podemos etiquetar cada lado con este valor, que se interpreta tanto como un área como una probabilidad de que exista un valor en esa área. 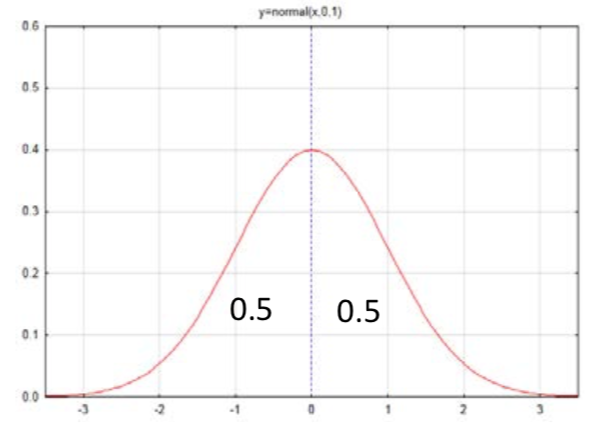
Pensar en el área bajo la distribución normal no es tan fácil como pensar en el área bajo una distribución uniforme. Por ejemplo, podríamos crear una distribución uniforme para el resultado de un experimento en el que se enrolla una matriz. La probabilidad de rodar cualquier número es 1/6. Por lo tanto, la distribución uniforme se vería así.
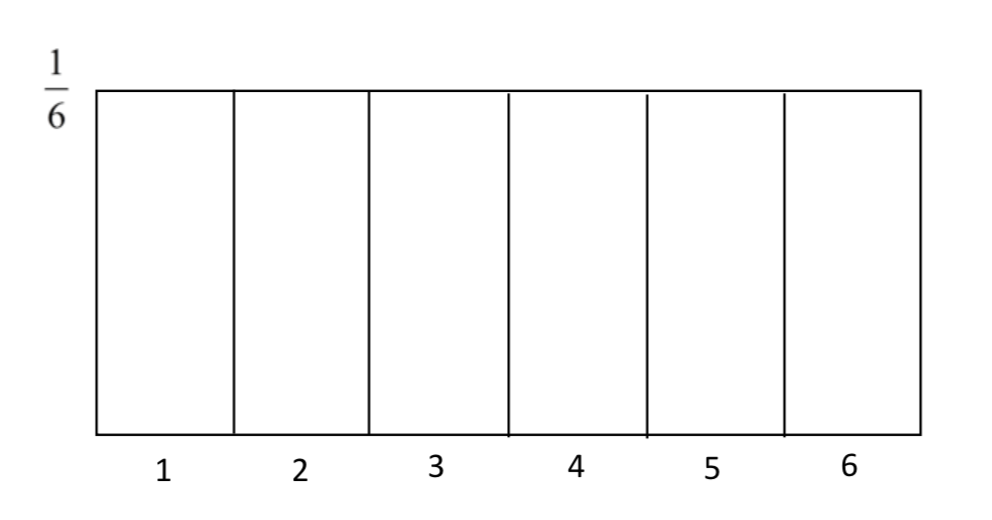
El área en esta distribución se puede encontrar multiplicando el largo por el ancho (alto). Así, para encontrar la probabilidad de obtener un 5 o superior, consideramos que la longitud es 2 y la anchura es 1/6 para que\(2 \times (\dfrac{1}{6} = \dfrac{1}{3}\). Es decir, hay una probabilidad de 1/3 de que un 5 o 6 se rodara en el dado.
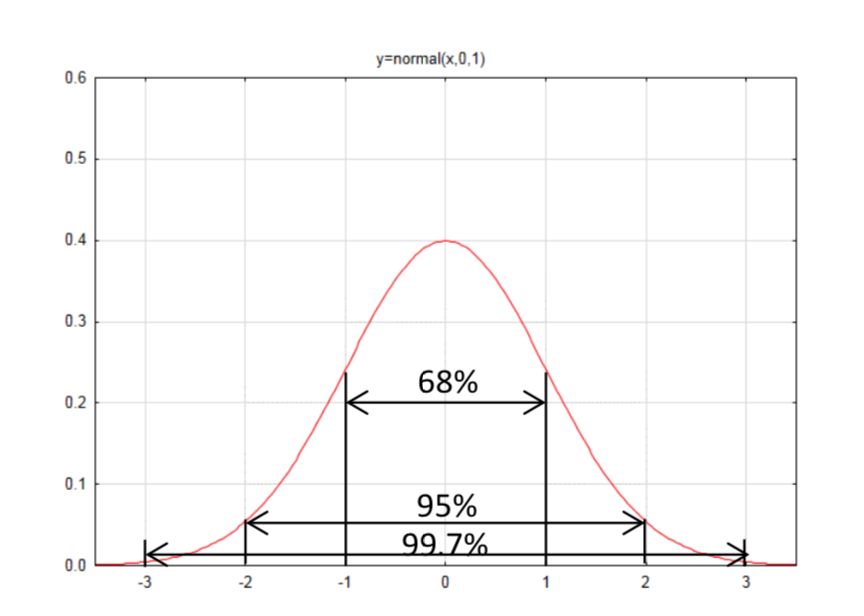
Pero una distribución normal no es tan familiar como un rectángulo, para lo cual el área es más fácil de encontrar. La Regla Empírica es una aproximación de las áreas para diferentes secciones de la curva normal; 68% de la curva está dentro de una desviación estándar de la media, 95% de la curva está dentro de dos desviaciones estándar de la media, y 99.7% de la curva está dentro de tres desviaciones estándar de la media.
Para encontrar el área bajo una distribución normal se realizó originalmente utilizando una técnica llamada integración, la cual se enseña en Cálculo. Sin embargo, estas áreas ya se han encontrado para la distribución normal estándar N (0,1) y se proporcionan en una tabla en la página siguiente. Las mesas siempre proporcionarán el área a la izquierda. El área a la derecha es el complemento del área a la izquierda, por lo que para encontrar el área a la derecha, restar el área a la izquierda de 1. Algunos ejemplos deberían ayudar a aclarar esto.
Ejemplo 3. Encuentra las áreas a la izquierda y derecha de z = -1.96.
Dado que el valor z es menor que 0, utilice la primera de las dos tablas. Encuentra la fila con — 1.9 en la columna izquierda y encuentra la columna con el 0.06 en la fila superior. La intersección de esas filas y columnas da el área a la izquierda, designada\(A_L\) como 0.0250. El área a la derecha, designada como\(A_R = 1 – 0.0250 = 0.9750\).
| Z | 0.09 | 0.08 | 0.07 | 0.06 | 0.05 | 0.04 | 0.03 | 0.02 | 0.01 | 0.00 |
| -1.9 | 0.0233 | 0.0239 | 0.0244 | 0.0250 | 0.0256 | 0.0262 | 0.0268 | 0.0274 | 0.0281 | 0.0287 |
Ejemplo 4. Encuentra las áreas a la izquierda y derecha de z = 0.57.
Dado que el valor z es mayor que 0, utilice la segunda de las dos tablas. Encuentra la fila con 0.5 en la columna izquierda y encuentra la columna con 0.07 en la fila superior. La intersección de esas filas y columnas da\(A_L = 0.7157\), por lo tanto\(A_R = 1 – 0.7157 = 0.2843\).
Distribución Normal Estándar — N (0,1)
Área a la izquierda cuando\(z \le 0\)
| Z | 0.09 | 0.08 | 0.07 | 0.06 | 0.05 | 0.04 | 0.03 | 0.02 | 0.01 | 0.00 |
| -3.5 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 |
| -3.4 | 0.0002 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 |
| -3.3 | 0.0003 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0005 | 0.0005 | 0.0005 |
| -3.2 | 0.0005 | 0.0005 | 0.0005 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | 0.0007 | 0.0007 |
| -3.1 | 0.0007 | 0.0007 | 0.0008 | 0.0008 | 0.0008 | 0.0008 | 0.0009 | 0.0009 | 0.0009 | 0.0010 |
| -3.0 | 0.0010 | 0.0010 | 0.0011 | 0.0011 | 0.0011 | 0.0012 | 0.0012 | 0.0013 | 0.0013 | 0.0013 |
| -2.9 | 0.0014 | 0.0014 | 0.0015 | 0.0015 | 0.0016 | 0.0016 | 0.0017 | 0.0018 | 0.0018 | 0.0019 |
| -2.8 | 0.0019 | 0.0020 | 0.0021 | 0.0021 | 0.0022 | 0.0023 | 0.0023 | 0.0024 | 0.0025 | 0.0026 |
| -2.7 | 0.0026 | 0.0027 | 0.0028 | 0.0029 | 0.0030 | 0.0031 | 0.0032 | 0.0033 | 0.0034 | 0.0035 |
| -2.6 | 0.0036 | 0.0037 | 0.0038 | 0.0039 | 0.0040 | 0.0041 | 0.0043 | 0.0044 | 0.0045 | 0.0047 |
| -2.5 | 0.0048 | 0.0049 | 0.0051 | 0.0052 | 0.0054 | 0.0055 | 0.0057 | 0.0059 | 0.0060 | 0.0062 |
| -2.4 | 0.0064 | 0.0066 | 0.0068 | 0.0069 | 0.0071 | 0.0073 | 0.0075 | 0.0078 | 0.0080 | 0.0082 |
| -2.3 | 0.0084 | 0.0087 | 0.0089 | 0.0091 | 0.0094 | 0.0096 | 0.0099 | 0.0102 | 0.0104 | 0.0107 |
| -2.2 | 0.0110 | 0.0113 | 0.0116 | 0.0119 | 0.0122 | 0.0125 | 0.0129 | 0.0132 | 0.0136 | 0.0139 |
| -2.1 | 0.0143 | 0.0146 | 0.0150 | 0.0154 | 0.0158 | 0.0162 | 0.0166 | 0.0170 | 0.0174 | 0.0179 |
| -2.0 | 0.0183 | 0.0188 | 0.0192 | 0.0197 | 0.0202 | 0.0207 | 0.0212 | 0.0217 | 0.0222 | 0.0228 |
| -1.9 | 0.0233 | 0.0239 | 0.0244 | 0.0250 | 0.0256 | 0.0262 | 0.0268 | 0.0274 | 0.0281 | 0.0287 |
| -1.8 | 0.0294 | 0.0301 | 0.0307 | 0.0314 | 0.0322 | 0.0329 | 0.0336 | 0.0344 | 0.0351 | 0.0359 |
| -1.7 | 0.0367 | 0.0375 | 0.0384 | 0.0392 | 0.0401 | 0.0409 | 0.0418 | 0.0427 | 0.0436 | 0.0446 |
| -1.6 | 0.0455 | 0.0465 | 0.0475 | 0.0485 | 0.0495 | 0.0505 | 0.0516 | 0.0526 | 0.0537 | 0.0446 |
| -1.5 | 0.0559 | 0.0571 | 0.0582 | 0.0594 | 0.0606 | 0.0618 | 0.0630 | 0.0643 | 0.0655 | 0.0668 |
| -1.4 | 0.0681 | 0.0694 | 0.0708 | 0.0721 | 0.0735 | 0.0749 | 0.0764 | 0.0778 | 0.0793 | 0.0808 |
| -1.3 | 0.0823 | 0.0838 | 0.0853 | 0.0869 | 0.0885 | 0.0901 | 0.0918 | 0.0934 | 0.0951 | 0.0968 |
| -1.2 | 0.0985 | 0.1003 | 0.1020 | 0.1038 | 0.1056 | 0.1075 | 0.1093 | 0.1112 | 0.1131 | 0.1151 |
| -1.1 | 0.1170 | 0.1190 | 0.1210 | 0.1230 | 0.1251 | 0.1271 | 0.1292 | 0.1314 | 0.1334 | 0.1357 |
| -1.0 | 0.1379 | 0.1401 | 0.1423 | 0.1446 | 0.1469 | 0.1492 | 0.1515 | 0.1539 | 0.1562 | 0.1587 |
| -0.9 | 0.1611 | 0.1635 | 0.1660 | 0.1685 | 0.1711 | 0.1736 | 0.1762 | 0.1788 | 0.1814 | 0.1841 |
| -0.8 | 0.1867 | 0.1894 | 0.1922 | 0.1949 | 0.1977 | 0.2005 | 0.2033 | 0.2061 | 0.2090 | 0.2119 |
| -0.7 | 0.2148 | 0.2177 | 0.2206 | 0.2236 | 0.2266 | 0.2296 | 0.2327 | 0.2358 | 0.2389 | 0.2420 |
| -0.6 | 0.2451 | 0.2483 | 0.2514 | 0.2546 | 0.2578 | 0.2611 | 0.2643 | 0.2676 | 0.2709 | 0.2743 |
| -0.5 | 0.2776 | 0.2810 | 0.2843 | 0.2877 | 0.2912 | 0.2946 | 0.2981 | 0.3015 | 0.3050 | 0.3085 |
| -0.4 | 0.3121 | 0.3156 | 0.3192 | 0.3228 | 0.3264 | 0.3300 | 0.3336 | 0.3372 | 0.3409 | 0.3446 |
| -0.3 | 0.3483 | 0.3520 | 0.2557 | 0.3594 | 0.3632 | 0.3669 | 0.3707 | 0.3745 | 0.3783 | 0.3821 |
| -0.2 | 0.4247 | 0.4286 | 0.4325 | 0.4364 | 0.4404 | 0.4443 | 0.4483 | 0.4522 | 0.4562 | 0.4602 |
| 0.0 | 0.4641 | 0.4681 | 0.4721 | 0.4761 | 0.4801 | 0.4840 | 0.4880 | 0.4920 | 0.4960 | 0.5000 |
Distribución Normal Estándar — N (0,1)
Área a la izquierda cuando\(z \ge 0\)
| Z | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.7190 | 0.7224 |
| 0.6 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7 | 0.7580 | 0.7611 | 0.7642 | 0.7673 | 0.7704 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1.0 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.8980 | 0.8997 | 0.9015 |
| 1.3 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0.9115 | 0.9131 | 0.9147 | 0.9162 | 0.9177 |
| 1.4 | 0.9192 | 0.9207 | 0.9222 | 0.9236 | 0.9251 | 0.9265 | 0.9279 | 0.9292 | 0.9306 | 0.9319 |
| 1.5 | 0.9332 | 0.9345 | 0.9357 | 0.9370 | 0.9382 | 0.9394 | 0.9406 | 0.9418 | 0.9429 | 0.9441 |
| 1.6 | 0.9452 | 0.9463 | 0.9474 | 0.9484 | 0.9495 | 0.9505 | 0.9515 | 0.9525 | 0.9535 | 0.9545 |
| 1.7 | 0.9554 | 0.9564 | 0.9573 | 0.9582 | 0.9591 | 0.9599 | 0.9608 | 0.9616 | 0.9625 | 0.9633 |
| 1.8 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.9699 | 0.9706 |
| 1.9 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.9750 | 0.9756 | 0.9761 | 0.9767 |
| 2.0 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
| 2.1 | 0.9821 | 0.9826 | 0.9830 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.9850 | 0.9854 | 0.9857 |
| 2.2 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9875 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.9890 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4 | 0.9918 | 0.9920 | 0.9922 | 0.9925 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
| 2.5 | 0.9938 | 0.9940 | 0.9941 | 0.9943 | 0.9945 | 0.9946 | 0.9948 | 0.9949 | 0.9951 | 0.9952 |
| 2.6 | 0.9953 | 0.9955 | 0.9956 | 0.9957 | 0.9959 | 0.9960 | 0.9961 | 0.9962 | 0.9963 | 0.9964 |
| 2.7 | 0.9965 | 0.9966 | 0.9967 | 0.9968 | 0.9969 | 0.9970 | 0.9971 | 0.9972 | 0.9973 | 0.9974 |
| 2.8 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.9980 | 0.9981 |
| 2.9 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
| 3.0 | 0.9987 | 0.9987 | 0.9987 | 0.9988 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9990 | 0.9990 |
| 3.1 | 0.9990 | 0.9991 | 0.9991 | 0.9991 | 0.9992 | 0.9992 | 0.9992 | 0.9992 | 0.9993 | 0.9993 |
| 3.2 | 0.9993 | 0.9993 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9995 | 0.9995 | 0.9995 |
| 3.3 | 0.9995 | 0.9995 | 0.. 9995 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 |
| 3.4 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9998 |
Dado que es muy poco probable que nos encontremos con poblaciones auténticas que normalmente se distribuyen con una media de cero y una desviación estándar de uno, entonces, ¿de qué sirve esto? La respuesta a esta pregunta tiene dos partes. La primera parte consiste en responder a la pregunta sobre qué poblaciones útiles se distribuyen normalmente. La segunda parte consiste en determinar cómo estas tablas pueden ser utilizadas por otras distribuciones con diferentes medias y desviaciones estándar.
Ya has visto que la curva normal encaja muy bien sobre la distribución binomial. En los capítulos uno y dos también se vieron distribuciones de proporciones muestrales y medias muestrales que se ven normalmente distribuidas. Por lo tanto, el uso primario de la distribución normal es encontrar probabilidades cuando se utiliza para modelar otras distribuciones como la distribución binomial o las distribuciones de muestreo de\(\hat{p}\) o\(\bar{x}\). A continuación se ilustran los elementos de las distribuciones modelados por la curva.
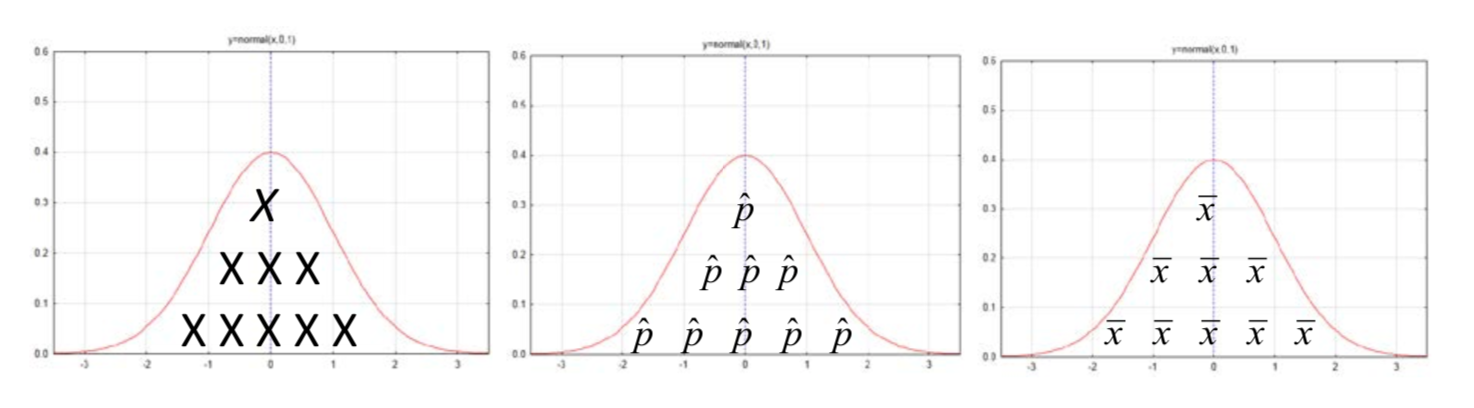
Ahora que se han establecido algunas de las distribuciones que se pueden modelar con una curva normal, podemos abordar la segunda pregunta, que es cómo hacer uso de las tablas para la curva normal estándar. Las probabilidades y más específicamente los valores p, solo se pueden encontrar después de que tengamos los resultados de nuestra muestra. Esos resultados de la muestra son parte de una distribución de posibles resultados que se distribuyen aproximadamente de manera normal. Al determinar el número de desviaciones estándar nuestros resultados de muestra son de la media de la población, podemos usar las tablas de distribución normal estándar para encontrar el valor p. La transformación de los resultados de la muestra en desviaciones estándar de la media hace uso de la fórmula z.
La puntuación z es el número de desviaciones estándar que un valor es de la media. Al restar el valor de la media y dividirlo por la desviación estándar, calculamos el número de desviaciones estándar. La fórmula es
\[z = \dfrac{x - \mu}{\sigma}\]
Esta es la fórmula básica sobre la que se construirán muchos otros.
Ejemplo 5
Supongamos que el número medio de éxitos en una muestra de 100 es 20 y la desviación estándar es 4. Esboza y etiqueta una curva normal y encuentra el área en la cola izquierda para el número 13. 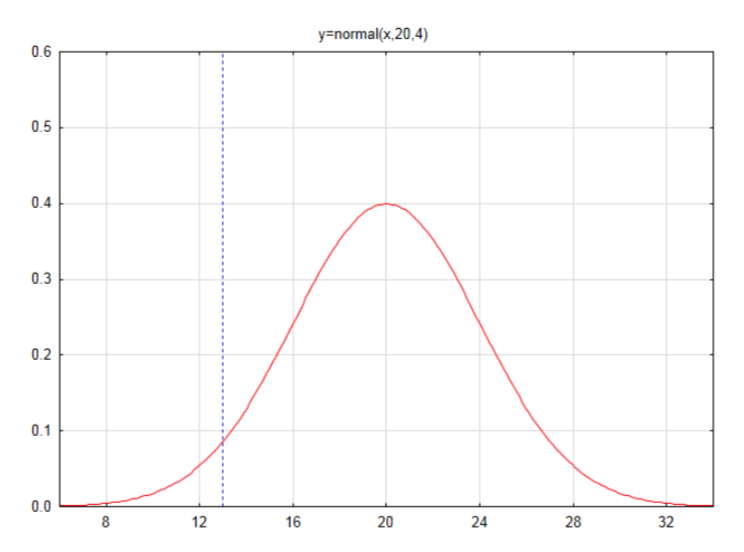
Primero encuentra la puntuación z:\(z = \dfrac{x - \mu}{\sigma}\)
\(z = \dfrac{13 - 20}{4} = -1.75\)
Encuentra el área a la izquierda en la tabla
\(A_L = 0.0401\)
Ejemplo 6
Si la media es 30 y la desviación estándar es 5, entonces dibuje y etiquete una curva normal y encuentre el área en la cola derecha para el número 44.1.
Primero encuentra la puntuación z:\(z = \dfrac{x - \mu}{\sigma}\)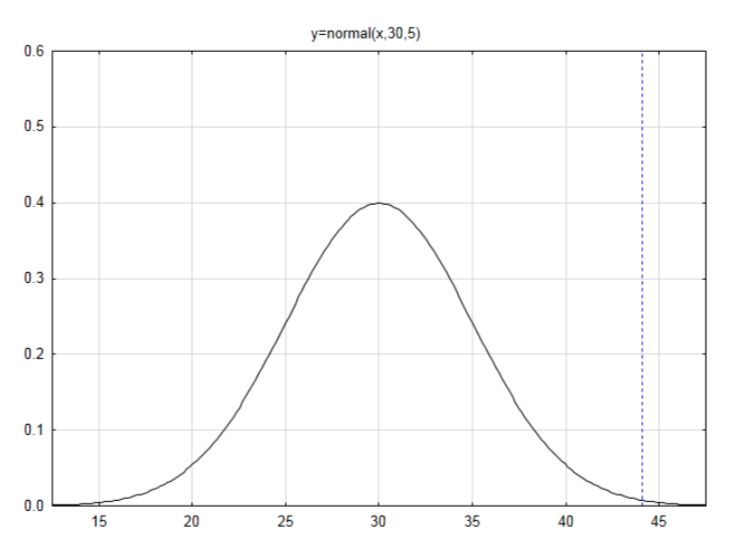
\(z = \dfrac{44.1 - 30}{5} = 2.82\)
Encuentra el área a la izquierda en la tabla
\(A_L = 0.9976\)
Use esto para encontrar el área a la derecha restando de 1.
\(A_R = 0.0024\)
Volver al Paso 6: Aplicar este concepto de probabilidad a la hipótesis sobre la responsabilidad de un auto autónomo en un accidente.
Recuerde que las hipótesis para el problema del automóvil autónomo son:\(H_0: p = 0.60\),\(H_1: p > 0.60\). En el problema original, el investigador encontró que 4 de cada 6 personas pensaban que el dueño era el responsable. ¿Qué hipótesis sustentan estos datos si el nivel de significancia es 0.10?
Esta prueba de hipótesis se realizará utilizando un método denominado Aproximación Normal a la Distribución Binomial.
El primer paso es encontrar la media y desviación estándar de la distribución binomial (que se hizo antes pero ahora se repite):
\(\mu = np = 6(0.6) = 3.6\)
\(\sigma = \sqrt{npq} = \sqrt{6(0.6)(0.4)} = 1.2\)
Dibujar y etiquetar una curva normal con una media de 3.6 y una desviación estándar de 1.2.
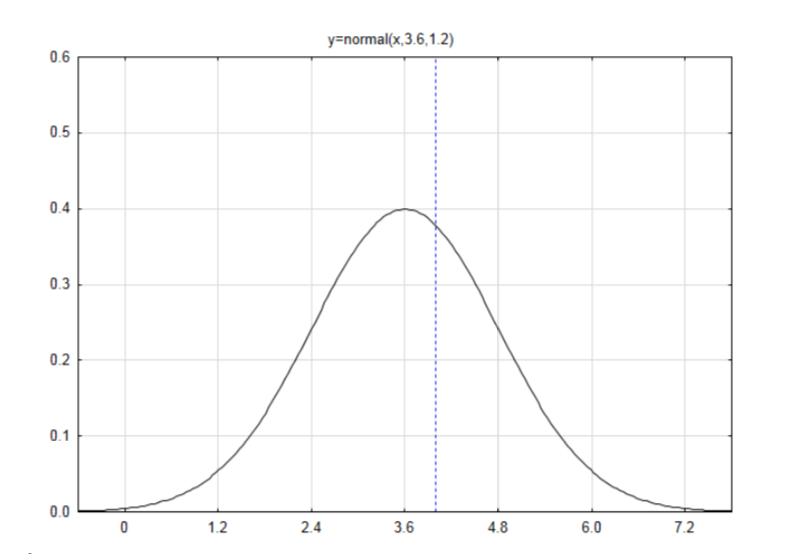
Encuentra la puntuación z si los datos son 4.
\(z = \dfrac{x - \mu}{\sigma}\)\(z = \dfrac{4 - 3.6}{1.2} = 0.33\)
De la mesa, el área a la izquierda es\(A_L = 0.6255\). Dado que la dirección del extremo es a la derecha, restar el área a la izquierda de 1 para llegar\(A_R = 0.3745\). Este es el valor p.
Este valor p también se puede encontrar con la calculadora (\(2^{\text{nd}}\)Distr #2: normalcdf (bajo, alto,\(\mu\),\(\sigma\))) que se muestra como normalcdf (4, 1E99, 3.6,1.2) =0.3694.
Dado que este valor es mayor que el nivel de significancia, si se usa el valor p generado por la calculadora, la conclusión se escribirá como: Al nivel de significancia 0.10, la proporción de personas que piensan que el dueño es responsable no es significativamente mayor a 0.60 (z = 0.33, p = 0.3694, n = 6).
Tomemos ahora un momento para comparar el valor p de la Aproximación Normal a la Distribución Binomial (0.3694) con el valor p exacto encontrado usando la Distribución Binomial (0.5443). Si bien estos p- valores no están muy próximos entre sí, la conclusión que se extrae es la misma. La razón por la que no están muy cerca es porque un tamaño de muestra de 6 es muy pequeño y la aproximación normal no es muy buena con un tamaño de muestra pequeño.
Vuelva a probar la hipótesis si el investigador encuentra que 400 de cada 600 personas creen que el dueño es responsable de los accidentes.
\(\mu = np = 600(0.6) = 360\)Esto indica que si se muestrearan muchas muestras de 600 personas el promedio de personas que piensan que el dueño es responsable sería de 360.
\(\sigma = \sqrt{npq} = \sqrt{600(0.6)(0.4)} = 12\)
Dibuja una etiqueta una curva con una media de 360 y una desviación estándar de 12.
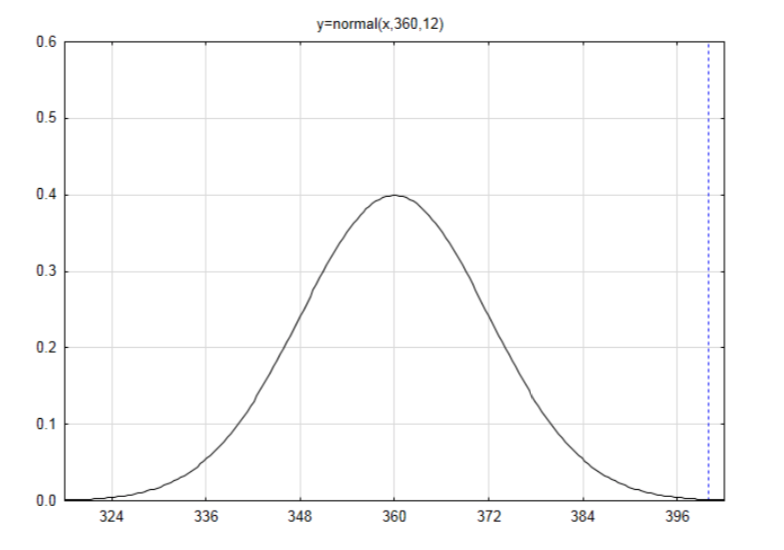
Encuentra la puntuación z si los datos son 400.
\(z = \dfrac{x - \mu}{\sigma}\)\(z = \dfrac{400 - 360}{12} = 3.33\)
Usando la tabla, el área a la izquierda es\(A_L = 0.9996\). Dado que la dirección del extremo es a la derecha, restar el área a la izquierda de 1 para llegar\(A_R = 0.0004\). Más precisamente, es 0.000430.
Esta vez cuando se comparan los resultados de la Aproximación Normal a la Distribución Binomial (0.000430) con los resultados de la distribución binomial (0.000443), son muy cercanos. Esto se debe a que el tamaño de la muestra es mayor.
En general, si\(np \ge 5\) y\(nq \ge 5\), entonces la aproximación normal hace una estimación buena, pero no perfecta para la distribución binomial. Cuando se utilizó una muestra de tamaño 6, la\(np = 3.6\) cual es menor a 5. También,\(nq = 6(0.4) = 2.4\), que es menos de 5, también. Por lo tanto, usar la aproximación normal para muestras que son pequeñas no es una buena estrategia.
Paso 7 — Encuentre el valor p aproximado usando la Distribución de Muestreo de Proporciones de Muestra
Hasta este punto la discusión ha sido sobre el número de personas. Cuando se realiza un muestreo que produce datos categóricos, estos números o recuentos también se pueden representar como proporciones dividiendo el número de éxitos por el tamaño de la muestra. Así, en lugar de que el investigador diga que 4 de cada 6 personas creen que el dueño es el responsable, el investigador podría decir que 66.7% de la gente cree que el dueño es responsable. Esto lleva al concepto de mirar las proporciones más que los recuentos lo que significa que en lugar de que la distribución esté conformada por el número de éxitos, representado por x, se compone de la proporción muestral de éxitos representados por \(\hat{p}\).
Digresión 7 — Distribución de Muestreo de Proporciones de Muestra
Dado que la distribución binomial contiene todos los recuentos posibles del número de éxitos y se distribuye aproximadamente normalmente y dado que todos los recuentos se pueden convertir a proporciones dividiendo por el tamaño de la muestra, entonces la distribución de también\(\hat{p}\) se distribuye aproximadamente normalmente. Esta distribución tiene una media y desviación estándar que se pueden encontrar dividiendo la media y desviación estándar de la distribución binomial por el tamaño muestral n.
La media de todas las proporciones muestrales es el número medio de éxitos dividido por n.
\(\mu_{\hat{p}} = \dfrac{\mu}{n} = \dfrac{np}{n} = p\)Esto indica que la media de todas las proporciones de muestra posibles es igual a la verdadera proporción para la población.
\[\mu_{\hat{p}} = p\]
La desviación estándar de todas las proporciones muestrales es la desviación estándar del número de éxitos dividido por n.
\(\sigma_{\hat{p}} = \dfrac{\sigma}{n} = \sqrt{\dfrac{npq}{n^2}} = \sqrt{\dfrac{pq}{n}}\ or\ \sqrt{\dfrac{p(1- p)}{n}}\)
\[\sigma_{\hat{p}} = \sqrt{\dfrac{pq}{n}}\ \ \ \ or \ \ \ \ \sigma_{\hat{p}} = \sqrt{\dfrac{p(1- p)}{n}}\]
La fórmula z básica ahora se\(z = \dfrac{x − \mu}{\sigma}\) puede reescribir sabiendo que en una distribución de proporciones muestrales, los resultados de la muestra que anteriormente se han representado con ahora se\(X\) pueden representar con\(\hat{p}\). La media, ahora se\(\mu\) puede representar con\(p\), ya\(\mu_{\hat{p}} = p\) y la desviación estándar ahora se\(\sigma\) puede representar con\(\sqrt{\dfrac{p(1- p)}{n}}\) since\(\sigma_{\hat{p}} = \sqrt{\dfrac{p(1- p)}{n}}\). Por lo tanto, para la distribución muestral de proporciones muestrales, la fórmula z\(z = \dfrac{x − \mu}{\sigma}\) se convierte en
\[z = \dfrac{\hat{p} - p}{\sqrt{\dfrac{p(1-p)}{n}}}.\]
Aplicar este concepto de probabilidad a la hipótesis sobre la responsabilidad de un auto autónomo en un accidente.
Recuerda que las hipótesis para las personas que piensan que el dueño es responsable son:\(H_0: p = 0.60\),\(H_1: p > 0.60\). En el problema original, el investigador encontró que 4 de cada 6 personas piensan que el dueño es el responsable. ¿Qué hipótesis sustentan estos datos si el nivel de significancia es 0.10?
Desde\(\mu_{\hat{p}} = p\) entonces la media es 0.60 (a partir de la hipótesis nula). 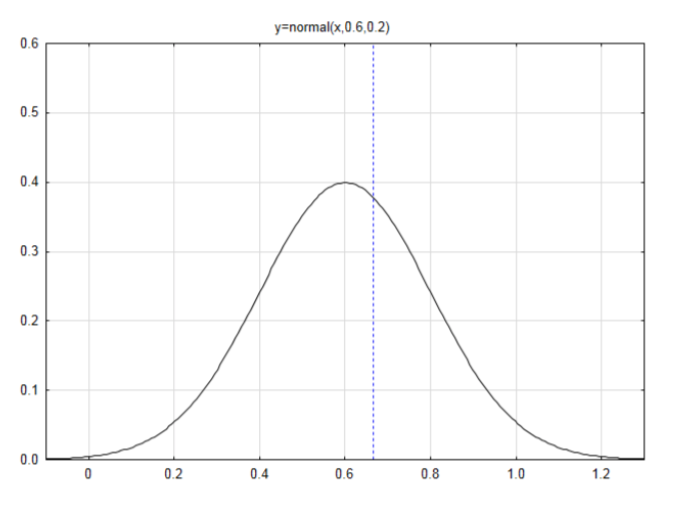
Desde\(\sigma_{\hat{p}} = \sqrt{\dfrac{p(1-p)}{n}} = \sqrt{\dfrac{0.6(0.4)}{6}} = 0.2\) entonces la desviación estándar es 0.2.
Dibuja una etiqueta una curva normal con una media de 0.6 y una
desviación estándar de 0.2.
Si los datos son 4, entonces la proporción de la muestra,
\(\hat{p} = \dfrac{x}{n} = \dfrac{4}{6} = 0.6667\)
Encuentra la puntuación z si los datos son 4.
\(z = \dfrac{\hat{p} - p}{\sqrt{\dfrac{p(1-p)}{n}}}\)\(z = \dfrac{0.6667 - 0.6}{0.2} = 0.33\)
El área a la izquierda es\(A_L = 0.6304\). Dado que la dirección del extremo es a la derecha, restar el área a la izquierda de 1 para llegar\(A_R = 0.3696\).
Compare este resultado con el resultado encontrado al usar la Aproximación Normal a la Distribución Binomial. Observe que ambos resultados son exactamente los mismos. Esto debería suceder cada vez, siempre que no haya ningún redondeo de números. La razón por la que esto ha sucedido es porque el número de éxitos se puede representar como recuentos o proporciones. Las distribuciones son las mismas, aunque el eje x está etiquetado de manera diferente. Divida las puntuaciones z para la aproximación normal por el tamaño de muestra 6 y obtendrá las puntuaciones z para la distribución muestral.
Vuelva a probar la hipótesis si el investigador encuentra que 400 de cada 600 personas creen que el dueño es el responsable.
Desde\(\mu_{\hat{p}} = p\) entonces la media es 0.60 (a partir de la hipótesis nula).
Desde\(\sigma_{\hat{p}} = \sqrt{\dfrac{p(1-p)}{n}} = \sqrt{\dfrac{0.6(0.4)}{600}} = 0.02\) entonces la desviación estándar es de 0.02.
Si los datos son 400, entonces la proporción de la muestra,\(\hat{p} = \dfrac{x}{n} = \dfrac{400}{600} = 0.66667\)
\(z = \dfrac{\hat{p} - p}{\sqrt{\dfrac{p(1-p)}{n}}}\)\(z = \dfrac{0.66667 - 0.6}{0.02} = 3.33\)
El área a la izquierda es\(A_L = 0.9996\). Dado que la dirección del extremo es a la derecha, restar el área a la izquierda de 1 para llegar\(A_R = 0.0004\). Más precisamente, es 0.000430.
Conclusión para probar hipótesis sobre datos categóricos.
En este momento, muchos estudiantes se preguntan por qué hay tres métodos y por qué el método de distribución binomial no es el único que se usa ya que produce un valor p exacto. Una justificación del uso del último método es comparar los resultados de encuestas u otros datos. Imagínese si una organización de noticias reportara sus resultados de una encuesta ya que 670 de 1020 estaban a favor mientras que otra organización informó que encontraron 630 de 980 estaban a favor. Una comparación entre estos sería difícil sin convertirlos a proporciones, por lo tanto, el tercer método, que utiliza proporciones, es el método de elección. Cuando el tamaño de la muestra es suficientemente grande, no hay mucha diferencia entre los métodos. Para muestras más pequeñas, puede ser más apropiado usar la distribución binomial.
Hacer inferencias utilizando datos cuantitativos
La estrategia para hacer inferencias con datos cuantitativos utiliza distribuciones de muestreo de la misma manera que se utilizaron para hacer inferencias sobre proporciones. En ese caso, se utilizó la distribución normal para modelar la distribución de las proporciones muestrales, p. Con datos cuantitativos, encontramos la media, por lo que se utilizará la distribución normal para modelar la distribución de medias muestrales, x.
Para demostrarlo, se utilizará una población pequeña. Esta población está conformada por los 50 estados de Estados Unidos más el Distrito de Columbia y los 5 territorios de Estados Unidos de Samoa Americana, Guam, Islas Marianas del Norte, Puerto Rico y las Islas Vírgenes, cada uno de los cuales cuenta con un representante en el Congreso con limitada autoridad electoral. Se proporciona un histograma que muestra la distribución del número de representantes en un estado o territorio. En la gráfica se encuentra una distribución normal basada en la media de esta población siendo 7.875 representantes y una desviación estándar de 9.487. La distribución está sesgada positivamente y no puede ser modelada por la curva normal que está en la gráfica.
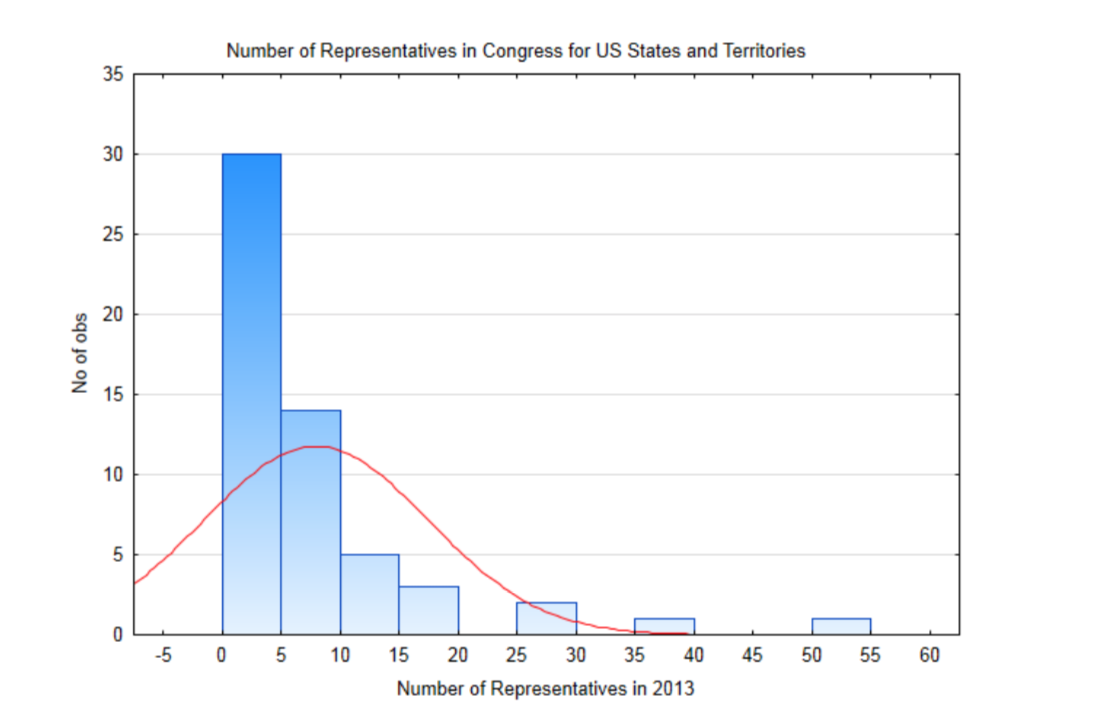
Tenga en cuenta que en realidad, la media y la desviación estándar, que son parámetros, no se conocen y así normalmente escribiríamos hipótesis sobre ellos. Sin embargo, para esta demostración, es necesaria una población pequeña con una media conocida y desviación estándar. Con esto, es posible ilustrar lo que sucede cuando se extraen muestras repetidas del mismo tamaño de esta población, con reemplazo, y se encuentran las medias de cada muestra y se convierten en parte de la distribución de medias muestrales.
Una distribución muestral de medias muestrales (una distribución de x) contiene todas las medias muestrales posibles que en teoría podrían obtenerse si se utilizara un proceso de selección aleatoria, con reemplazo. El número de posibles medias muestrales se puede encontrar utilizando la regla fundamental del conteo. Dibuja una línea para representar cada estado/territorio que se seleccionaría. En la línea escribe el número de opciones, para que se vea así:
| Opciones: | 56 | 56 | 56 | 56 | 56 |
| Estado: | 1 | 2 | 3 | 4... | n |
Si nuestro tamaño de muestra es 40, entonces hay\(56^{40}\) posibles muestras que podrían ser seleccionadas que es igual a\(8.46 \times 10^{69}\). Eso es un montón de muestras posibles. Para esta demostración, solo se tomarán 10,000 muestras de tamaño 40. La distribución de estas medias de muestra cuando se hizo esto se muestra en el histograma a continuación.
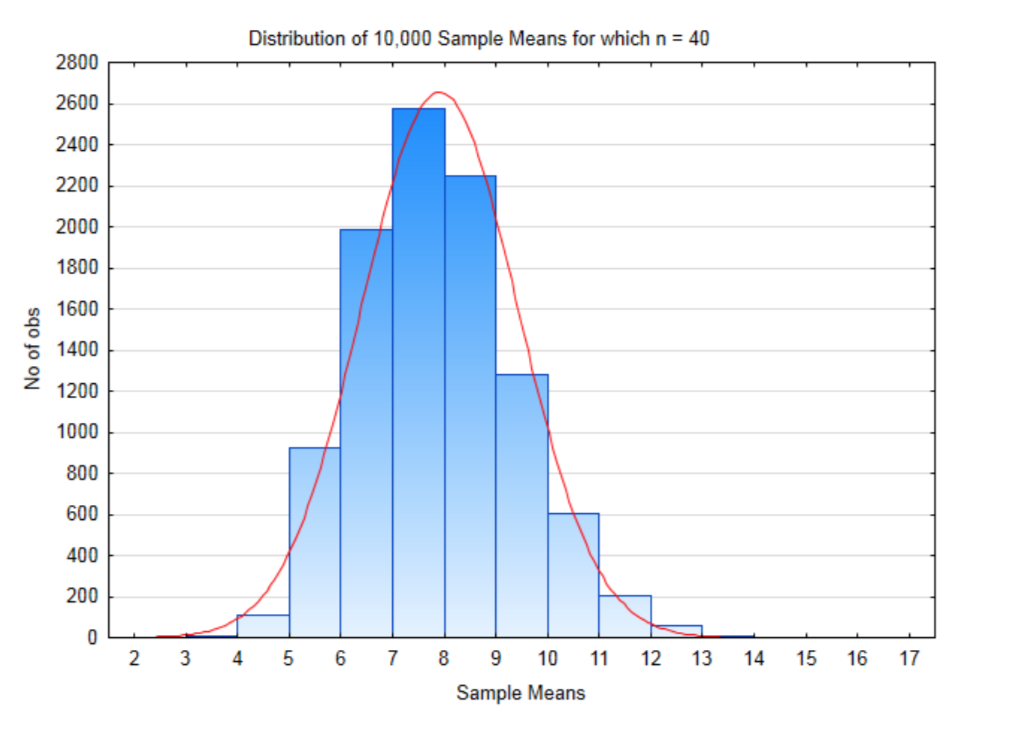
La media de todas estas medias muestrales es 7.8748 y la desviación estándar es 1.502. Observe que la media de todas estas medias muestrales es casi exactamente la misma que la media de la población original. También observe que la desviación estándar de todas estas medias muestrales es mucho menor que la desviación estándar de la población. Esto se resume en la siguiente tabla.
| Población | Distribución de Muestreo | |
|---|---|---|
| Media | 7.875 | 7.8748 |
| Desviación estándar | 9.487 | 1.502 |
La siguiente gráfica tiene tanto los datos originales como las medias de la muestra en ella. Observe cómo las dos curvas normales están centradas aproximadamente en el mismo lugar pero la curva para las medias de la muestra es más estrecha. Esto demuestra que cuando se toman muestras de tamaño suficiente de cualquier población, las medias de esas muestras estarán cerca de las medias de la población.
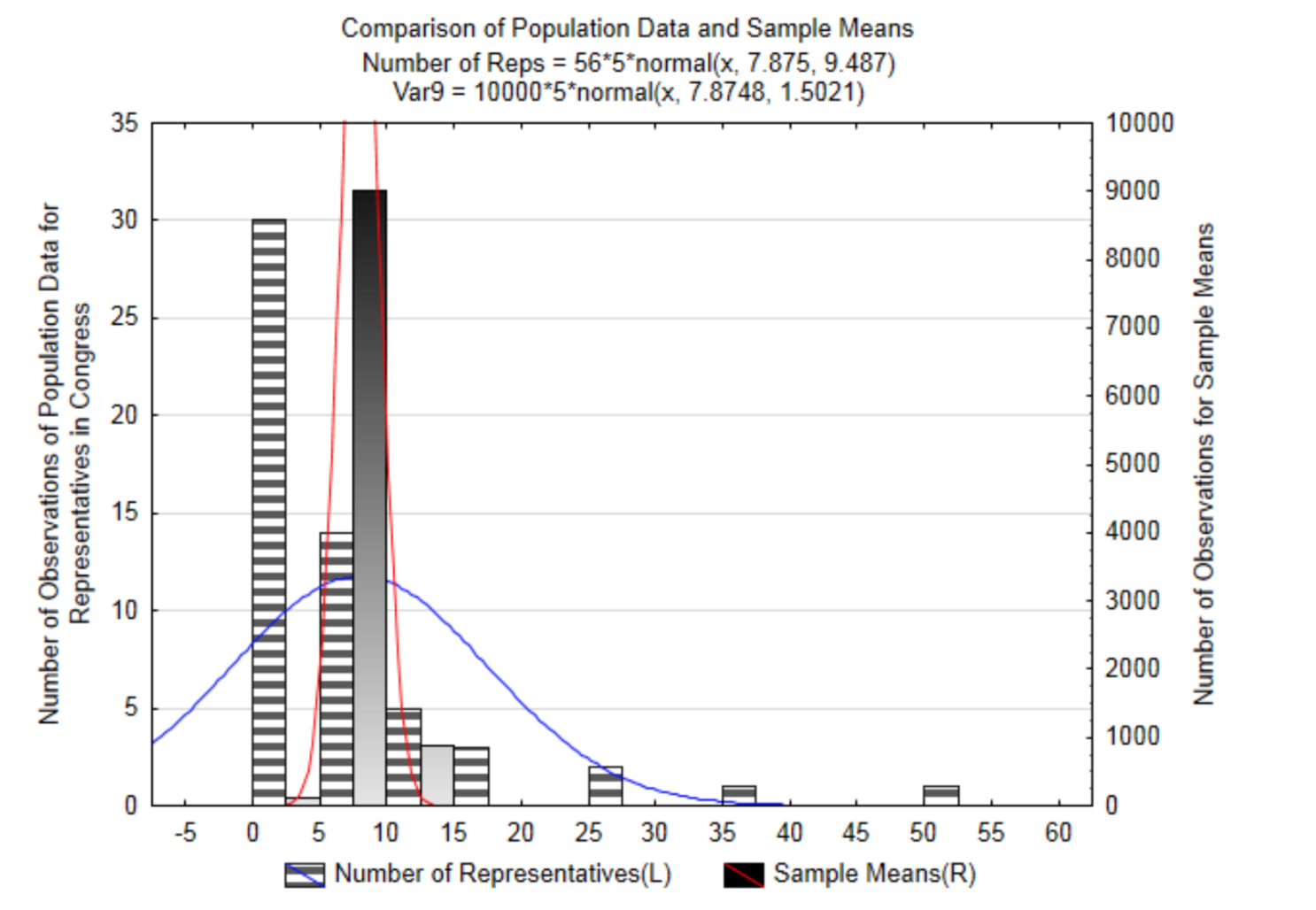
Ya estamos listos para discutir el Teorema del Límite Central. Este teorema establece que para cualquier conjunto de datos cuantitativos con una media μ y una desviación estándar σ, la media de todas las medias muestrales posibles será igual a la media de la población. La desviación estándar de todas las medias muestrales, que también se denomina error estándar, será igual a la desviación estándar de la población dividida por la raíz cuadrada de n, que se muestran como:
\[\mu_{\bar{x}} = \mu\]
y
\[\sigma_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}}.\]
También dice que la distribución de las medias muestrales será normal si el tamaño de la muestra es suficientemente grande (generalmente se considera 30 o más). Si la población original se distribuye normalmente, entonces la distribución de las medias muestrales se distribuirá normalmente para cualquier tamaño de muestra.
Antes de hacer un ejemplo, será importante ver el efecto de los tamaños de muestra. Compare las siguientes 4 gráficas que muestran la distribución de medias de muestra para muestras de tamaño 40, 30, 20 y 10.
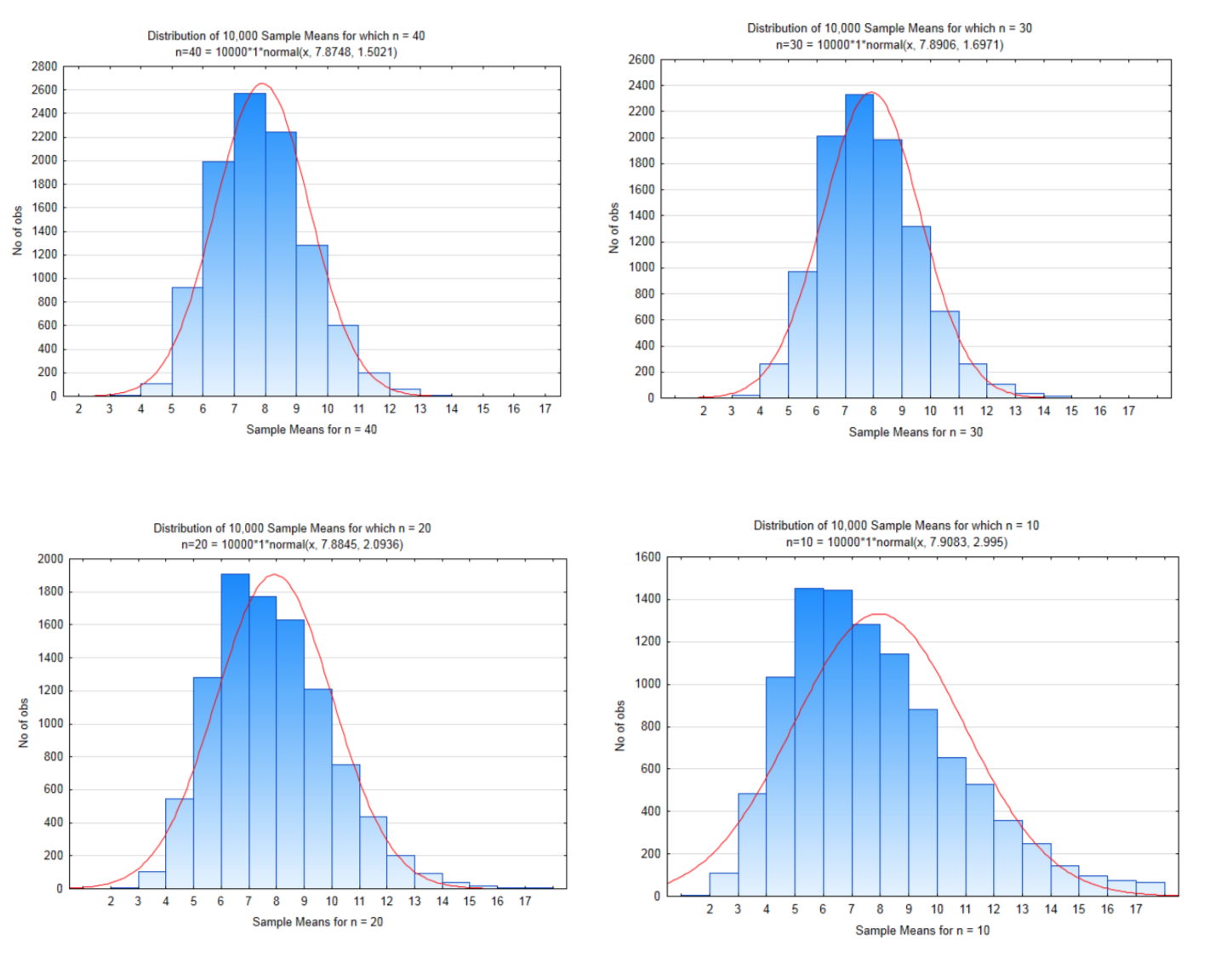
Observe cómo las distribuciones se vuelven más sesgadas a medida que disminuye el tamaño de la muestra. Observe también que la media de las medias de la muestra sigue siendo aproximadamente igual a la media de la población pero las desviaciones estándar se hacen mayores a medida que el tamaño de la muestra se hace más pequeño. Esto implica que hay más variación en las medias de muestra con tamaños de muestra pequeños que con tamaños de muestra grandes.
| Población | \(n = 40\) | \(n = 30\) | \(n = 20\) | \(n = 10\) | |
|---|---|---|---|---|---|
| Media | 7.875 | \ (n = 40\)” style="vertical-align:middle; ">7.8748 | \ (n = 30\)” style="vertical-align:middle; ">7.8906 | \ (n = 20\)” style="vertical-align:middle; ">7.8845 | \ (n = 10\)” style="vertical-align:middle; ">7.9083 |
| Desviación estándar | 9.487 | \ (n = 40\)” style="vertical-align:middle; ">1.5021 | \ (n = 30\)” style="vertical-align:middle; ">1.6971 | \ (n = 20\)” style="vertical-align:middle; ">2.0936 | \ (n = 10\)” style="vertical-align:middle; ">2.995 |
| Desviación estándar calculada usando \(\sigma_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}}\) |
\ (n = 40\)” style="vertical-align:middle; ">1.500 | \ (n = 30\)” style="vertical-align:middle; ">1.732 | \ (n = 20\)” style="vertical-align:middle; ">2.121 | \ (n = 10\)” style="vertical-align:middle; ">3.000 |
Al hacer inferencias sobre datos cuantitativos, la\(z\) fórmula básica ahora se\(z = \dfrac{x − μ}{\sigma}\) puede reescribir sabiendo que en una distribución de medias muestrales, los resultados de la muestra con la que anteriormente se han representado ahora se\(x\) pueden representar con\(\bar{x}\). La media, todavía se\(\mu\) representará con\(\mu\), ya que\(\mu_{\bar{x}} = \mu\) y la desviación estándar ahora se\(\sigma\) puede representar con\(\dfrac{\sigma}{\sqrt{n}}\) desde\(\sigma_{\bar{x}} = \dfrac{\sigma}{\sqrt{n}}\)
Por lo tanto, para la distribución muestral de medias muestrales, la\(z\) fórmula,\(z = \dfrac{x − μ}{\sigma}\) se convierte en
\[z = \dfrac{\bar{x} - \mu}{\dfrac{\sigma}{\sqrt{n}}}.\]
Ahora es el momento de utilizar el teorema del límite central para probar una hipótesis.
Ejemplo 7
Ejemplo 7 El mercurio en los peces no es saludable y se ponen restricciones en la cantidad de pescado que se debe comer. Supongamos que un investigador quisiera saber si la concentración promedio de metilmercurio por kilogramo de tejido de pescado fue mayor al límite máximo recomendado de 300 μg/kg. Si la concentración promedio es mayor a 300, se cerrarán las pesquerías, de lo contrario permanecerán abiertas. Supongamos también que la desviación estándar para la población es\(\sigma = 50 \mu g/kg\). El investigador captura 36 peces. La concentración media de la muestra es 310.
Las hipótesis a probar son:
\(H_0: \mu = 300\)
\(H_1: \mu > 300\)
\(\alpha = 0.1\)
Dado que toda la información que se necesita se proporciona en el problema, el primer paso es encontrar la\(z\) puntuación.
\(z = \dfrac{\bar{x} - \mu}{\dfrac{\sigma}{\sqrt{n}}} = \dfrac{310 - 300}{\dfrac{50}{\sqrt{36}}} = 1.2.\)
El siguiente paso es buscar 1.20 en las tablas de distribución normal estándar. Esto da un área a la izquierda de\(A_L=0.8849\) y así el área a la derecha está\(A_R = 0.1151\). Este es un valor p.
Dado que el valor p es mayor que el nivel de significancia, la conclusión es que la concentración promedio de metilmercurio en el tejido de peces no es significativamente mayor a 300\(\mu\) g/kg (\(z\)= 1.20,\(p\) = 0.1151,\(n\) = 36). Por lo tanto, las pesquerías no se cerrarán a la pesca
Ejemplo 8
Según una estimación, el tiempo promedio de espera para viviendas subsidiadas para personas sin hogar es de 35 meses. (www.stcloudstate.edu/reslife/... Statistics.pdf visto 9/13/13) Supongamos que la distribución de los tiempos es normal y la desviación estándar es de 10 meses. Una ciudad evalúa su programa actual y para ver si es efectivo y justifica el financiamiento continuado. Si el tiempo promedio de espera es menor a 35 meses, el programa continuará. De lo contrario, el programa será reemplazado por otro programa diferente.
Las hipótesis a probar son:
- \(H_0: \mu = 35\)
- \(H-1: \mu < 35\)
\(\alpha = 0.01\)
A continuación se registra el tiempo de espera (en meses) de veinte personas que recientemente recibieron vivienda subsidiada.
| 44 | 23 | 26 | 27 | 22 | 33 | 20 | 28 | 8 | 22 |
| 23 | 19 | 12 | 23 | 12 | 7 | 17 | 4 | 18 | 33 |
Ya que se nos dan los datos, debemos encontrar la media de la muestra antes de encontrar la puntuación z.
\(\bar{x} = 21.05\)
\(z = \dfrac{\bar{x} - \mu}{\dfrac{\sigma}{\sqrt{n}}} = \dfrac{21.05 - 35}{\dfrac{10}{\sqrt{20}}} = -6.24.\)
Debido a que la dirección del extremo es a la izquierda encontramos el área a la izquierda en la tabla de distribución normal estándar. La puntuación z más baja que encontramos en esa tabla es de -3.49. El área a la izquierda de -3.49 es 0.0002. Yendo aún más a la izquierda, el área será menor que eso. Por lo tanto, el valor p para estos datos es <0.0002. La cantidad de tiempo de espera antes de que las personas reciban vivienda subsidiada con el programa actual es significativamente menor a 35 meses (z = -6.24, p < 0.0002, n = 20). Con base en la regla de decisión, el programa es efectivo y continuará siendo financiado.


