Caso Q→Q
- Última actualización
- Guardar como PDF
- Page ID
- 151238
CO-4: Distinguir entre diferentes escalas de medición, elegir los métodos estadísticos descriptivos e inferenciales adecuados con base en estas distinciones e interpretar los resultados.
Objetivos de aprendizaje
LO 4.35: Para una situación de análisis de datos que involucre dos variables, elija el método inferencial apropiado para examinar la relación entre las variables y justificar la elección.
Objetivos de aprendizaje
LO 4.36: Para una situación de análisis de datos que involucre dos variables, llevar a cabo el método inferencial apropiado para examinar las relaciones entre las variables y sacar las conclusiones correctas en contexto.
CO-5: Determinar alternativas metodológicas preferidas a los métodos estadísticos de uso común cuando no se cumplen los supuestos.
Comentario: De UNIT 1
Video
Video: Caso Q→Q (60:27)
Tutoriales SAS relacionados
- 9A — (3:53) Gráficas de dispersión básicas
- 9B — (2:29) Gráficas de dispersión agrupadas
- 9C — (3:46) Coeficiente de correlación de Pearson
- 9D — (3:00) Regresión lineal simple — EDA
- 9E — (5:59) Regresión lineal simple (inferencia)
Tutoriales relacionados con SPSS
- 9A — (2:38) Gráficas de dispersión básicas
- 9B — (2:54) Gráficas de dispersión agrupadas
- 9C — (3:35) Coeficiente de correlación de Pearson
- 9D — (2:53) Regresión lineal simple — EDA
- 9E — (7:07) Regresión lineal simple (inferencia)
Introducción
En inferencia para las relaciones, hasta el momento hemos aprendido procedimientos de inferencia para ambos casos C→Q y C→C de la tabla de clasificación de rol/tipo a continuación.
El último caso a considerar en este curso es el caso Q→Q, donde tanto las variables explicativas como las de respuesta son cuantitativas. (El caso Q→C requiere métodos estadísticos que vayan más allá del alcance de este curso, uno de los cuales es la regresión logística).

Para el caso Q→Q, aprenderemos las siguientes pruebas:
| Muestras Dependientes | Muestras Independientes | |
|---|---|---|
| Prueba (s) estándar |
|
|
| Prueba (s) no paramétrica |
|
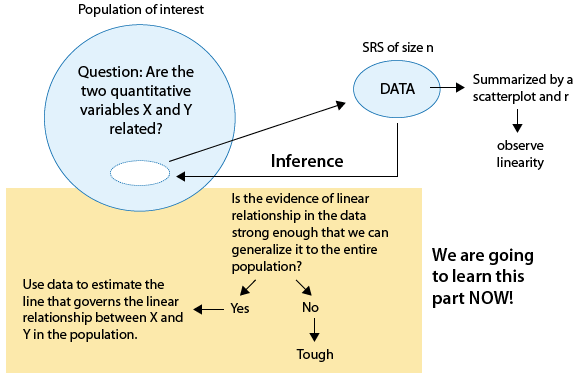
En la sección Análisis Exploratorio de Datos, se examinó la relación entre los valores de muestra para dos variables cuantitativas observando una gráfica de dispersión y si la relación era lineal, se complementó la gráfica de dispersión con el coeficiente de correlación r y la ecuación de regresión lineal. Se discutió la ecuación de regresión pero no se intentó afirmar que la relación observada en la muestra necesariamente se mantuvo para la población más grande de la que se originó la muestra.
Ahora que tenemos una mejor comprensión del proceso de inferencia estadística, discutiremos algunos métodos para inferir algo sobre la relación entre dos variables cuantitativas en una población entera, a partir de la relación observada en la muestra.
En particular, nos centraremos en las relaciones lineales y responderemos a las siguientes preguntas:
- ¿El coeficiente de correlación es diferente de cero en la población, o podría ser que obtuvimos el resultado en los datos sólo por casualidad?
- ¿La pendiente es diferente de cero en la población, o podría ser que obtuvimos el resultado en los datos sólo por casualidad?
Si satisfacemos los supuestos y condiciones para utilizar los métodos, podemos estimar la pendiente y el coeficiente de correlación para nuestra población y realizar pruebas de hipótesis sobre estos parámetros.
Para las pruebas estándar, las pruebas para la pendiente y el coeficiente de correlación son equivalentes; siempre producirán el mismo valor p y conclusión. Esto se debe a que están directamente relacionados entre sí.
En esta sección, podemos exponer nuestras hipótesis nulas y alternativas como:
Ho: No hay relación entre las dos variables cuantitativas X e Y.
Ha: Existe una relación entre las dos variables cuantitativas X e Y.
Coeficiente de correlación de Pearson
Objetivos de aprendizaje
LO 4.45: En un contexto dado, establecer las hipótesis nulas y alternativas apropiadas para examinar la relación entre dos variables cuantitativas.
Objetivos de aprendizaje
LO 4.46: En un contexto dado, determinar el método estándar apropiado para examinar la relación entre dos variables cuantitativas interpretar los resultados proporcionados en la salida del software apropiado en contexto.
Lo que sabemos de la Unidad 1:
- r solo mide la asociación LINEAL entre dos variables cuantitativas X e Y
- -1 ≤ r ≤ 1
- Si la relación es lineal entonces:
r = 0 implica que no hay relación entre X e Y (¡tenga en cuenta que esta es nuestra hipótesis nula!!)
r > 0 implica una relación positiva entre X e Y (a medida que X aumenta, Y también aumenta)
r < 0 implica una relación negativa entre X e Y (a medida que X aumenta, Y disminuye)
Ahora aquí están los pasos para la prueba de hipótesis para el coeficiente de correlación de Pearson:
Paso 1: Indicar las hipótesis Si consideramos la información anterior y nuestra hipótesis nula,
Ho: No hay relación entre las dos variables cuantitativas X e Y,
Antes de que podamos escribir esto usando correlación, debemos definir el coeficiente de correlación poblacional. En estadística, utilizamos la letra griega ρ (rho) para denotar el coeficiente de correlación poblacional. Así, si no hay relación entre las dos variables cuantitativas X e Y en nuestra población, podemos ver que esta hipótesis es equivalente a
Ho: ρ = 0 (rho = 0).
La hipótesis alternativa será
Ha: ρ ≠ 0 (rho no es igual a cero).
sin embargo, son posibles pruebas unilaterales.
Paso 2: Obtener datos, verificar condiciones y resumir datos
(i) La muestra debe ser aleatoria con observaciones independientes (todas las observaciones son independientes de todas las demás observaciones).
(ii) La relación debe ser razonablemente lineal, lo cual podemos verificar usando un diagrama de dispersión. Cualquier relación claramente no lineal no debe analizarse utilizando este método.
(iii) Para realizar esta prueba, ambas variables deben distribuirse normalmente las cuales podemos verificar usando histogramas y gráficas QQ. Los valores atípicos pueden causar problemas.
Aunque existe un estadístico de prueba intermedio, en efecto, el valor de r en sí sirve como nuestro estadístico de prueba.
Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
Confiaremos en el software para obtener el valor p para esta prueba. Ya hemos visto este valor p cuando calculamos correlación en la Unidad 1.
Paso 4: Conclusión
Como es habitual, utilizamos la magnitud del valor p para sacar nuestras conclusiones. Un pequeño valor p indica que la evidencia proporcionada por los datos es lo suficientemente fuerte como para rechazar Ho y concluir (más allá de una duda razonable) que las dos variables están relacionadas (ρ ≠ 0). En particular, si se usa un nivel de significancia de 0.05, rechazaremos Ho si el valor p es menor que 0.05.
Se pueden obtener intervalos de confianza para estimar el verdadero coeficiente de correlación poblacional, ρ (rho), sin embargo, no vamos a computar estos intervalos en este curso. Se le podría pedir que interprete o use un intervalo de confianza que se le haya proporcionado.
Alternativa no paramétrica: correlación de rangos de Spearman
Objetivos de aprendizaje
LO 5.1: Para una situación de análisis de datos que involucre dos variables, determinar el método alternativo apropiado (no paramétrico) cuando no se cumplan los supuestos de nuestros métodos estándar.
Objetivos de aprendizaje
LO 5.2: Reconocer situaciones en las que la correlación de rangos de Spearman es una medida más apropiada de la relación entre dos variables cuantitativas
Veremos una prueba no paramétrica en el caso Q→Q. La correlación de rangos de Spearman utiliza los mismos cálculos que para el coeficiente de correlación de Pearson, excepto que usa los rangos en lugar de los datos originales. Esta prueba es útil cuando hay valores atípicos o cuando las variables no parecen estar distribuidas normalmente.
- Esta medida y prueba son más útiles cuando la relación entre X e Y es no lineal y ya sea no creciente o no decreciente.
- Si la relación tiene componentes crecientes y decrecientes, la correlación de rangos de Spearman no suele ser útil como medida de correlación.
Esta medida se comporta de manera similar a r en que:
- va de -1 a 1
- un valor de 0 implica que no hay relación
- los valores positivos implican una relación positiva
- los valores negativos implican una relación negativa.
Ahora un ejemplo:
EJEMPLO: IQ vs Cry
Un método para predecir el coeficiente intelectual tan pronto como sea posible después del nacimiento podría ser importante para la intervención temprana en casos como anomalías cerebrales o discapacidades de aprendizaje. Se ha pensado que una mayor vocalización infantil (por ejemplo, más llanto) se asocia con un coeficiente intelectual más alto. En 1964, se emprendió un estudio para ver si el coeficiente intelectual a los 3 años de edad se asocia con la cantidad de llanto a la edad del recién nacido. En el estudio, se hizo llorar a 38 recién nacidos después de ser tocados en el pie y se contó el número de vocalizaciones de llanto distintas en 20 segundos. Los sujetos fueron seguidos a los 3 años de edad y se midieron sus CI.
Datos: formato SPSS, formato SAS, formato Excel
Variable de respuesta:
- CI a los tres años de edad
Variable explicativa:
- Recuento de llanto recién nacido en 20 segundos
Resultados:
Paso 1: Exponer las hipótesis
Las hipótesis son:
Ho: No hay relación entre el recuento de llantos recién nacidos y el coeficiente intelectual a los tres años de edad
Ja: Existe una relación entre el recuento de llantos recién nacidos y el coeficiente intelectual a los tres años de edad
Pasos 2 y 3: Obtener datos, verificar condiciones, resumir datos y f ind el valor p
(i) A lo mejor de nuestro conocimiento las asignaturas son independientes.
(ii) La gráfica de dispersión muestra una relación razonablemente lineal aunque no muy fuerte.
(iii) Los histogramas y las gráficas QQ para ambas variables están ligeramente sesgados a la derecha. Preferiríamos distribuciones más simétricas; sin embargo, la asimetría no es extrema por lo que procederemos con cautela.
El coeficiente de correlación de Pearson es de 0.402 con un valor p de 0.012.
La correlación de rangos de Spearman es de 0.354 con un valor p de 0.029.
Paso 4: Conclusión
Con base en la gráfica de dispersión y los resultados de correlación, existe una correlación positiva estadísticamente significativa, pero algo débil, entre el recuento de llantos recién nacidos y el coeficiente intelectual a los 3 años.
Regresión lineal simple
Objetivos de aprendizaje
LO 4.46: En un contexto dado, determinar el método estándar apropiado para examinar la relación entre dos variables cuantitativas interpretar los resultados proporcionados en la salida del software apropiado en contexto.
En la Unidad 1 se discutió el método de mínimos cuadrados para estimar la línea de regresión y se utilizó software para obtener la pendiente e intercepción de la ecuación de regresión lineal. Estas estimaciones pueden considerarse como las estadísticas muestrales que estiman la verdadera pendiente e interceptación de la población.
Ahora formalizaremos la regresión lineal simple que requerirá alguna notación adicional.
Un modelo de regresión expresa dos ingredientes esenciales:
- una tendencia de la variable de respuesta Y a variar con la variable explicativa X de manera sistemática (determinista)
- una dispersión estocástica de puntos alrededor de la curva de relación estadística (aleatoria)
La regresión es un vasto tema que maneja una amplia variedad de relaciones posibles.
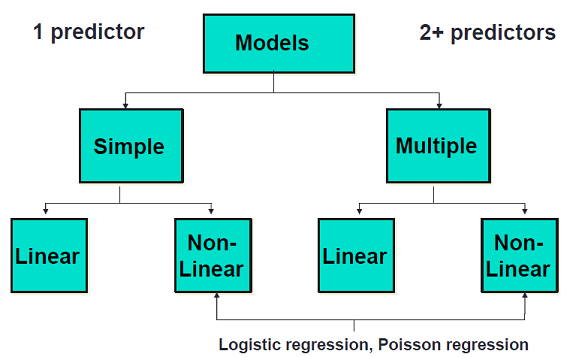
Todos los métodos de regresión comienzan con un modelo teórico que especifica la forma de la relación e incluye los supuestos o condiciones necesarios. Ahora introduciremos una definición más “estadística” del modelo de regresión y definiremos los parámetros en la población.
Modelo de Regresión Lineal Simple:
Aquí usaremos una notación diferente a la del inicio del semestre. Ahora usamos la notación de estilo de modelo de regresión.
Suponemos que la relación en la población es lineal y por lo tanto nuestro modelo de regresión puede escribirse como:
\(Y_i = \beta_0 + \beta_1 X_i + \epsilon_i\)
donde
- El parámetro β 0 (beta_cero) es la intercepción (en la población) y es el valor promedio de Y cuando X = 0
- El parámetro β 1 (beta_1) es la pendiente (en la población) y es el cambio en la Y promedio por cada 1 unidad de incremento en X.
- X i es el valor de la variable explicativa para la i-ésima asignatura
- Y i es el valor de la variable de respuesta para el i-ésimo sujeto
- ε i (epsilon_i) es el término de error para el tema i-ésimo
- se supone que los términos de error son
- normalmente distribuido con cero medio (verificar con histograma y gráfica QQ de los residuos)
- varianza constante (verificación con diagrama de dispersión de Y vs. X para regresión lineal simple)
- estadísticamente independiente (difícil de verificar, asegúrese de tener observaciones independientes en los datos, ¡se requieren diferentes métodos para las observaciones dependientes!)
La siguiente imagen ilustra los componentes de este modelo.
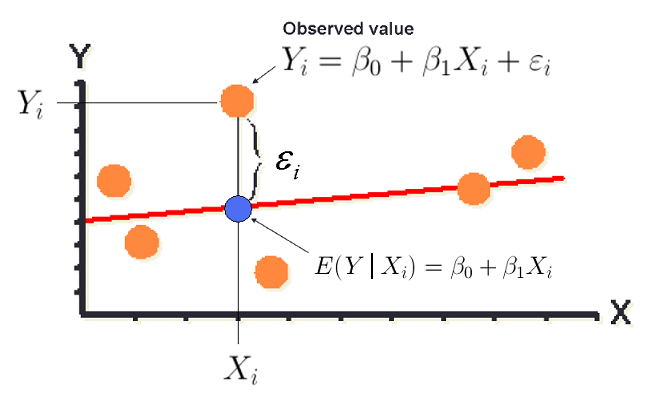
Cada punto naranja representa una observación individual en la gráfica de dispersión. Cada valor observado se modela usando la ecuación anterior.
\(Y_i = \beta_0 + \beta_1 X_i + \epsilon_i\)
La línea roja es la línea de regresión lineal verdadera. El punto azul representa el valor predicho para un valor X particular e ilustra que nuestro valor predicho solo estima la media, promedio o valor esperado de Y en ese valor X.
Se espera el error para un individuo y se debe a la variación en nuestros datos. En la ilustración anterior, está etiquetada con ε i (epsilon_i) y denotada por un corchete que da la distancia entre el punto naranja para el valor observado y el punto azul para el valor predicho para un valor particular de X. En la práctica, no podemos observar el verdadero error para un individuo pero nosotros podrá estimarlos usando los residuales, que pronto definiremos matemáticamente.
La línea de regresión representa la Y promedio para una X dada y se puede expresar como en símbolos como el valor esperado de Y para una X, E (Y|X) o Y-hat dada.
\(E(Y|X_i) = \hat{Y}_i = \hat{\beta}_0 + \hat{\beta}_1 X_i\)
En la Unidad 1, usamos a para representar la intercepción y b para representar la pendiente que estimamos a partir de nuestros datos.
En los procedimientos formales de regresión, comúnmente usamos beta para representar el parámetro poblacional y beta-hat para representar la estimación del parámetro.
Estas estimaciones de parámetros, que son estadísticas de muestra estimadas a partir de nuestros datos, también se denominan a veces los coeficientes usando terminología álgebra.
Para cada observación en nuestro conjunto de datos, también tenemos un residuo que se define como la diferencia entre el valor observado y el valor predicho para esa observación.
\(\text{residual}_i = Y_i - \hat{Y}_i\)
Los residuos se utilizan para verificar nuestros supuestos de normalidad y varianza constante.
En efecto, dado que tenemos una variable de respuesta cuantitativa, seguimos comparando medias poblacionales. No obstante, ahora debemos hacerlo por CADA valor posible de X. Queremos saber si la distribución de Y es la misma o diferente sobre nuestro rango de valores X.
Esta idea se ilustra (incluyendo nuestro supuesto de normalidad) en la siguiente imagen que muestra un caso donde la distribución de Y está cambiando a medida que cambian los valores de la variable explicativa X. Este cambio se ve reflejado solo por un cambio en las medias ya que asumimos normalidad y variación constante de Y para todos X.
El método utilizado es matemáticamente equivalente al ANOVA pero nuestras interpretaciones son diferentes debido a la naturaleza cuantitativa de nuestra variable explicativa.
Esta imagen muestra una gráfica de dispersión y una línea de regresión en el plano X-Y —como si estuvieran planas sobre una tabla. Luego de pie —en el eje vertical— dibujamos curvas normales centradas en la línea de regresión para cuatro valores X diferentes, con X aumentando para cada uno.
El centro de las distribuciones de las distribuciones normales que se muestran muestra un incremento en la media pero variación constante.
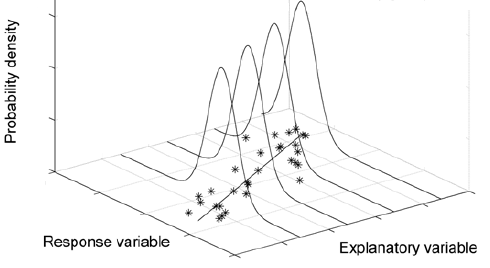
La idea es que el modelo asume que una distribución normal es una buena aproximación de cómo variarán los valores Y alrededor de la línea de regresión para un valor particular de X.
Coeficiente de Determinación
Objetivos de aprendizaje
LO 4.47: Para modelos de regresión lineal simple, interpretar el coeficiente de determinación en contexto.
Hay una medida adicional que suele ser de interés en la regresión lineal, el coeficiente de determinación, R2 que, para regresión lineal simple es simplemente el cuadrado del coeficiente de correlación, r.
El valor de R2 se interpreta como la proporción de variación en nuestra variable de respuesta Y, lo cual puede explicarse por el modelo de regresión lineal utilizando nuestra variable explicativa X.
Inmuebles Importantes de R 2
- 0 ≤ R 2 ≤ 1
- R 2 = 0 implica que el modelo no explica ninguna variación en Y.
- R 2 = 1 implica que el modelo explica toda la variación en Y (ajuste perfecto, muy poco probable con datos)
Un R 2 grande puede o NO significar que el modelo se ajuste bien a nuestros datos.
La siguiente imagen ilustra datos con un R 2 bastante grande pero el modelo no se ajusta bien a los datos.
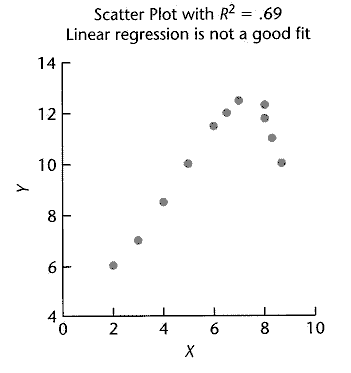
Un pequeño R 2 puede o PUEDE NO significar que no hay relación entre X e Y —debemos tener cuidado ya que la relación que existe puede simplemente no estar especificada en nuestro modelo— actualmente un modelo lineal simple.
La imagen de abajo ilustra datos con una R 2 muy pequeña pero la verdadera relación es muy fuerte.
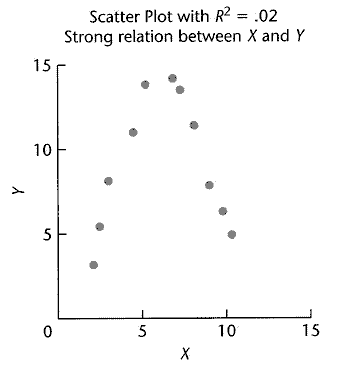
Procedimiento de Prueba para la Pendiente en Regresión Lineal Simple
Ahora nos movemos a nuestro procedimiento de prueba formal para regresión lineal simple.
Un R2 pequeño puede o NO puede significar que no hay relación entre X e Y —debemos tener cuidado ya que la relación que existe puede simplemente no estar especificada en nuestro modelo— actualmente un modelo lineal simple. La imagen de abajo ilustra datos con un R2 muy pequeño pero la verdadera relación es muy fuerte.
Paso 1: Exponer las hipótesis
Con el fin de poner a prueba la hipótesis de que
Ho: No hay relación entre las dos variables cuantitativas X e Y,
asumiendo que nuestro modelo es correcto (un modelo lineal es suficiente), podemos escribir la hipótesis anterior como
Ho: β 1 = 0 (Beta_1 = 0, la pendiente de nuestra ecuación lineal = 0 en la población).
La hipótesis alternativa será
Ha: β 1 ≠ 0 (Beta_1 no es igual a cero).
Paso 2: Obtener datos, verificar condiciones y resumir datos
(i) La muestra debe ser aleatoria con observaciones independientes (todas las observaciones son independientes de todas las demás observaciones).
(ii) La relación debe ser lineal que podemos verificar usando un diagrama de dispersión.
(iii) Los residuos deben estar razonablemente distribuidos normalmente con varianza constante que podemos verificar utilizando los métodos que se discuten a continuación.
Normalidad: Histograma y gráfica QQ de los residuos.
Varianza constante: Gráfica de dispersión de Y vs. X y/o una gráfica de dispersión de los residuos frente a los valores predichos (Y-hat). Nos gustaría ver dispersión aleatoria sin patrón y aproximadamente la misma dispersión para todos los valores de X.
Los grandes valores atípicos que caen fuera del patrón de los datos pueden causar problemas y ejercer una influencia indebida en nuestras estimaciones. Vimos en la Unidad 1 que una observación que está muy lejos en el eje x puede tener un gran impacto en los valores de correlación y pendiente.
Aquí hay dos ejemplos cada uno usando las dos parcelas mencionadas anteriormente.
Ejemplo 1: Tiene varianza constante (homocedasticidad)
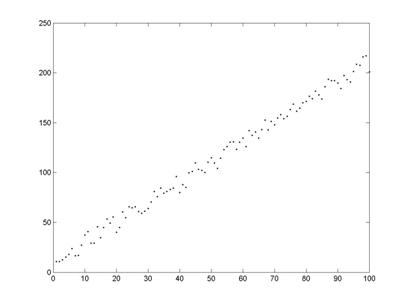
Gráfico de dispersión de Y vs. X (arriba)
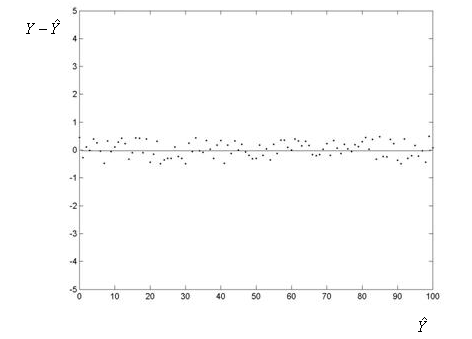
Gráfica de dispersión de los residuos frente a los valores predichos (arriba)
Ejemplo 2: No tiene varianza constante (heterocedasticidad)
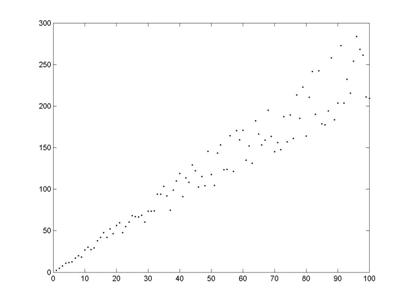
Gráfico de dispersión de Y vs. X (arriba)
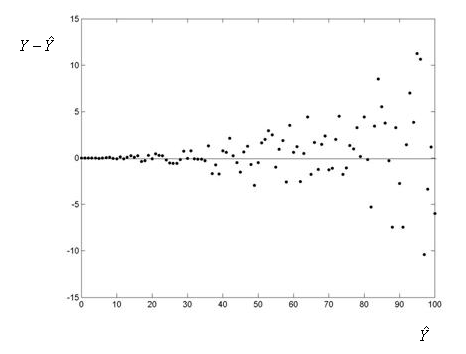
Gráfica de dispersión de los residuos frente a los valores predichos (arriba)
El estadístico de prueba es similar a los que hemos estudiado para otras pruebas t:
\(t = \dfrac{\hat{\beta}_1 - 0}{\text{SE}_{\hat{\beta}_1}}\)
donde
\(\text{SE}_{\hat{\beta}_1}\)= error estándar de\(\hat{\beta}_1\).
Ambos valores, junto con el estadístico de prueba, se proporcionan en la salida del software.
Paso 3: Encuentre el valor p de la prueba usando el estadístico de prueba de la siguiente manera
Bajo la hipótesis nula, el estadístico de prueba sigue una distribución t con n-2 grados de libertad. Confiaremos en el software para obtener el valor p para esta prueba.
Paso 4: Conclusión
Como es habitual, utilizamos la magnitud del valor p para sacar nuestras conclusiones. Un pequeño valor p indica que la evidencia proporcionada por los datos es lo suficientemente fuerte como para rechazar Ho y concluiríamos que hay suficiente evidencia de que la pendiente de sombrero en la población no es cero y por lo tanto las dos variables están relacionadas. En particular, si se usa un nivel de significancia de 0.05, rechazaremos Ho si el valor p es menor que 0.05.
También se obtendrán intervalos de confianza en el software para estimar la verdadera pendiente poblacional, β 1 (beta_1).
EJEMPLO: IQ vs Cry
Un método para predecir el coeficiente intelectual tan pronto como sea posible después del nacimiento podría ser importante para la intervención temprana en casos como anomalías cerebrales o discapacidades de aprendizaje. Se ha pensado que una mayor vocalización infantil (por ejemplo, más llanto) se asocia con un coeficiente intelectual más alto. En 1964, se emprendió un estudio para ver si el coeficiente intelectual a los 3 años de edad se asocia con la cantidad de llanto a la edad del recién nacido. En el estudio, se hizo llorar a 38 recién nacidos después de ser tocados en el pie y se contó el número de vocalizaciones de llanto distintas en 20 segundos. Los sujetos fueron seguidos a los 3 años de edad y se midió su coeficiente intelectual.
Datos: formato SPSS, formato SAS, formato Excel
Variable de respuesta:
- CI a los tres años de edad
Variable explicativa:
- Recuento de llanto recién nacido en 20 segundos
Resultados:
Paso 1: Exponer las hipótesis
Las hipótesis son:
Ho: No existe una relación (lineal) entre el recuento de llantos recién nacidos y el coeficiente intelectual a los tres años de edad
Ja: Existe una relación (lineal) entre el recuento de llantos recién nacidos y el coeficiente intelectual a los tres años de edad
Pasos 2 y 3: Obtener datos, verificar condiciones, resumir datos y f ind el valor p
(i) A lo mejor de nuestro conocimiento las asignaturas son independientes.
(ii) La gráfica de dispersión muestra una relación razonablemente lineal aunque no muy fuerte.
(iii) El histograma y la gráfica QQ de los residuos están ambos razonablemente distribuidos normalmente. Las gráficas de dispersión de Y vs. X y los residuales vs. los valores predichos no muestran evidencia de varianza no constante.
La ecuación de regresión estimada es
\(\hat{IQ} = 90.76 + 1.54 (\text{cry count})\)
El parámetro estimado de la pendiente es 1.54 lo que significa que por cada incremento de 1 unidad en el conteo de llanto, se espera que el coeficiente intelectual promedio aumente en 1.54 puntos.
El error estándar de la estimación de la pendiente es 0.584 que dan un estadístico de prueba de 2.63 en la salida y utilizando valores no redondeados de la salida y la fórmula:
\(t = \dfrac{\hat{\beta}_1 - 0}{\text{SE}_{\hat{\beta}_1}} = \dfrac{1.536 - 0}{0.584} = 2.63\).
Se encuentra que el valor p es 0.0124. Observe esto exactamente igual que obtuvimos para estos datos para nuestra prueba del coeficiente de correlación de Pearson. Estos dos métodos son equivalentes y siempre producirán la misma conclusión sobre la significancia estadística de la relación lineal entre X e Y.
El intervalo de confianza del 95% para β 1 (beta_1) dado en la salida es (0.353, 2.720).
Este modelo de regresión tiene un coeficiente de determinación de R2 = 0.161 lo que significa que 16.1% de la variación en el puntaje de CI a los tres años puede ser explicada por nuestro modelo de regresión lineal utilizando conteo de llantos recién nacidos. Esto confirma una relación relativamente débil como encontramos en nuestro ejemplo anterior usando correlaciones (coeficiente de correlación de Pearson y correlación de rangos de Spearman).
Paso 4: Conclusión
Conclusión de la prueba para la pendiente: Con base en el diagrama de dispersión y el análisis de regresión lineal, dado que la relación es lineal y el valor p = 0.0124, existe una relación lineal positiva estadísticamente significativa entre el recuento de llanto recién nacido y el coeficiente intelectual a los 3 años.
Interpretación de R-cuadrado: Con base en nuestra R 2 y diagrama de dispersión, la relación es algo débil, ya que solo 16.1% de la variación en el puntaje de CI a los tres años se explica por nuestro modelo de regresión lineal utilizando el recuento de llantos recién nacidos.
Interpretación de la pendiente: Por cada incremento de 1 unidad en el conteo de llanto, se espera que el coeficiente intelectual medio poblacional aumente en 1.54 puntos, sin embargo, el intervalo de confianza del 95% sugiere que este valor podría ser tan bajo como 0.35 puntos hasta tan alto como 2.72 puntos.
EJEMPLO: Gestación vs. longevidad en animales
Volvemos a los datos de una actividad anterior (Aprender haciendo — Correlación y valores atípicos (Software)). El período promedio de gestación, o tiempo de embarazo, de un animal está estrechamente relacionado con su longevidad, la duración de su vida útil. Se han registrado datos sobre el periodo promedio de gestación y longevidad (en cautiverio) de 40 especies diferentes de animales. Aquí hay un resumen de las variables en nuestro conjunto de datos:
- animal: el nombre de la especie animal.
- gestación: el período promedio de gestación de la especie, en días.
- longevidad: la longevidad promedio de la especie, en años.
En este caso, ya sea que incluyamos el valor atípico o no, existe un problema de varianza no constante. Se puede ver claramente que, en general, a medida que aumenta la longevidad, aumenta la variación de la gestación.
Estos datos no son particularmente buenos candidatos para el análisis de regresión lineal simple (sin modificaciones adicionales como transformaciones o el uso de métodos alternativos).
El coeficiente de correlación de Pearson (o correlación de rango de Spearman), aún puede proporcionar una medida razonable de la fuerza de la relación, que es claramente una relación positiva de la trama de dispersión y nuestra medida de correlación anterior.
Salida — Contiene diagramas de dispersión con ecuaciones lineales y curvas LOESS (promedio lineal) para el dataset con y sin el valor atípico. Preste especial atención al problema con la varianza no constante que se ve en estas gráficas de dispersión.
EJEMPLO: Primas de seguros
Los datos utilizados en el análisis que se proporcionan a continuación contienen las primas mensuales, la experiencia de manejo y el género para una muestra aleatoria de conductores.
Para analizar estos datos, hemos visto a machos y hembras como dos grupos separados y hemos estimado la correlación y la ecuación de regresión lineal para cada género. Deseamos predecir la prima mensual utilizando años de experiencia de manejo.
Utilice esta salida para la práctica adicional con estos conceptos. Para cada género considera lo siguiente:
- ¿Están satisfechos los supuestos?
- ¿La correlación es estadísticamente significativa? ¿Es positivo o negativo? ¿Débil o fuerte?
- ¿La pendiente es estadísticamente significativa? ¿Qué significa la pendiente en contexto? ¿Cuál es el intervalo de confianza para la pendiente?
- ¿Qué es R 2 y qué significa en contexto?

