Acabamos de completar la parte del curso sobre los métodos inferenciales para las relaciones entre variables. El objetivo general de inferencia para las relaciones es evaluar si los datos observados proporcionan evidencia de una relación significativa entre las dos variables (es decir, una relación verdadera que existe en la población).
Al igual que la unidad sobre relaciones en la unidad de Análisis Exploratorio de Datos (EDA), esta parte del curso se organizó de acuerdo con la clasificación de roles y tipos de las dos variables involucradas.
Sin embargo, a diferencia de la unidad EDA, cuando se trata de métodos inferenciales, distinguimos además entre tres subcasos en el caso C→Q, por lo que esencialmente cubrimos 5 casos en total.
La siguiente tabla muy detallada de clasificación de tipos de roles resume tanto EDA como inferencia para la relación entre variables:
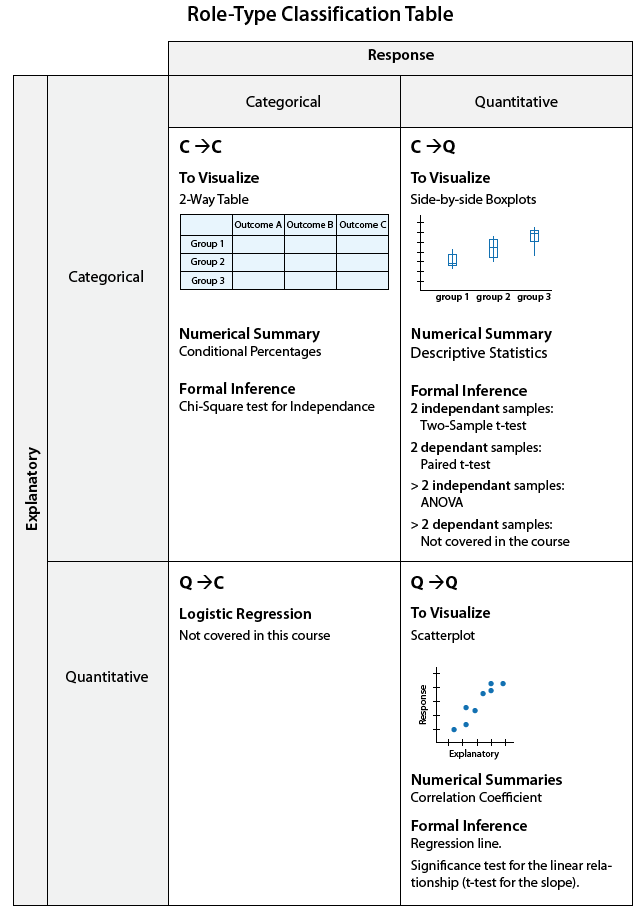
Caso C-Q
Aquí un resumen de las pruebas para el escenario donde k = 2.
|
Muestras independientes (más énfasis)
|
Muestras Dependientes (Menos Énfasis)
|
Pruebas estándar
- Prueba T de dos muestras asumiendo varianzas iguales
- Prueba T de dos muestras asumiendo varianzas desiguales
Prueba no paramétrica
- Prueba U de Mann-Whitney (o Wilcoxon Rank-Sum)
|
Prueba estándar
Pruebas no paramétricas
- Prueba de Signo
- Prueba de rango firmado por Wilcoxon
|
Aquí un resumen de las pruebas para el escenario donde k > 2.
|
Muestras Independientes (Solo Énfasis)
|
Muestras dependientes (no discutidas)
|
Pruebas estándar
- ANOVA unidireccional (Análisis de varianza)
Prueba no paramétrica
- ANOVA de una vía Kruskal—Wallis
|
Prueba estándar
- ANOVA de medidas repetidas (o similar)
|
Caso C-C
|
Muestras Independientes (Solo Énfasis)
|
Muestras dependientes (no discutidas)
|
Pruebas estándar
- Prueba de Chi-cuadrado corregida de continuidad para la independencia (caso 2×2)
- Prueba de Chi-cuadrado para la independencia (caso RxC)
Prueba no paramétrica
|
Prueba estándar
- Prueba de McNemar — Caso 2×2
|
Caso Q-Q
|
Muestras Independientes (Solo Énfasis)
|
Muestras dependientes (no discutidas)
|
Pruebas estándar
- Prueba de significancia del coeficiente de correlación de Pearson
- Prueba de significancia de la pendiente en regresión lineal
Prueba no paramétrica
- Prueba de significancia de la correlación de rangos de Spearman
|
Prueba estándar
- No Cubierto (Análisis Longitudinal de Datos, etc.)
|


