1.2: El cuento de precaución de la paradoja de Simpson
- Page ID
- 151899
La siguiente es una historia real (creo que...). En 1973, la Universidad de California, Berkeley tenía algunas preocupaciones sobre las admisiones de estudiantes a sus cursos de posgrado. Específicamente, lo que causó el problema fue que el desglose por género de sus admisiones, que se veían así...
| Número de aspirantes | Porcentaje admitido | |
|---|---|---|
| Machos | 8442 | 46% |
| Hembras | 4321 | 35% |
... y los estaban preocupados por ser demandados. 4 Dado que había cerca de 13 mil aspirantes, una diferencia de 9% en las tasas de admisión entre hombres y mujeres es demasiado grande para ser una coincidencia. Datos bastante convincentes, ¿verdad? Y si te dijera que estos datos reflejan en realidad un sesgo débil a favor de las mujeres (¡más o menos!) , probablemente pensarías que yo era una locura o sexista.
Curiosamente, en realidad es cierto... cuando la gente empezó a mirar más cuidadosamente los datos de admisiones (Bickel, Hammel y O'Connell 1975) contaban una historia bastante diferente. Específicamente, cuando lo miraron departamento por departamento, resultó que la mayoría de los departamentos en realidad tenían una tasa de éxito ligeramente mayor para las aspirantes femeninas que para las aspirantes masculinas. En el cuadro 1.1 se muestran las cifras de admisión para los seis departamentos más grandes (con los nombres de los departamentos eliminados por razones de privacidad):
Cuadro 1.1: Cifras de admisión para los seis departamentos más grandes por género
| Departamento | Solicitantes Masculinos | Porcentaje Masculino Admitido | Solicitantes Femeninas | Porcentaje de mujeres admitidas |
|---|---|---|---|---|
| A | 825 | 62% | 108 | 82% |
| B | 560 | 63% | 25 | 68% |
| C | 325 | 37% | 593 | 34% |
| D | 417 | 33% | 375 | 35% |
| E | 191 | 28% | 393 | 24% |
| F | 272 | 6% | 341 | 7% |
Sorprendentemente, ¡la mayoría de los departamentos tuvieron una mayor tasa de ingresos para las mujeres que para los hombres! Sin embargo, la tasa general de ingreso en la universidad para las mujeres fue menor que para los hombres. ¿Cómo puede ser esto? ¿Cómo pueden ser veraces ambas afirmaciones al mismo tiempo?
Esto es lo que está pasando. En primer lugar, observe que los departamentos no son iguales entre sí en términos de sus porcentajes de admisión: algunos departamentos (por ejemplo, ingeniería, química) tendían a admitir un alto porcentaje de los aspirantes calificados, mientras que otros (por ejemplo, el inglés) tendían a rechazar la mayoría de los candidatos, aunque fueran de alta calidad. Entonces, entre los seis departamentos arriba indicados, observe que el departamento A es el más generoso, seguido por B, C, D, E y F en ese orden. A continuación, observe que machos y hembras tendían a postularse a diferentes departamentos. Si clasificamos los departamentos en términos del número total de aspirantes masculinos, obtenemos A > B>D>C>F>E (los departamentos “fáciles” están en negrita). En conjunto, los varones tendían a postularse a los departamentos que tenían altas tasas de ingreso. Ahora compara esto con cómo se distribuyeron las aspirantes femeninas. La clasificación de los departamentos en términos del número total de mujeres aspirantes produce un ordenamiento bastante diferente C>E>D>F> A > B. Es decir, lo que estos datos parecen sugerir es que las aspirantes solían postularse a departamentos “más duros”. Y de hecho, si nos fijamos en toda la Figura 1.1 vemos que esta tendencia es sistemática, y bastante llamativa. Este efecto se conoce como la paradoja de Simpson. No es común, pero sí sucede en la vida real, y la mayoría de las personas se sorprenden mucho cuando lo encuentran por primera vez, y muchas personas se niegan incluso a creer que es real. Es muy real. Y si bien hay muchas lecciones estadísticas muy sutiles enterradas ahí, quiero usarla para hacer un punto mucho más importante... investigar es difícil, y hay muchas trampas sutiles y contradictorias que acechan a los incautos. Esa es la razón #2 por qué a los científicos les encantan las estadísticas, y por qué enseñamos métodos de investigación Porque la ciencia es dura, y la verdad a veces se esconde astutamente en los rincones y recovecos de datos complicados.
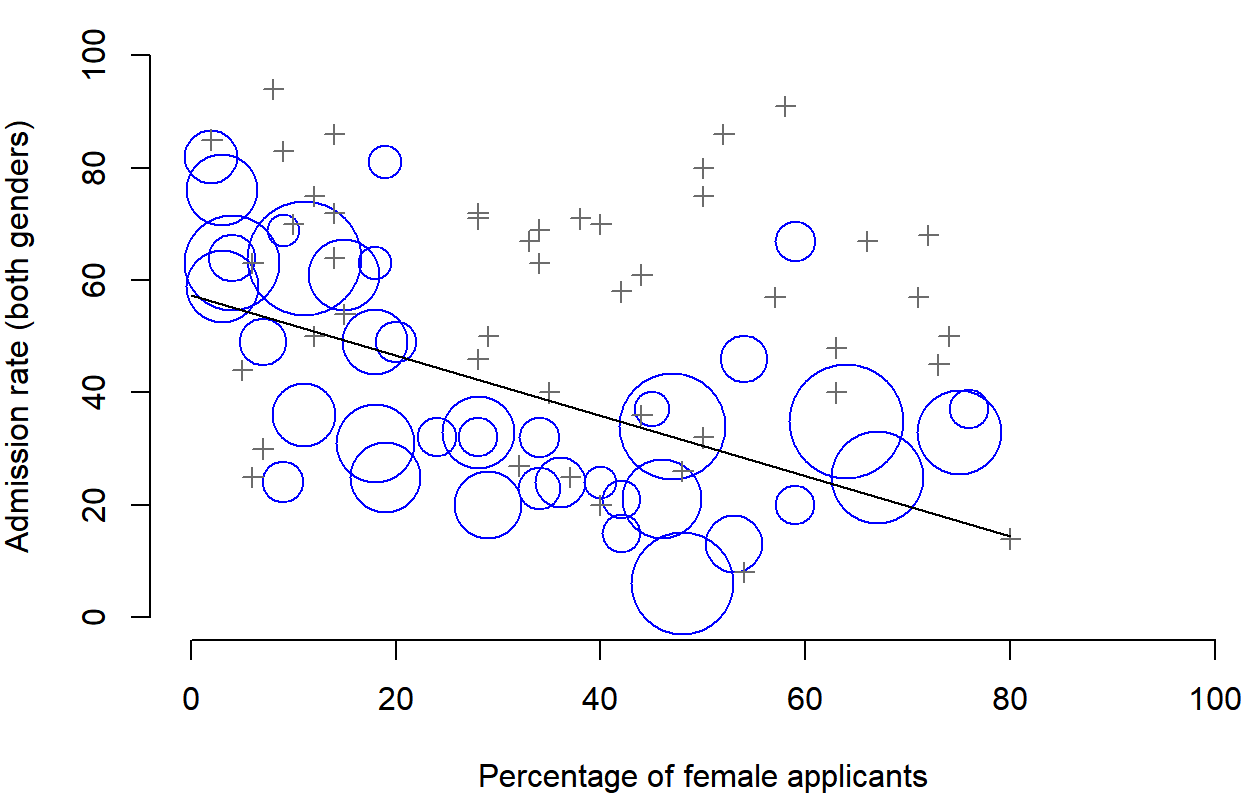
Antes de dejar este tema por completo, quiero señalar algo más realmente crítico que a menudo se pasa por alto en una clase de métodos de investigación. La estadística solo resuelve parte del problema. Recuerden que iniciamos todo esto con la preocupación de que los procesos de admisión de Berkeley pudieran estar injustamente sesgados contra las aspirantes femeninas. Cuando miramos los datos “agregados”, sí parecía que la universidad discriminaba a las mujeres, pero cuando “desagregamos” y miramos el comportamiento individual de todos los departamentos, resultó que los departamentos reales estaban, en todo caso, ligeramente sesgados a favor de las mujeres. El sesgo de género en las admisiones totales se debió a que las mujeres tendían a autoseleccionar para departamentos más duros. Desde una perspectiva jurídica, eso probablemente pondría a la universidad en claro. Las admisiones de posgrado se determinan a nivel del departamento individual (y hay buenas razones para hacerlo), y a nivel de departamentos individuales, las decisiones son más o menos imparciales (el sesgo débil a favor de las mujeres en ese nivel es pequeño, y no consistente entre departamentos). Dado que la universidad no puede dictar a qué departamentos la gente elige postularse, y la toma de decisiones se lleva a cabo a nivel del departamento, difícilmente se le puede responsabilizar de los sesgos que esas elecciones produzcan.
Esa fue la base de mis comentarios algo simples antes, pero esa no es exactamente toda la historia, ¿verdad? Después de todo, si nos interesa esto desde una perspectiva más sociológica y psicológica, podríamos preguntarnos por qué existen diferencias de género tan fuertes en las aplicaciones. ¿Por qué los hombres tienden a aplicar a la ingeniería con más frecuencia que las mujeres, y por qué esto se invierte para el departamento de inglés? ¿Y por qué ocurre que los departamentos que tienden a tener un sesgo de solicitud femenina tienden a tener tasas de admisión generales más bajas que aquellos departamentos que tienen un sesgo de solicitud masculina? ¿Podría esto no reflejar todavía un sesgo de género, a pesar de que cada departamento es imparcial en sí mismo? Podría. Supongamos, hipotéticamente, que los varones prefirieron aplicar a las “ciencias duras” y las mujeres prefieren las “humanidades”. Y supongamos además que la razón por la que los departamentos de humanidades tienen bajas tasas de admisión es porque el gobierno no quiere financiar las humanidades (los lugares de doctorado, por ejemplo, suelen estar vinculados a proyectos de investigación financiados por el gobierno). ¿Eso constituye un sesgo de género? ¿O simplemente una visión poco iluminada del valor de las humanidades? Y si alguien de alto nivel en el gobierno recortara los fondos de humanidades porque sintieran que las humanidades son “cosas inútiles de pollito”. Eso parece bastante descaradamente sesgado de género. Nada de esto entra en el ámbito de la estadística, pero es importante para el proyecto de investigación. Si estás interesado en los efectos estructurales generales de los sesgos sutiles de género, entonces probablemente quieras mirar tanto los datos agregados como los desagregados. Si estás interesado en el proceso de toma de decisiones en el propio Berkeley entonces probablemente solo te interesen los datos desagregados.
En definitiva hay muchas preguntas críticas que no puedes responder con estadísticas, pero las respuestas a esas preguntas tendrán un enorme impacto en la forma en que analizas e interpretas los datos. Y esta es la razón por la que siempre debes pensar en la estadística como una herramienta para ayudarte a conocer tus datos, ni más ni menos. Es una herramienta poderosa para ese fin, pero no hay sustituto para el pensamiento cuidadoso.


