5.2: Medidas de Variabilidad
- Page ID
- 151551
Las estadísticas que hemos discutido hasta ahora se refieren todas a la tendencia central. Es decir, todos hablan de qué valores están “en el medio” o “populares” en los datos. Sin embargo, la tendencia central no es el único tipo de estadística resumida que queremos calcular. Lo segundo que realmente queremos es una medida de la variabilidad de los datos. Es decir, ¿qué tan “dispersos” están los datos? ¿Qué tan “lejos” de la media o mediana tienden a estar los valores observados? Por ahora, supongamos que los datos son escala de intervalo o ratio, por lo que seguiremos usando los datos afl.margins. Utilizaremos estos datos para discutir varias medidas diferentes de propagación, cada una con diferentes fortalezas y debilidades.
Rango
El rango de una variable es muy simple: es el valor más grande menos el valor más pequeño. Para los datos de márgenes ganadores de AFL, el valor máximo es 116, y el valor mínimo es 0. Podemos calcular estos valores en R usando las funciones max () y min ():
max( afl.margins )## [1] 116min( afl.margins )
## [1] 0donde he omitido la salida porque no es interesante. La otra posibilidad es usar la función range (); que genera tanto el valor mínimo como el valor máximo en un vector, así:
range( afl.margins )
## [1] 0 116Aunque el rango es la forma más sencilla de cuantificar la noción de “variabilidad”, es una de las peores. Recordemos de nuestra discusión sobre la media que queremos que nuestra medida sumaria sea robusta. Si el conjunto de datos tiene uno o dos valores extremadamente malos en él, nos gustaría que nuestras estadísticas no se vieran influenciadas indebidamente por estos casos. Si volvemos a mirar nuestro ejemplo de juguete de un conjunto de datos que contiene valores atípicos muy extremos...
−100,2,3,4,5,6,7,8,9,10
... está claro que el rango no es robusto, ya que este tiene un rango de 110, pero si se eliminara el valor atípico tendríamos un rango de sólo 8.
Gama intercuartil
El rango intercuartílico (IQR) es como el rango, pero en lugar de calcular la diferencia entre el valor más grande y el más pequeño, calcula la diferencia entre el cuantil 25 y el cuantil 75. Probablemente ya sabes lo que es un cuantil (se llaman más comúnmente percentiles), pero si no: el percentil 10 de un conjunto de datos es el número más pequeño x de tal manera que el 10% de los datos es menor que x De hecho, ya nos hemos topado con la idea: la mediana de un conjunto de datos es su cuantil/percentil 50! R en realidad te proporciona una forma de calcular cuantiles, usando la función (sorpresa, sorpresa) quantile (). Usémoslo para calcular la mediana del margen ganador de AFL:
quantile( x = afl.margins, probs = .5)## 50%
## 30.5Y no en vano, esto concuerda con la respuesta que vimos antes con la función median (). Ahora, en realidad podemos ingresar muchos cuantiles a la vez, especificando un vector para el argumento probs. Así que vamos a hacer eso, y obtener el percentil 25 y 75:
quantile( x = afl.margins, probs = c(.25,.75) )## 25% 75%
## 12.75 50.50Y, al señalar que 50.5−12.75=37.75, podemos ver que el rango intercuartil para los datos de márgenes ganadores de la AFL 2010 es de 37.75. Por supuesto, eso parece demasiado trabajo para hacer todo ese tipo de mecanografía, así que R tiene una función incorporada llamada IQR () que podemos usar:
IQR( x = afl.margins )## [1] 37.75Si bien es obvio cómo interpretar el rango, es un poco menos obvio cómo interpretar el IQR. La forma más sencilla de pensarlo es así: el rango intercuartílico es el rango abarcado por la “mitad media” de los datos. Es decir, una cuarta parte de los datos cae por debajo del percentil 25, una cuarta parte de los datos está por encima del percentil 75, dejando la “mitad media” de los datos entre los dos. Y el IQR es el rango que cubre esa mitad media.
Desviación media absoluta
Las dos medidas que hemos analizado hasta ahora, el rango y el rango intercuartílico, ambas se basan en la idea de que podemos medir la propagación de los datos observando los cuantiles de los datos. Sin embargo, esta no es la única manera de pensar sobre el problema. Un enfoque diferente es seleccionar un punto de referencia significativo (generalmente la media o la mediana) y luego reportar las desviaciones “típicas” de ese punto de referencia. ¿Qué entendemos por desviación “típica”? Por lo general, ¡el valor medio o mediano de estas desviaciones! En la práctica, esto conduce a dos medidas diferentes, la “desviación absoluta media (de la media)” y la “desviación absoluta mediana (de la mediana)”. Por lo que he leído, la medida basada en la mediana parece ser utilizada en estadística, y sí parece ser la mejor de las dos, pero para ser honesto no creo que la haya visto utilizada mucho en psicología. Sin embargo, la medida basada en la media aparece ocasionalmente en psicología. En esta sección hablaré del primero, y luego volveré a hablar del segundo.
Como el párrafo anterior puede sonar un poco abstracto, pasemos un poco más lentamente por la desviación absoluta media de la media. Una cosa útil de esta medida es que el nombre en realidad te dice exactamente cómo calcularla. Pensemos en nuestros datos de márgenes ganadores de AFL, y una vez más comenzaremos fingiendo que solo hay 5 juegos en total, con márgenes ganadores de 56, 31, 56, 8 y 32. Dado que nuestros cálculos se basan en un examen de la desviación de algún punto de referencia (en este caso la media), lo primero que necesitamos calcular es la media,\(\bar{X}\). Para estas cinco observaciones, nuestra media es\(\bar{X}\) =36.6. El siguiente paso es convertir cada una de nuestras observaciones X i en una puntuación de desviación. Esto lo hacemos calculando la diferencia entre la observación Xi y la media\(\bar{X}\). Es decir, la puntuación de desviación se define como X i −\(\bar{X}\). Para la primera observación en nuestra muestra, esto es igual a 56−36.6=19.4. Bien, eso es bastante simple. El siguiente paso en el proceso es convertir estas desviaciones en desviaciones absolutas. Como comentamos anteriormente al hablar de la función abs () en R (Sección 3.5), lo hacemos convirtiendo cualquier valor negativo a positivo. Matemáticamente, denotaríamos el valor absoluto de −3 como |−3|, y así decimos que |−3|=3. Usamos la función de valor absoluto aquí porque realmente no nos importa si el valor es mayor que la media o menor que la media, solo nos interesa lo cerca que está de la media. Para ayudar a que este proceso sea lo más obvio posible, la siguiente tabla muestra estos cálculos para las cinco observaciones:
| la observación | su símbolo | el valor observado |
|---|---|---|
| margen ganador, juego 2 | X2 | 31 puntos |
| margen ganador, juego 5 | X5 | 32 puntos |
| margen ganador, juego 1 | X1 | 56 puntos |
| margen ganador, juego 3 | X3 | 56 puntos |
| margen ganador, juego 4 | X4 | 8 puntos |
Ahora que hemos calculado la puntuación de desviación absoluta para cada observación en el conjunto de datos, todo lo que tenemos que hacer para calcular la media de estas puntuaciones. Hagámoslo:
\ [
\ dfrac {19.4+5.6+19.4+28.6+4.6} {5} =15.52
\ nonumber\]
Y ya terminamos. La desviación media absoluta para estas cinco puntuaciones es de 15.52.
No obstante, si bien nuestros cálculos para este pequeño ejemplo están llegando a su fin, sí nos quedan un par de cosas de las que hablar. En primer lugar, realmente deberíamos tratar de escribir una fórmula matemática adecuada. Pero para hacer esto necesito alguna notación matemática para referirme a la desviación media absoluta. Irritantemente, “desviación media absoluta” y “mediana de desviación absoluta” tienen el mismo acrónimo (MAD), lo que lleva a cierta cantidad de ambigüedad, y dado que R tiende a usar MAD para referirse a la desviación media absoluta, será mejor que se me ocurra algo diferente para la desviación absoluta media. Suspiro. Lo que voy a hacer es usar AAD en su lugar, abreviatura de desviación absoluta promedio. Ahora que tenemos alguna notación inequívoca, aquí está la fórmula que describe lo que acabamos de calcular:
\ [
(X) =\ dfrac {1} {N}\ suma_ {i=1} ^ {N}\ izquierda|x_ {i} -\ bar {X}\ derecha|
\ nonumber\]
Lo último de lo que tenemos que hablar es cómo calcular AAD en R. Una posibilidad sería hacer todo usando comandos de bajo nivel, siguiendo laboriosamente los mismos pasos que utilicé al describir los cálculos anteriores. Sin embargo, eso es bastante tedioso. Terminarías con una serie de comandos que podrían verse así:
X <- c(56, 31,56,8,32) # enter the data
X.bar <- mean( X ) # step 1. the mean of the data
AD <- abs( X - X.bar ) # step 2. the absolute deviations from the mean
AAD <- mean( AD ) # step 3. the mean absolute deviations
print( AAD ) # print the results## [1] 15.52Cada uno de esos comandos es bastante simple, pero solo hay demasiados de ellos. Y porque me parece que es demasiado mecanografiar, el paquete lsr tiene una función muy simple llamada aad () que hace los cálculos por ti. Si aplicamos la función aad () a nuestros datos, obtenemos esto:
library(lsr)
aad( X )## [1] 15.52No hay sorpresa ahí.
Varianza
Aunque la medida de desviación absoluta media tiene sus usos, no es la mejor medida de variabilidad para usar. Desde una perspectiva puramente matemática, hay algunas razones sólidas para preferir desviaciones cuadradas en lugar de desviaciones absolutas. Si hacemos eso, obtenemos una medida que se llama varianza, que tiene muchas propiedades estadísticas realmente agradables que voy a ignorar, 71 (X) $ y Var (Y) respectivamente. Ahora imagina que quiero definir una nueva variable Z que es la suma de las dos, Z=X+Y. Resulta que la varianza de Z es igual a Var (X) +Var (Y). Esta es una propiedad muy útil, pero no es cierto de las otras medidas de las que hablo en esta sección.] y una falla psicológica masiva del que voy a hacer un gran problema en un momento. La varianza de un conjunto de datos X a veces se escribe como Var (X), pero se denota más comúnmente s 2 (la razón de esto se aclarará en breve). La fórmula que utilizamos para calcular la varianza de un conjunto de observaciones es la siguiente:
\ [
\ begin {alineado}
&\ nombreoperador {Var} (X) =\ dfrac {1} {N}\ suma_ {i=1} ^ {N}\ left (X_ {i} -\ bar {X}\ derecha) ^ {2}\\
&\ nombre_operador {Var} (X) =\ dfrac {\ sum_ {i=1} ^ {N}\ izquierda (X_ {i} -\ bar {X}\ derecha) ^ {2}} {N}
\ final {alineado}
\ nonumber\]
Como puedes ver, básicamente es la misma fórmula que usamos para calcular la desviación media absoluta, excepto que en lugar de usar “desviaciones absolutas” usamos “desviaciones cuadradas”. Es por esta razón que a la varianza se le denomina a veces la “desviación cuadrática media”.
Ahora que tenemos la idea básica, echemos un vistazo a un ejemplo concreto. Una vez más, usemos los cinco primeros juegos de AFL como nuestros datos. Si seguimos el mismo enfoque que tomamos la última vez, terminamos con la siguiente tabla:
Cuadro 5.1: Operaciones aritméticas básicas en R. Estos cinco operadores se utilizan con mucha frecuencia a lo largo del texto, por lo que es importante estar familiarizado con ellos desde el principio.
| Notación [Inglés] | i [qué juego] | X i [valor] | X i −\(\bar{X}\) [desviación de la media] | (Xi−\(\bar{X}\)) 2 [desviación absoluta] |
|---|---|---|---|---|
| 5 | 32 | -4.6 | 21.16 | |
| 2 | 31 | -5.6 | 31.36 | |
| 1 | 56 | 19.4 | 376.36 | |
| 3 | 56 | 19.4 | 376.36 | |
| 4 | 8 | -28.6 | 817.96 |
Esa última columna contiene todas nuestras desviaciones cuadradas, así que todo lo que tenemos que hacer es promediarlas. Si lo hacemos escribiendo todos los números en R a mano...
( 376.36 + 31.36 + 376.36 + 817.96 + 21.16 ) / 5
## [1] 324.64... terminamos con una varianza de 324.64. Emocionante, ¿no? Por el momento, ignoremos la pregunta candente que probablemente todos ustedes estén pensando (es decir, ¿qué diablos significa realmente una varianza de 324.64?) y en cambio hablar un poco más sobre cómo hacer los cálculos en R, porque esto revelará algo muy raro.
Como siempre, queremos evitar tener que teclear muchos números nosotros mismos. Y como sucede, tenemos el vector X tirado alrededor, que creamos en la sección anterior. Con esto en mente, podemos calcular la varianza de X usando el siguiente comando,
mean( (X - mean(X) )^2)
## [1] 324.64y como de costumbre obtenemos la misma respuesta que la que obtuvimos cuando hicimos todo a mano. No obstante, sigo pensando que esto es demasiado mecanografiar. Afortunadamente, R tiene una función incorporada llamada var () que calcula varianzas. Entonces también podríamos hacer esto...
var(X)
## [1] 405.8y obtienes lo mismo... no, espera... obtienes una respuesta completamente diferente. Eso es raro. ¿R está rota? ¿Es esto un error tipográfico? ¿Dan es un idiota?
Como sucede, la respuesta es no. 72 No es un error tipográfico, y R no está cometiendo un error. Para tener una idea de lo que está sucediendo, dejemos de usar el pequeño conjunto de datos que contiene solo 5 puntos de datos y cambiemos al conjunto completo de 176 juegos que tenemos almacenados en nuestro vector afl.margins. Primero, calculemos la varianza usando la fórmula que describí anteriormente:
mean( (afl.margins - mean(afl.margins) )^2)## [1] 675.9718Ahora usemos la función var ():
var( afl.margins )## [1] 679.8345Hm. Estos dos números son muy similares esta vez. Eso parece demasiada coincidencia para ser un error. Y claro que no es un error. De hecho, es muy sencillo explicar lo que R está haciendo aquí, pero un poco más complicado para explicar por qué R lo está haciendo. Entonces comencemos con el “qué”. Lo que R está haciendo es evaluar una fórmula ligeramente diferente a la que te mostré anteriormente. En lugar de promediar las desviaciones cuadradas, lo que requiere dividir por el número de puntos de datos N, R ha optado por dividir por N−1. En otras palabras, la fórmula que R está usando es esta
\ [
\ dfrac {1} {N-1}\ suma_ {i=1} ^ {N}\ izquierda (X_ {i} -\ bar {X}\ derecha) ^ {2}
\ nonúmero$$
Es bastante fácil verificar que esto es lo que está sucediendo, como lo ilustra el siguiente comando:
sum( (X-mean(X))^2 ) / 4## [1] 405.8Esta es la misma respuesta que R nos dio originalmente cuando calculamos var (X) originalmente. Entonces ese es el qué. La verdadera pregunta es por qué R está dividiendo por N−1 y no por N. Después de todo, se supone que la varianza es la desviación cuadrática media, ¿verdad? Entonces, ¿no deberíamos estar dividiendo por N, el número real de observaciones en la muestra? Bueno, sí, deberíamos. Sin embargo, como discutiremos en el capítulo 10, existe una sutil distinción entre “describir una muestra” y “hacer conjeturas sobre la población de la que procede la muestra”. Hasta este punto, ha sido una distinción sin diferencia. Independientemente de si estás describiendo una muestra o haciendo inferencias sobre la población, la media se calcula exactamente de la misma manera. No así para la varianza, o la desviación estándar, o para muchas otras medidas además. Lo que le describí inicialmente (es decir, tomar el promedio real, y así dividir por N) asume que literalmente tiene la intención de calcular la varianza de la muestra. La mayoría de las veces, sin embargo, no estás terriblemente interesado en la muestra en sí misma. Más bien, la muestra existe para decirte algo sobre el mundo. Si es así, en realidad estás empezando a dejar de calcular una “estadística de muestra”, y hacia la idea de estimar un “parámetro de población”. No obstante, me estoy adelantando. Por ahora, solo tomemos con fe que R sabe lo que está haciendo, y volveremos a examinar la pregunta más adelante cuando hablemos de estimación en el Capítulo 10.
Bien, una última cosa. Esta sección hasta el momento se ha leído un poco como una novela de misterio. Te he mostrado cómo calcular la varianza, describí lo raro de “N−1" que hace R e insinué la razón por la que está ahí, pero no he mencionado lo único más importante... ¿cómo interpretas la varianza? Se supone que las estadísticas descriptivas describen las cosas, después de todo, y ahora mismo la varianza es realmente solo un número galimatías. Desafortunadamente, la razón por la que no te he dado la interpretación amigable con los humanos de la varianza es que realmente no hay una. Este es el problema más grave con la varianza. Aunque tiene algunas propiedades matemáticas elegantes que sugieren que realmente es una cantidad fundamental para expresar variación, es completamente inútil si quieres comunicarte con un humano real... ¡las variaciones son completamente ininterpretables en términos de la variable original! Todos los números han sido cuadrados, y ya no significan nada. Este es un tema enorme. Por ejemplo, según la tabla que presenté anteriormente, el margen en el juego 1 fue “376.36 puntos-cuadrados más alto que el margen promedio”. Esto es exactamente tan estúpido como suena; y así cuando calculamos una varianza de 324.64, estamos en la misma situación. He visto muchos juegos de foty, y nunca nadie se ha referido a “puntos al cuadrado”. No es una unidad de medida real, y como la varianza se expresa en términos de esta unidad galimatías, carece totalmente de sentido para un humano.
Desviación estándar
Bien, supongamos que te gusta la idea de usar la varianza por esas buenas propiedades matemáticas de las que no he hablado, pero —como eres humano y no un robot— te gustaría tener una medida que se exprese en las mismas unidades que los datos en sí (es decir, puntos, no puntos al cuadrado). ¿Qué debes hacer? La solución al problema es obvia: tomar la raíz cuadrada de la varianza, conocida como la desviación estándar, también llamada la “desviación media cuadrática de raíz”, o RMSD. Esto resuelve el problema de manera bastante clara: si bien nadie tiene idea de lo que realmente significa “una varianza de 324.68 puntos cuadrados”, es mucho más fácil entender “una desviación estándar de 18.01 puntos”, ya que se expresa en las unidades originales. Es tradicional referirse a la desviación estándar de una muestra de datos como s, aunque en ocasiones también se utilizan “sd” y “std dev.” Debido a que la desviación estándar es igual a la raíz cuadrada de la varianza, probablemente no te sorprenderá ver que la fórmula es:
\ [
s=\ sqrt {\ dfrac {1} {N}\ suma_ {i=1} ^ {N}\ izquierda (X_ {i} -\ bar {X}\ derecha) ^ {2}}
\ nonumber\]
y la función R que usamos para calcularla es sd (). Sin embargo, como habrás adivinado de nuestra discusión sobre la varianza, lo que R realmente calcula es ligeramente diferente a la fórmula dada anteriormente. Al igual que el que vimos con la varianza, lo que R calcula es una versión que divide por N−1 en lugar de N. Por razones que tendrán sentido cuando volvamos a este tema en Capítulo @refch:estimación me referiré a esta nueva cantidad como\(\hat{\sigma}\) (léase: “sigma hat”), y la fórmula para esto es
\ [
\ hat {\ sigma} =\ sqrt {\ dfrac {1} {N-1}\ suma_ {i=1} ^ {N}\ izquierda (X_ {i} -\ bar {X}\ derecha) ^ {2}}
\ nonumber\]
Con eso en mente, calcular las desviaciones estándar en R es simple:
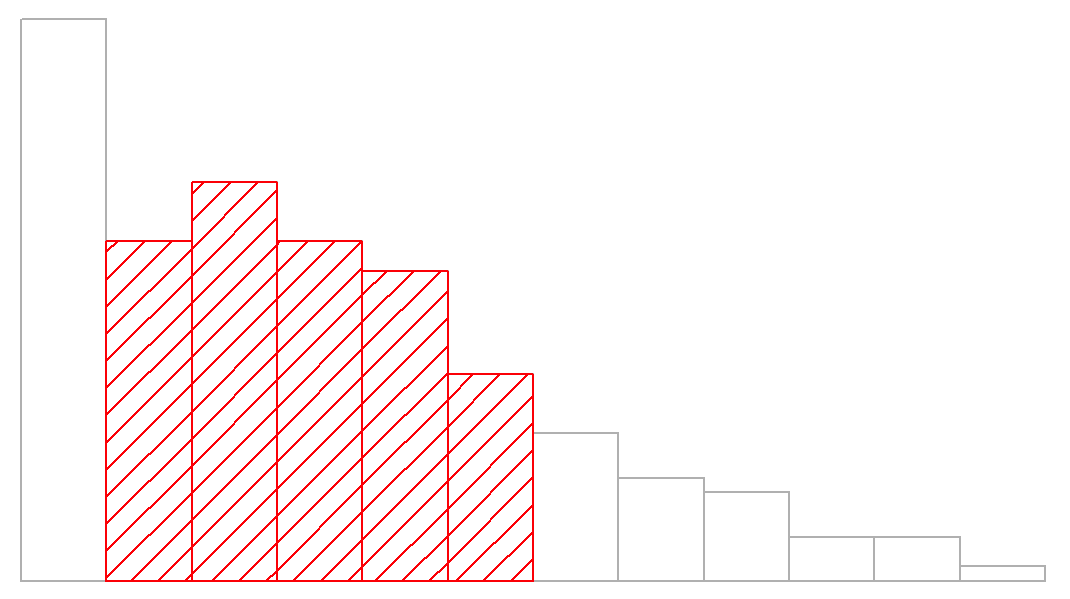
sd( afl.margins ) ## [1] 26.07364Interpretar las desviaciones estándar es un poco más complejo. Debido a que la desviación estándar se deriva de la varianza, y la varianza es una cantidad que tiene poco o ningún significado que tenga sentido para nosotros los humanos, la desviación estándar no tiene una interpretación simple. Como consecuencia, la mayoría de nosotros simplemente confiamos en una regla general simple: en general, se debe esperar que el 68% de los datos caigan dentro de 1 desviación estándar de la media, el 95% de los datos estén dentro de 2 desviaciones estándar de la media y el 99.7% de los datos se encuentren dentro de 3 desviaciones estándar de la media. Esta regla tiende a funcionar bastante bien la mayor parte del tiempo, pero no es exacta: en realidad se calcula basándose en una suposición de que el histograma es simétrico y “en forma de campana”. 73 Como puede ver al observar el histograma de márgenes ganadores de AFL en la Figura 5.1, ¡esto no es exactamente cierto para nuestros datos! Aun así, la regla es aproximadamente correcta. Resulta que 65.3% de los datos de márgenes de AFL se encuentran dentro de una desviación estándar de la media. Esto se muestra visualmente en la Figura 5.3.
Desviación absoluta mediana
La última medida de variabilidad de la que quiero hablar es la mediana de la desviación absoluta (MAD). La idea básica detrás de MAD es muy simple, y es prácticamente idéntica a la idea detrás de la desviación media absoluta (Sección 5.2.3). La diferencia es que usas la mediana en todas partes. Si tuviéramos que enmarcar esta idea como un par de comandos R, se verían así:
# mean absolute deviation from the mean:
mean( abs(afl.margins - mean(afl.margins)) )## [1] 21.10124
# *median* absolute deviation from the *median*:
median( abs(afl.margins - median(afl.margins)) )## [1] 19.5Esto tiene una interpretación sencilla: cada observación en el conjunto de datos se encuentra a cierta distancia del valor típico (la mediana). Entonces el MAD es un intento de describir una desviación típica de un valor típico en el conjunto de datos. No sería irrazonable interpretar el valor MAD de 19.5 para nuestros datos de AFL diciendo algo como esto:
El margen medio ganador en 2010 fue de 30.5, lo que indica que un juego típico implicaba un margen ganador de unos 30 puntos. No obstante, hubo una buena cantidad de variación de un juego a otro: el valor de MAD fue de 19.5, lo que indica que un margen ganador típico diferiría de este valor medio en unos 19-20 puntos.
Como era de esperar, R tiene una función incorporada para calcular MAD, y sin duda te sorprenderá escuchar que se llama mad (). Sin embargo, es un poco más complicado que las funciones que hemos estado usando anteriormente. Si quieres usarlo para calcular MAD exactamente de la misma manera que lo he descrito anteriormente, el comando que necesitas usar especifica dos argumentos: el conjunto de datos en sí x, y una constante que explicaré en un momento. Para nuestros propósitos, la constante es 1, por lo que nuestro mando se convierte en
mad( x = afl.margins, constant = 1 )## [1] 19.5Aparte de la rareza de tener que escribir esa constante = 1 parte, esto es bastante sencillo.
Bien, entonces, ¿qué es exactamente esta constante = 1 argumento? No voy a entrar en todos los detalles aquí, pero aquí está la esencia. Aunque el valor MAD “crudo” que he descrito anteriormente es completamente interpretable en sus propios términos, en realidad no es así como se usa en muchos contextos del mundo real. En cambio, lo que pasa mucho es que el investigador realmente quiere calcular la desviación estándar. No obstante, de la misma manera que la media es muy sensible a valores extremos, la desviación estándar es vulnerable a exactamente el mismo problema. Entonces, de la misma manera que la gente a veces usa la mediana como una forma “robusta” de calcular “algo que es como la media”, no es raro usar MAD como método para calcular “algo que es como la desviación estándar”. Desafortunadamente, el valor crudo de MAD no hace esto. Nuestro valor de MAD bruto es 19.5, y nuestra desviación estándar fue 26.07. No obstante, lo que alguna persona inteligente ha demostrado es que, bajo ciertos supuestos 74, se puede multiplicar el valor bruto de MAD por 1.4826 y obtener un número que es directamente comparable a la desviación estándar. Como consecuencia, el valor predeterminado de constant es 1.4826, y así cuando usas el comando mad () sin establecer manualmente un valor, esto es lo que obtienes:
mad( afl.margins ) ## [1] 28.9107Debo señalar, sin embargo, que si quieres usar este valor MAD “corregido” como una versión robusta de la desviación estándar, realmente estás confiando en la suposición de que los datos son (o al menos, “se supone que son” en algún sentido) simétricos y básicamente con forma de curva de campana. Eso realmente no es cierto para nuestros datos afl.margins, así que en este caso no intentaría usar el valor MAD de esta manera.
¿Qué medida usar?
Hemos discutido bastantes medidas de spread (rango, IQR, MAD, varianza y desviación estándar), e insinuamos sus fortalezas y debilidades. Aquí hay un resumen rápido:
- Rango. Te da la difusión completa de los datos. Es muy vulnerable a los valores atípicos, y como consecuencia no se usa a menudo a menos que tengas buenas razones para preocuparte por los extremos en los datos.
- Rango intercuartil. Te dice dónde se encuentra la “mitad media” de los datos. Es bastante robusto y complementa muy bien la mediana. Esto se usa mucho.
- Desviación media absoluta. Te dice qué tan lejos “en promedio” están las observaciones de la media. Es muy interpretable, pero tiene algunas cuestiones menores (no discutidas aquí) que la hacen menos atractiva para los estadísticos que la desviación estándar. Se usa a veces, pero no a menudo.
- Varianza. Te indica la desviación cuadrada promedio de la media. Es matemáticamente elegante, y probablemente sea la forma “correcta” de describir la variación alrededor de la media, pero es completamente ininterpretable porque no usa las mismas unidades que los datos. Casi nunca se usa excepto como herramienta matemática; pero está enterrada “bajo el capó” de un número muy grande de herramientas estadísticas.
- Desviación estándar. Esta es la raíz cuadrada de la varianza. Es bastante elegante matemáticamente, y se expresa en las mismas unidades que los datos por lo que se puede interpretar bastante bien. En situaciones donde la media es la medida de tendencia central, esta es la predeterminada. Esta es, con mucho, la medida de variación más popular.
- Desviación media absoluta. La desviación típica (es decir, mediana) del valor de la mediana. En la forma cruda es simple e interpretable; en la forma corregida es una forma robusta de estimar la desviación estándar, para algunos tipos de conjuntos de datos. No se usa muy a menudo, pero sí se informa a veces.
En definitiva, el IQR y la desviación estándar son fácilmente las dos medidas más comunes utilizadas para reportar la variabilidad de los datos; pero hay situaciones en las que se utilizan las otras. Los he descrito a todos en este libro porque hay una posibilidad justa de que te encuentres con la mayoría de estos en alguna parte.


