5.3: sesgo y curtosis
- Page ID
- 151522
Hay dos estadísticas descriptivas más que a veces verás reportadas en la literatura psicológica, conocidas como sesgo y curtosis. En la práctica, ninguno de los dos se usa tan frecuentemente como las medidas de tendencia central y variabilidad de las que hemos estado hablando. El sesgo es bastante importante, así que lo ves mencionado un poco; pero en realidad nunca he visto la curtosis reportada en un artículo científico hasta la fecha.
## [1] -0.9174977## [1] 0.009023979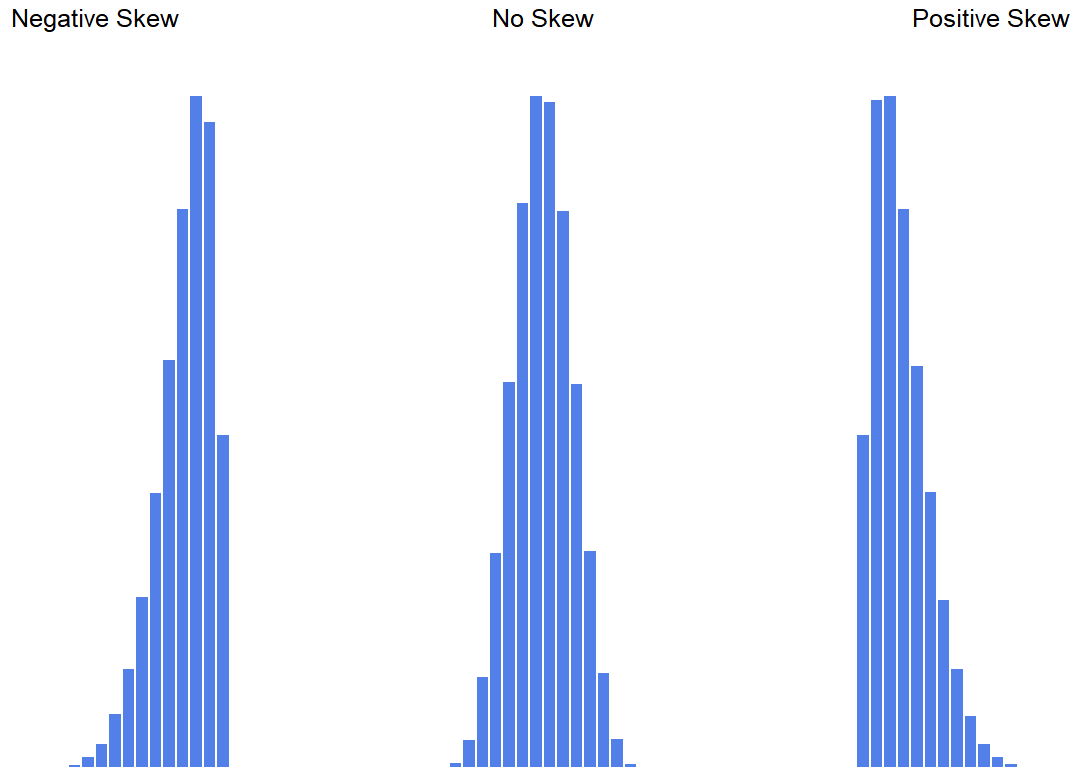
## [1] 0.9250898Ya que es lo más interesante de los dos, comencemos hablando de la asimetría. La asimetría es básicamente una medida de asimetría, y la forma más fácil de explicarla es dibujando algunas imágenes. Como ilustra la Figura 5.4, si los datos tienden a tener muchos valores extremos pequeños (es decir, la cola inferior es “más larga” que la cola superior) y no tantos valores extremadamente grandes (panel izquierdo), entonces decimos que los datos están sesgados negativamente. Por otro lado, si hay valores más extremadamente grandes que los extremadamente pequeños (panel derecho) decimos que los datos están sesgados positivamente. Esa es la idea cualitativa detrás de la asimetría. La fórmula real para la asimetría de un conjunto de datos es la siguiente
\[\text { skewness }(X)=\dfrac{1}{N \hat{\sigma}\ ^{3}} \sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{3} \label{skew}\]
donde N es el número de observaciones,\(\bar{X}\) es la media de la muestra y\(\hat{\sigma}\) es la desviación estándar (la versión “divide por N−1"”, es decir). Quizás de manera más útil, podría ser útil señalar que el paquete psych contiene una función skew () que puedes usar para calcular la asimetría. Entonces, si quisiéramos usar esta función para calcular la asimetría de los datos afl.margins, primero necesitaríamos cargar el paquete
library( psych )que ahora permite usar el siguiente comando:
skew( x = afl.margins ) ## [1] 0.7671555No es sorprendente, resulta que los datos de márgenes ganadores de la AFL están bastante sesgados.
La medida final a la que a veces se hace referencia es la curtosis de un conjunto de datos. En pocas palabras, la curtosis es una medida de la “cola”, o carácter atípico, de los datos. Históricamente, se pensó que esta estadística mide la “puntualidad” o “planitud” de una distribución, pero se ha demostrado que esto es un error de interpretación. Ver Figura 5.5.
## [1] -0.9631805 ## [1] 0.02226287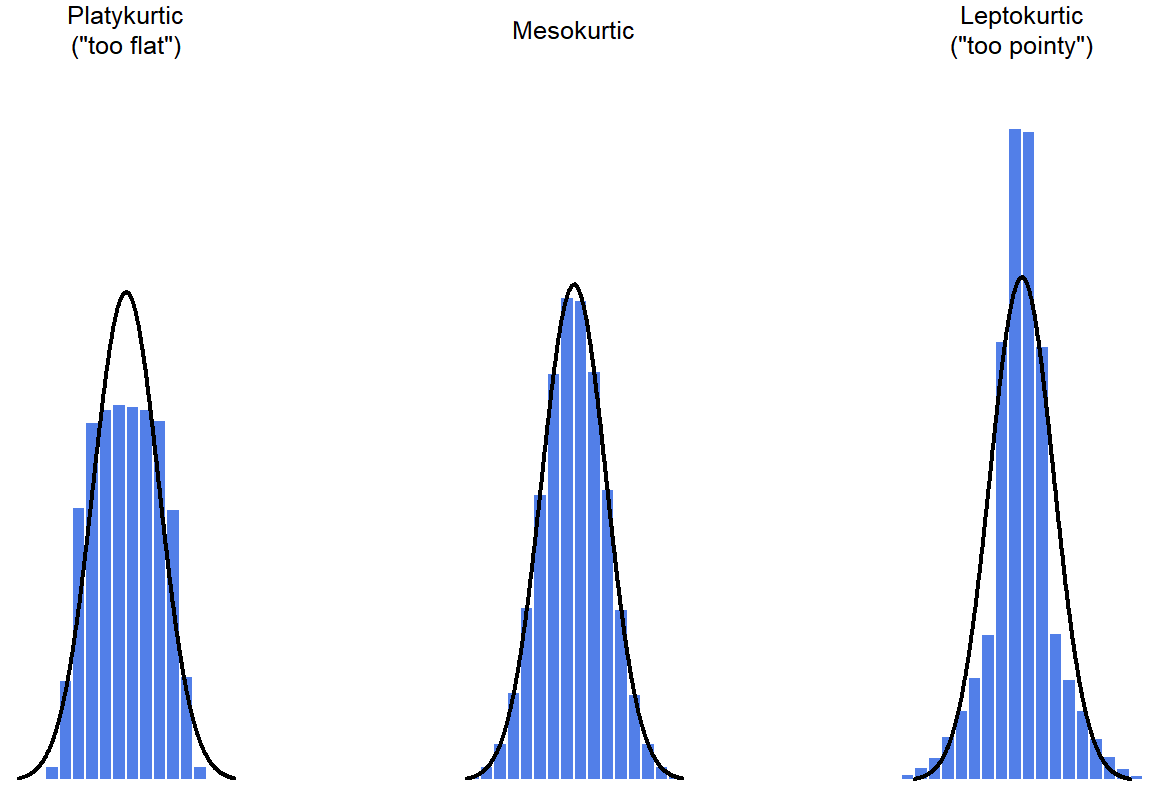
## [1] 1.994329 Por cálculos matemáticos, la “curva normal” (líneas negras) tiene curtosis cero, por lo que se evalúa el carácter atípico de un conjunto de datos en relación con esta curva. En esta Figura, los datos de la izquierda son menos propensos a valores atípicos, por lo que la curtosis es negativa y llamamos a los datos platykurtic. Los datos de la derecha son más propensos a los valores atípicos, por lo que la curtosis es positiva y decimos que los datos son leptoúrticos. Pero los datos en el medio son similares en su carácter atípico, por lo que decimos que es mesocúrtico y tiene curtosis cero. Esto se resume en la siguiente tabla:
| término informal | nombre técnico | valor de curtosis |
|---|---|---|
| lo suficientemente puntiaguda | mesocúrtico | cero |
| demasiado puntiaguda | leptokúrtico | positivo |
| demasiado plano | platykurtic | negativo |
La ecuación para la curtosis es bastante similar en espíritu a las fórmulas que ya hemos visto para la varianza y la asimetría (Ecuación\ ref {sesgo}); excepto que donde la varianza implicaba desviaciones cuadradas y la asimetría implicaba desviaciones en cubos, la curtosis implica elevar las desviaciones a la cuarta potencia: 75
\[\text { kurtosis }(X)=\dfrac{1}{N \hat{\sigma}\ ^{4}} \sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{4}-3\]
El paquete psych tiene una función llamada kurtosi () que puedes usar para calcular la curtosis de tus datos. Por ejemplo, si tuviéramos que hacer esto para los márgenes de AFL,
kurtosi( x = afl.margins )## [1] 0.02962633descubrimos que los datos de los márgenes ganadores de AFL son lo suficientemente puntiagudos.
Colaboradores
- Danielle Navarro (Profesora Asociada (Psicología) en la Universidad de Nueva Gales del Sur)
- Peter H. Westfall (Profesor Paul Whitfield Horn y Profesor James y Marguerite Niver, Universidad Tecnológica de Texas)


