6.6: Gráficas de dispersión
- Page ID
- 151876
Los diagramas de dispersión son una herramienta simple pero efectiva para visualizar datos. Ya hemos visto diagramas de dispersión en este capítulo, al usar la función plot () para dibujar la variable Fibonacci como una colección de puntos (Sección 6.2. No obstante, para los efectos de esta sección tengo en mente una noción ligeramente diferente. En lugar de simplemente trazar una variable, lo que quiero hacer con mi diagrama de dispersión es mostrar la relación entre dos variables, como vimos con las figuras en la sección sobre correlación (Sección 5.7. Es esta última aplicación la que solemos tener en mente cuando usamos el término “scatterplot”. En este tipo de parcela, cada observación corresponde a un punto: la ubicación horizontal del punto traza el valor de la observación en una variable, y la ubicación vertical muestra su valor en la otra variable. En muchas situaciones realmente no tienes opiniones claras sobre cuál es la relación causal (por ejemplo, A causa B, o B causa A, o alguna otra variable C controla tanto A como B). Si ese es el caso, realmente no importa qué variable trazar en el eje x y cuál trazar en el eje y. Sin embargo, en muchas situaciones sí tienes una idea bastante fuerte de qué variable crees que es más probable que sea causal, o al menos tienes algunas sospechas en esa dirección. Si es así, entonces es convencional trazar la variable causa en el eje x, y la variable de efecto en el eje y. Con eso en mente, veamos cómo dibujar diagramas de dispersión en R, usando el mismo conjunto de datos de paternidad (es decir, Parenthood.rData) que utilicé al introducir la idea de correlaciones.
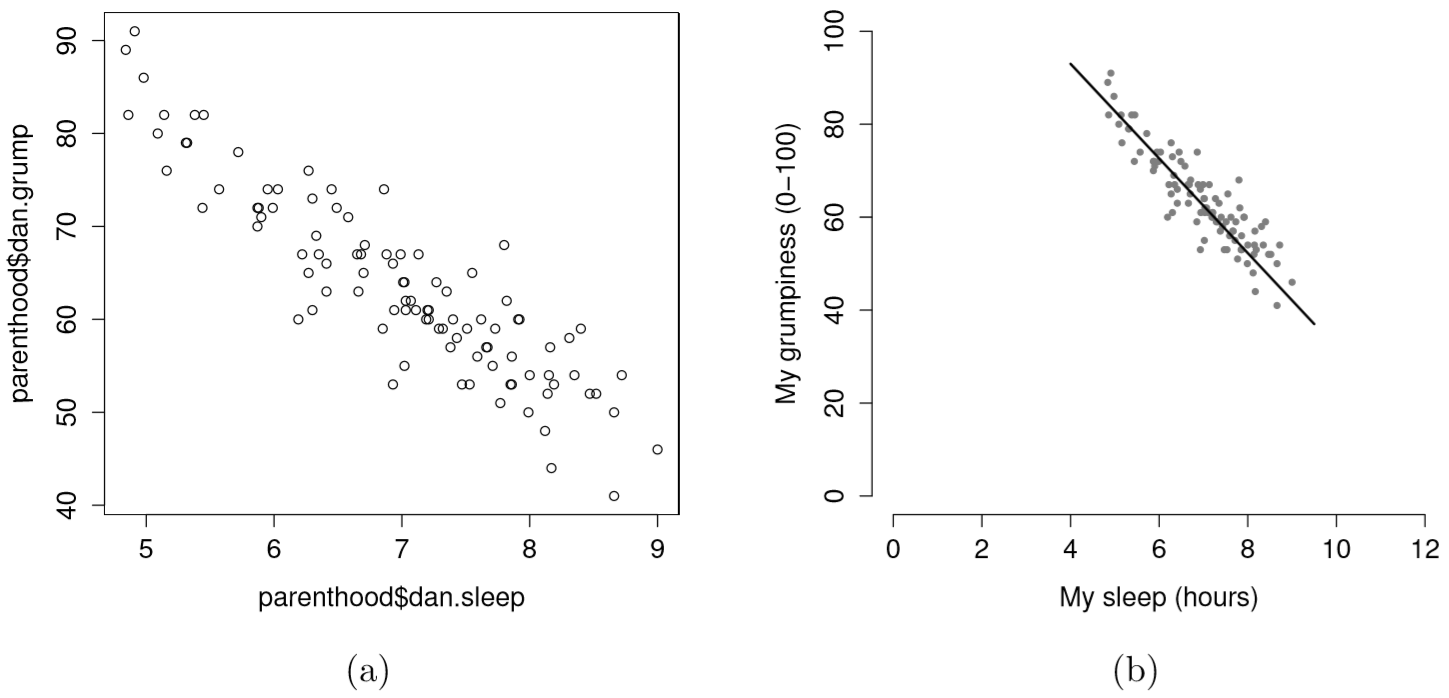
Supongamos que mi objetivo es dibujar un diagrama de dispersión que muestre la relación entre la cantidad de sueño que obtengo (dan.sleep) y lo gruñón que estoy al día siguiente (dan.gruñón). Como cabría esperar dado nuestro uso anterior de plot () para mostrar los datos de Fibonacci, la función que usamos es la función plot (), pero debido a que es una función genérica, la función plot.default () sigue realizando el trabajo duro. En cualquier caso, hay dos formas distintas en las que podemos conseguir la trama que buscamos. La primera forma es especificar el nombre de la variable que se va a trazar en el eje x y la variable a trazar en el eje y. Cuando lo hacemos de esta manera, el comando se ve así:
plot( x = parenthood$dan.sleep, # data on the x-axis
y = parenthood$dan.grump # data on the y-axis
) 
La segunda forma de hacerlo es usar un formato de “fórmula y marco de datos”, pero voy a evitar usarlo. 99 Por ahora, sigamos con la versión x e y. Si hacemos esto, el resultado es la gráfica de dispersión muy básica que se muestra en la Figura 6.19. Esto sirve bastante bien, pero hay algunas personalizaciones que probablemente queramos hacer para que este funcione correctamente. Como de costumbre, queremos agregar algunas etiquetas, pero hay algunas otras cosas que quizás también queramos hacer. En primer lugar, a veces es útil reescalar las parcelas. En la Figura 6.19 R ha seleccionado las escalas para que los datos caigan pulcramente en el medio. Pero, en este caso, resulta que sabemos que la medida de maldad cae en una escala de 0 a 100, y las horas dormidas caen en una escala natural entre 0 horas y aproximadamente 12 horas más o menos (las más largas que puedo dormir en la vida real). Entonces el comando que podría usar para dibujar esto es:
plot( x = parenthood$dan.sleep, # data on the x-axis
y = parenthood$dan.grump, # data on the y-axis
xlab = "My sleep (hours)", # x-axis label
ylab = "My grumpiness (0-100)", # y-axis label
xlim = c(0,12), # scale the x-axis
ylim = c(0,100), # scale the y-axis
pch = 20, # change the plot type
col = "gray50", # dim the dots slightly
frame.plot = FALSE # don't draw a box
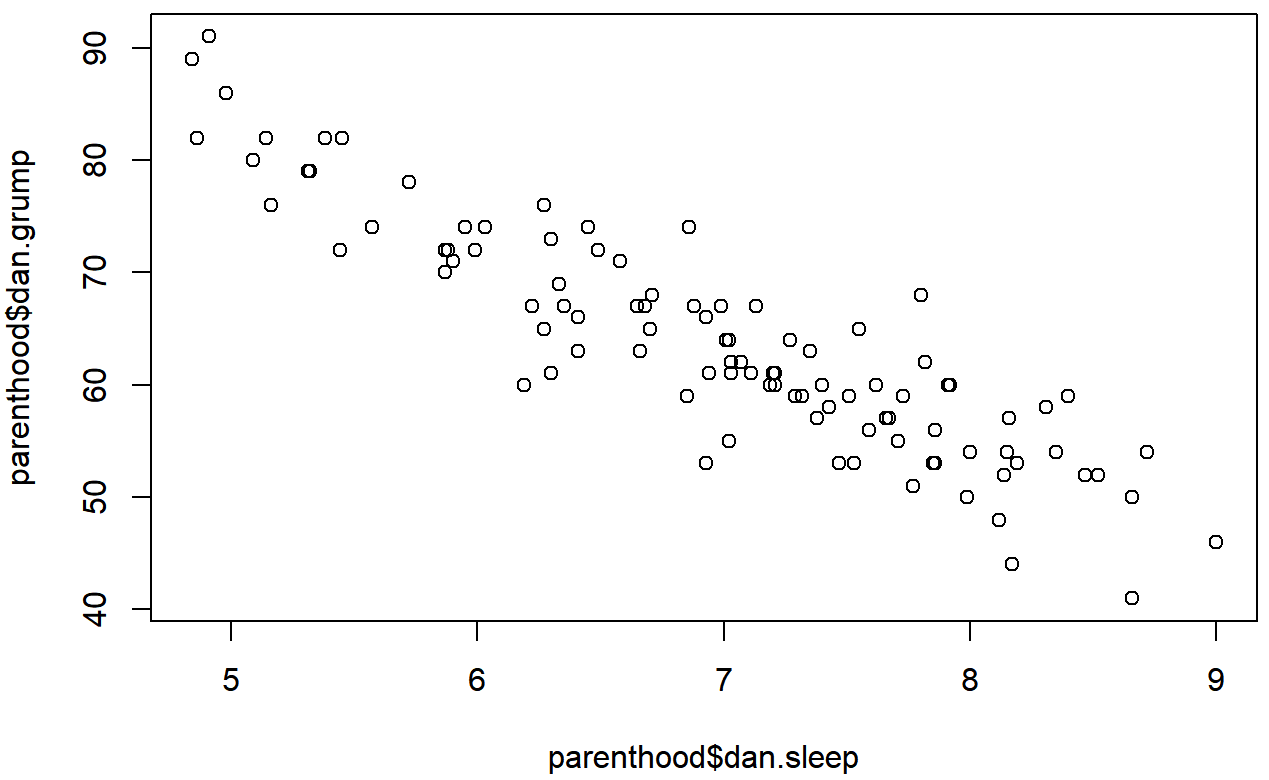
)Este comando produce la gráfica de dispersión en la Figura?? , o al menos muy cerca. Lo que no hace es trazar la línea a través de la mitad de los puntos. A veces puede ser muy útil hacer esto, y puedo hacerlo usando lines (), que es una función de plotting de bajo nivel. Mejor aún, los argumentos que necesito especificar son prácticamente los mismos que uso al llamar a la función plot (). Es decir, supongamos que quiero trazar una línea que vaya del punto (4,93) al punto (9.5,37). Entonces las ubicaciones x pueden ser especificadas por el vector c (4,9.5) y las ubicaciones y corresponden al vector c (93,37). En otras palabras, utilizo este comando:
plot( x = parenthood$dan.sleep, # data on the x-axis
y = parenthood$dan.grump, # data on the y-axis
xlab = "My sleep (hours)", # x-axis label
ylab = "My grumpiness (0-100)", # y-axis label
xlim = c(0,12), # scale the x-axis
ylim = c(0,100), # scale the y-axis
pch = 20, # change the plot type
col = "gray50", # dim the dots slightly
frame.plot = FALSE # don't draw a box
)
lines( x = c(4,9.5), # the horizontal locations
y = c(93,37), # the vertical locations
lwd = 2 # line width
)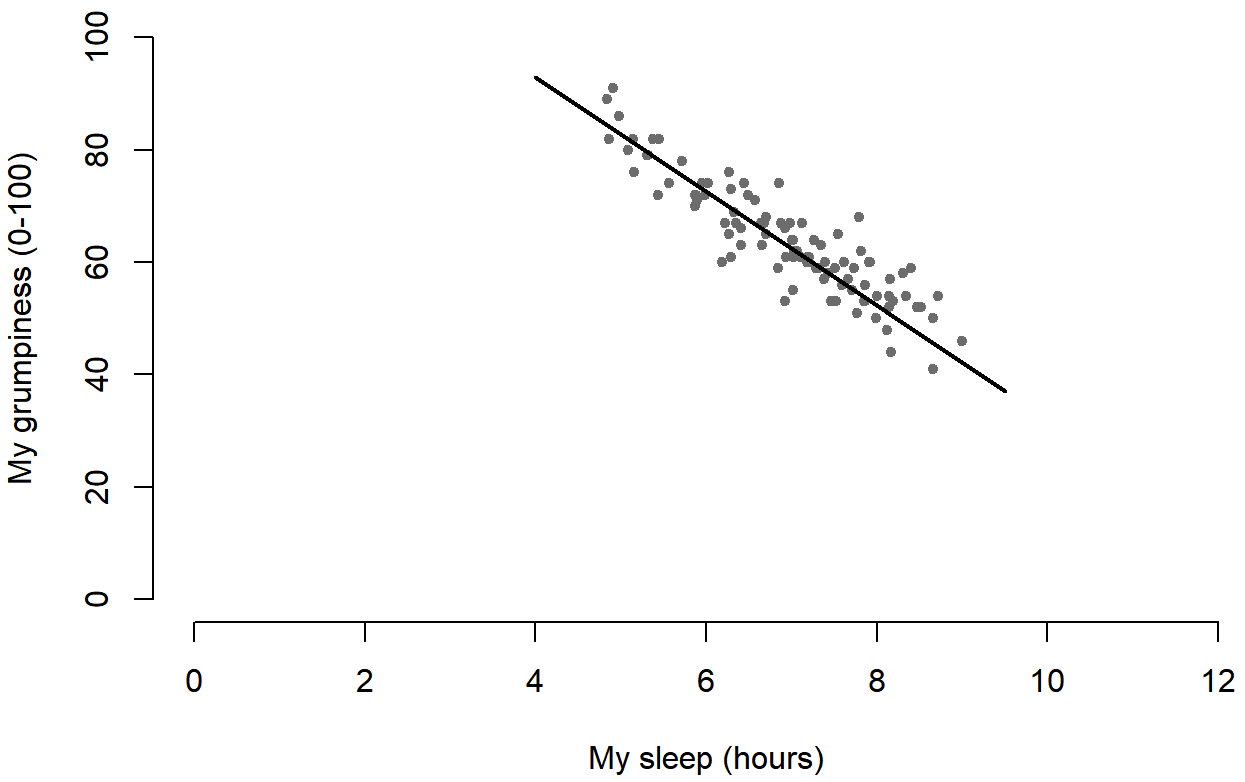
Y cuando lo hago, R traza la línea sobre la parte superior de la trama que dibujé usando el comando anterior. En la mayoría de las situaciones de análisis de datos realistas, absolutamente no quieres adivinar a dónde va la línea a través de los puntos, ya que hay alrededor de mil millones de formas diferentes en las que puedes conseguir que R haga un mejor trabajo. Sin embargo, al menos ilustra la idea básica.
Una posibilidad, si quieres que R dibuje líneas limpias agradables a través de los datos por ti, es usar la función scatterplot () en el paquete del auto. Antes de poder usar scatterplot () necesitamos cargar el paquete:
> library( car )Una vez hecho esto, ya podemos usar la función. El comando que necesitamos es este:
> scatterplot( dan.grump ~ dan.sleep,
+ data = parenthood,
+ smooth = FALSE
+ )
## Loading required package: carData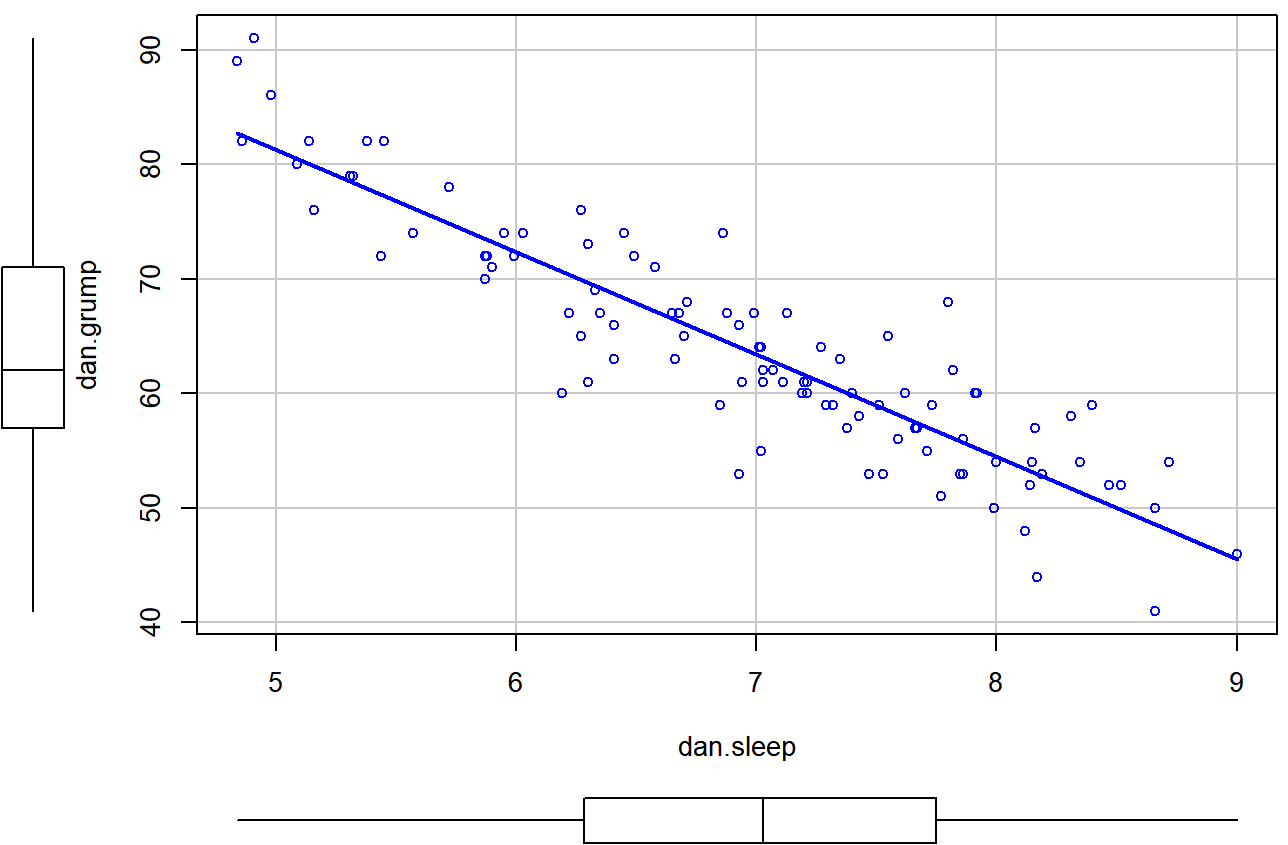
scatterplot () en el paquete del automóvil.Los dos primeros argumentos deberían ser familiares: la primera entrada es una fórmula dan.grump ~ dan.sleep diciéndole a R qué variables trazar, 100 y el segundo especifica un marco de datos. El tercer argumento suave que he establecido en FALSE para evitar que la función scatterplot () dibuje una elegante línea de tendencia “suavizada” (ya que es un poco confuso para los principiantes). La gráfica de dispersión en sí se muestra en la Figura 6.20. Como puede ver, no solo se dibuja la gráfica de dispersión, sino que también se dibujan diagramas de caja para cada una de las dos variables, así como una línea simple de mejor ajuste que muestra la relación entre las dos variables.
Opciones más elaboradas
Muchas veces te encuentras queriendo mirar las relaciones entre varias variables a la vez. Una herramienta útil para hacerlo es producir una matriz de diagrama de dispersión, análoga a la matriz de correlación.
> cor( x = parenthood ) # calculate correlation matrix
dan.sleep baby.sleep dan.grump day
dan.sleep 1.00000000 0.62794934 -0.90338404 -0.09840768
baby.sleep 0.62794934 1.00000000 -0.56596373 -0.01043394
dan.grump -0.90338404 -0.56596373 1.00000000 0.07647926
day -0.09840768 -0.01043394 0.07647926 1.00000000Podemos obtener una matriz de diagrama de dispersión correspondiente usando la función pairs (): 101
pairs( x = parenthood ) # draw corresponding scatterplot matrix 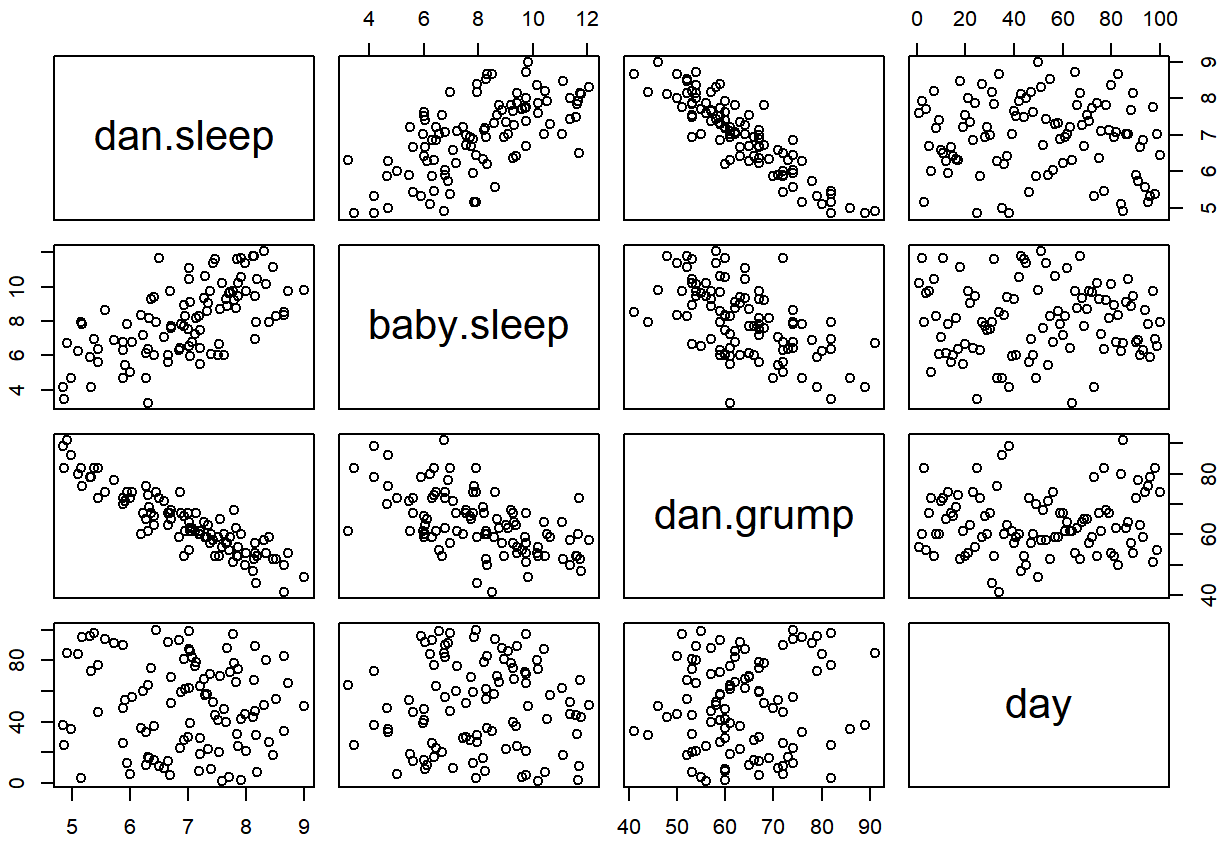
La salida del comando pairs () se muestra en la Figura?? . Una forma alternativa de llamar a la función pairs (), que puede ser útil en algunas situaciones, es especificar las variables a incluir usando una fórmula unilateral. Por ejemplo, este
> pairs( formula = ~ dan.sleep + baby.sleep + dan.grump,
+ data = parenthood
+ )produciría una matriz de 3×3 scatterplot que solo compara dan.sleep, dan.grump y baby.sleep. Obviamente, la primera versión es mucho más fácil, pero hay casos en los que realmente solo quieres mirar algunas de las variables, así que es agradable usar la interfaz de fórmula.


