9.2: ¿Qué significa probabilidad?
- Page ID
- 151620
Empecemos con la primera de estas preguntas. ¿Qué es “probabilidad”? Puede parecerle sorprendente, pero mientras los estadísticos y matemáticos (en su mayoría) coinciden en cuáles son las reglas de probabilidad, hay mucho menos consenso sobre lo que realmente significa la palabra. Parece raro porque todos estamos muy cómodos usando palabras como “azar”, “probable”, “posible” y “probable”, y no parece que deba ser una pregunta muy difícil de responder. Si tuvieras que explicarle “probabilidad” a un niño de cinco años, podrías hacer un trabajo bastante bueno. Pero si alguna vez has tenido esa experiencia en la vida real, podrías alejarte de la conversación sintiendo que no lo hiciste bien, y eso (como muchos conceptos cotidianos) resulta que realmente no sabes de qué se trata.
Entonces voy a intentarlo. Supongamos que quiero apostar por un partido de futbol entre dos equipos de robots, Arduino Arsenal y C Milan. Después de pensarlo, decido que hay un 80% de probabilidad de que Arduino Arsenal gane. ¿Qué quiero decir con eso? Aquí hay tres posibilidades...
- Son equipos de robots, así que puedo hacerlos jugar una y otra vez, y si lo hiciera, Arduino Arsenal ganaría 8 de cada 10 juegos en promedio.
- Para cualquier juego dado, solo estaría de acuerdo en que apostar en este juego solo es “justo” si una apuesta de $1 en C Milan da una recompensa de $5 (es decir, me devuelvo $1 más una recompensa de $4 por ser correcta), al igual que una apuesta de $4 en Arduino Arsenal (es decir, mi apuesta de $4 más una recompensa de $1).
- Mi subjetiva “creencia” o “confianza” en una victoria de Arduino Arsenal es cuatro veces más fuerte que mi creencia en una victoria del C Milan.
Cada uno de estos parece sensato. Sin embargo no son idénticos, y no todos los estadísticos los respaldarían a todos. La razón es que existen diferentes ideologías estadísticas (¡sí, de verdad!) y dependiendo a cuál te suscribas, podrías decir que algunas de esas declaraciones carecen de sentido o son irrelevantes. En esta sección, doy una breve introducción a los dos enfoques principales que existen en la literatura. Estos no son de ninguna manera los únicos enfoques, sino que son los dos grandes.
vista frecuentista
El primero de los dos enfoques principales de probabilidad, y el más dominante en estadística, se conoce como la visión frecuentista, y define la probabilidad como una frecuencia de largo plazo. Supongamos que íbamos a intentar voltear una moneda justa, una y otra vez. Por definición, se trata de una moneda que tiene P (H) =0.5. ¿Qué podríamos observar? Una posibilidad es que los primeros 20 volteos se vean así:
T,H,H,H,H,T,T,H,H,H,H,T,H,H,T,T,T,T,T,H| número.de.flips | número.de.cabezas | proporción |
|---|---|---|
| 1 | 0 | 0.00 |
| 2 | 1 | 0.50 |
| 3 | 2 | 0.67 |
| 4 | 3 | 0.75 |
| 5 | 4 | 0.80 |
| 6 | 4 | 0.67 |
| 7 | 4 | 0.57 |
| 8 | 5 | 0.63 |
| 9 | 6 | 0.67 |
| 10 | 7 | 0.70 |
| 11 | 8 | 0.73 |
| 12 | 8 | 0.67 |
| 13 | 9 | 0.69 |
| 14 | 10 | 0.71 |
| 15 | 10 | 0.67 |
| 16 | 10 | 0.63 |
| 17 | 10 | 0.59 |
| 18 | 10 | 0.56 |
| 19 | 10 | 0.53 |
| 20 | 11 | 0.55 |
Observe que al inicio de la secuencia, la proporción de cabezas fluctúa salvajemente, comenzando en .00 y subiendo tan alto como .80. Más tarde, uno tiene la impresión de que amortigua un poco, con más y más de los valores en realidad muy cerca de la respuesta “correcta” de .50. Esta es la definición frecuentista de probabilidad en pocas palabras: voltear una moneda justa una y otra vez, y a medida que N crece (se acerca al infinito, denotado N→∞), la proporción de cabezas convergerá al 50%. Hay algunos tecnicismos sutiles que preocupan a los matemáticos, pero cualitativamente hablando, así es como los frecuentistas definen la probabilidad. Desafortunadamente, no tengo un número infinito de monedas, o la paciencia infinita que se requiere para voltear una moneda un número infinito de veces. Sin embargo, sí tengo una computadora, y las computadoras sobresalen en tareas repetitivas sin sentido. Entonces le pedí a mi computadora que simulara voltear una moneda 1000 veces, y luego dibujé una imagen de lo que sucede con la proporción N H/N a medida que aumenta N. En realidad, lo hice cuatro veces, sólo para asegurarme de que no era una suerte. Los resultados se muestran en la Figura 9.1. Como puede ver, la proporción de cabezas observadas finalmente deja de fluctuar, y se establece; cuando lo hace, el número en el que finalmente se asienta es la verdadera probabilidad de cabezas.
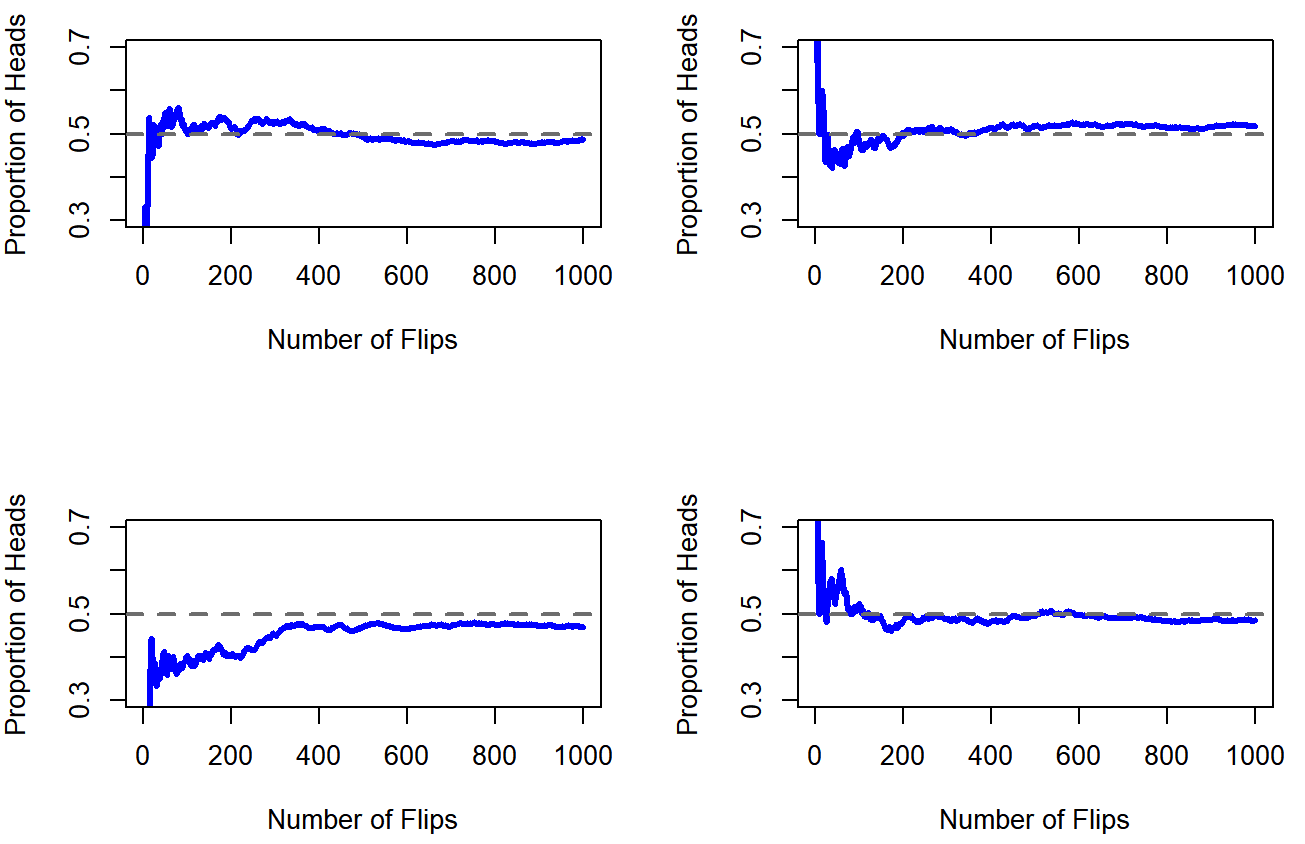
La definición frecuentista de probabilidad tiene algunas características deseables. En primer lugar, es objetivo: la probabilidad de un evento está necesariamente fundamentada en el mundo. La única manera en que las declaraciones de probabilidad pueden tener sentido es si se refieren a (una secuencia de) eventos que ocurren en el universo físico. 142 En segundo lugar, es inequívoco: dos personas cualesquiera que vean desarrollarse la misma secuencia de eventos, tratando de calcular la probabilidad de un evento, inevitablemente deben llegar a la misma respuesta. Sin embargo, también presenta características indeseables. En primer lugar, las secuencias infinitas no existen en el mundo físico. Supongamos que recogiste una moneda de tu bolsillo y empezaste a voltearla. Cada vez que aterriza, impacta en el suelo. Cada impacto desgasta un poco la moneda; eventualmente, la moneda será destruida. Entonces, uno podría preguntarse si realmente tiene sentido pretender que una secuencia “infinita” de volteos de monedas es incluso un concepto significativo, o uno objetivo. No podemos decir que una “secuencia infinita” de eventos sea algo real en el universo físico, porque el universo físico no permite nada infinito. Más en serio, la definición frecuencista tiene un alcance estrecho. Hay muchas cosas por ahí a las que los seres humanos están felices de asignar probabilidad en el lenguaje cotidiano, pero no pueden (ni siquiera en teoría) mapearse en una secuencia hipotética de eventos. Por ejemplo, si un meteorólogo sale por televisión y dice, “la probabilidad de lluvia en Adelaida el 2 de noviembre de 2048 es del 60%” nosotros los humanos estamos felices de aceptar esto. Pero no está claro cómo definir esto en términos frecuentistas. Sólo hay una ciudad de Adelaida, y sólo el 2 de noviembre de 2048. Aquí no hay una secuencia infinita de eventos, solo una cosa única. La probabilidad frecuentista realmente nos prohíbe hacer declaraciones de probabilidad sobre un solo evento. Desde la perspectiva frecuentista, o lloverá mañana o no lo hará; no hay “probabilidad” que se apegue a un solo evento no repetible. Ahora bien, habría que decir que hay algunos trucos muy inteligentes que los frecuentistas pueden utilizar para sortear esto. Una posibilidad es que lo que quiere decir el meteorólogo es algo así: “Hay una categoría de días para los que predigo un 60% de probabilidad de lluvia; si miramos sólo a través de esos días para los que hago esta predicción, entonces en el 60% de esos días realmente va a llover”. Es muy raro y contrario a la intuición pensarlo de esta manera, pero sí ves que los frecuentistas hacen esto a veces. Y saldrá más adelante en este libro (ver Sección 10.5).
Vista bayesiana
La visión bayesiana de la probabilidad se suele llamar la visión subjetivista, y es una visión minoritaria entre los estadísticos, pero que ha ido ganando terreno de manera constante durante las últimas décadas. Hay muchos sabores del bayesianismo, lo que dificulta decir exactamente cuál es “la” visión bayesiana. La forma más común de pensar sobre la probabilidad subjetiva es definir la probabilidad de un evento como el grado de creencia que un agente inteligente y racional asigna a esa verdad de ese evento. Desde esa perspectiva, las probabilidades no existen en el mundo, sino en los pensamientos y suposiciones de las personas y otros seres inteligentes. No obstante, para que este enfoque funcione, necesitamos alguna forma de operacionalizar el “grado de creencia”. Una forma de hacerlo es formalizarlo en términos de “juego racional”, aunque hay muchas otras formas. Supongamos que creo que hay un 60% de probabilidad de lluvia mañana. Si alguien me ofrece una apuesta: si llueve mañana, entonces gano 5 dólares, pero si no llueve entonces pierdo 5 dólares. Claramente, desde mi perspectiva, esta es una apuesta bastante buena. Por otro lado, si pienso que la probabilidad de lluvia es solo del 40%, entonces es una mala apuesta para tomar. Así, podemos operacionalizar la noción de una “probabilidad subjetiva” en términos de qué apuestas estoy dispuesto a aceptar.
¿Cuáles son las ventajas y desventajas del enfoque bayesiano? La principal ventaja es que permite asignar probabilidades a cualquier evento que desee. No es necesario que te limites a aquellos eventos que son repetibles. La principal desventaja (para muchas personas) es que no podemos ser puramente objetivos —especificar una probabilidad requiere que especifiquemos una entidad que tenga el grado de creencia relevante. Esta entidad podría ser un humano, un extraterrestre, un robot, o incluso un estadístico, pero tiene que haber un agente inteligente por ahí que crea en las cosas. Para mucha gente esto es incómodo: parece hacer que la probabilidad sea arbitraria. Si bien el enfoque bayesiano sí requiere que el agente en cuestión sea racional (es decir, obedecer las reglas de probabilidad), sí permite que cada uno tenga sus propias creencias; puedo creer que la moneda es justa y no es necesario, aunque ambos seamos racionales. La vista frecuentista no permite que dos observadores atribuyan probabilidades diferentes al mismo evento: cuando eso sucede, entonces al menos uno de ellos debe estar equivocado. El punto de vista bayesiano no impide que esto ocurra. Dos observadores con diferentes conocimientos de fondo pueden tener legítimamente diferentes creencias sobre un mismo evento. En definitiva, donde la visión frecuentista a veces se considera demasiado estrecha (prohíbe muchas cosas a las que queremos asignar probabilidades), a veces se piensa que la visión bayesiana es demasiado amplia (permite demasiadas diferencias entre observadores).
¿Cuál es la diferencia? ¿Y quién tiene razón?
Ahora que has visto cada una de estas dos vistas de forma independiente, es útil asegurarte de que puedes comparar las dos. Volver al hipotético juego de fútbol robot al inicio de la sección. ¿Qué opinas que dirían un frecuentista y un bayesiano sobre estas tres afirmaciones? ¿Qué afirmación diría un frecuentista es la definición correcta de probabilidad? ¿Cuál haría un bayesiano? ¿Algunas de estas afirmaciones carecerían de sentido para un frecuentista o un bayesiano? Si has entendido las dos perspectivas, deberías tener algún sentido de cómo responder esas preguntas.
Bien, suponiendo que entiendas lo diferente, tal vez te estés preguntando cuál de ellos es correcto? Honestamente, no sé que haya una respuesta correcta. Por lo que puedo decir no hay nada matemáticamente incorrecto en la forma en que los frecuentistas piensan sobre secuencias de eventos, y no hay nada matemáticamente incorrecto en la forma en que los bayesianos definen las creencias de un agente racional. De hecho, cuando profundizas en los detalles, los bayesianos y los frecuentistas están de acuerdo en muchas cosas. Muchos métodos frecuentistas llevan a decisiones que los bayesianos coinciden en que tomaría un agente racional. Muchos métodos bayesianos tienen muy buenas propiedades frecuentistas.
En su mayor parte, soy pragmático así que utilizaré cualquier método estadístico en el que confíe. Resulta que eso me hace preferir los métodos bayesianos, por razones que voy a explicar hacia el final del libro, pero no me opongo fundamentalmente a los métodos frecuentistas. No todos están tan relajados. Por ejemplo, consideremos a Sir Ronald Fisher, una de las figuras imponentes de las estadísticas del siglo XX y un vehemente oponente a todas las cosas bayesianas, cuyo trabajo sobre los fundamentos matemáticos de la estadística se refirió a la probabilidad bayesiana como “una selva impenetrable [que] detenciones avanzan hacia la precisión de conceptos estadísticos” Fisher (1922b). O el psicólogo Paul Meehl, quien sugiere que apoyarse en métodos frecuentistas podría convertirte en “un rastrillo intelectual potente pero estéril que deja en su alegre camino un largo tren de doncellas violadas pero ninguna descendencia científica viable” Meehl (1967). La historia de las estadísticas, como podrías reunir, no está desprovista de entretenimiento.
En cualquier caso, si bien personalmente prefiero la visión bayesiana, la mayoría de los análisis estadísticos se basan en el enfoque frecuentista. Mi razonamiento es pragmático: el objetivo de este libro es cubrir aproximadamente el mismo territorio que una clase típica de estadísticas de licenciatura en psicología, y si quieres entender las herramientas estadísticas utilizadas por la mayoría de los psicólogos, necesitarás una buena comprensión de los métodos frecuentistas. Te prometo que esto no es esfuerzo desperdiciado. Incluso si terminas queriendo cambiar a la perspectiva bayesiana, realmente deberías leer al menos un libro sobre la visión frecuentista “ortodoxa”. Y dado que R es el lenguaje estadístico más utilizado para los bayesianos, también podrías leer un libro que usa R. Además, no voy a ignorar por completo la perspectiva bayesiana. De vez en cuando agregaré algunos comentarios desde el punto de vista bayesiano, y volveré a examinar el tema con más profundidad en el Capítulo 17.


