9.3: Teoría Básica de Probabilidad
- Page ID
- 151636
A pesar de los argumentos ideológicos entre bayesianos y frecuencistas, resulta que la mayoría de las personas coinciden en las reglas que las probabilidades deben obedecer. Hay muchas maneras diferentes de llegar a estas reglas. El enfoque más utilizado se basa en el trabajo de Andrey Kolmogorov, uno de los grandes matemáticos soviéticos del siglo XX. No voy a entrar en muchos detalles, pero voy a tratar de darle un poco de idea de cómo funciona. Y para poder hacerlo voy a tener que hablar de mis pantalones.
Introducción de distribuciones de probabilidad
Una de las verdades inquietantes de mi vida es que solo tengo 5 pares de pantalones: tres pares de jeans, la mitad inferior de un traje y un par de pantalones de chándal. Aún más triste, les he dado nombres: los llamo X 1, X 2, X 3, X 4 y X 5. De verdad lo hago: por eso me llaman Señor Imaginativo. Ahora, en un día cualquiera, elijo exactamente uno de par de pantalones para usar. Ni siquiera soy tan estúpida como para tratar de ponerme dos pares de pantalones, y gracias a años de entrenamiento nunca salgo a la calle sin usar más pantalón. Si tuviera que describir esta situación usando el lenguaje de la teoría de la probabilidad, me referiría a cada par de pantalones (es decir, cada X) como un evento elemental. La característica clave de los eventos elementales es que cada vez que hacemos una observación (por ejemplo, cada vez que me pongo un par de pantalones), entonces el resultado será uno y solo uno de estos eventos. Como dije, en estos días siempre llevo exactamente un par de pantalones, así que mis pantalones satisfacen esta restricción. Del mismo modo, el conjunto de todos los eventos posibles se denomina espacio de muestra. Concedido, algunas personas lo llamarían un “vestuario”, pero eso es porque se niegan a pensar en mis pantalones en términos probabilísticos. Triste.
Bien, ahora que tenemos un espacio de muestra (un armario), que se construye a partir de muchos eventos elementales posibles (pantalones), lo que queremos hacer es asignar una probabilidad de uno de estos eventos elementales. Para un evento X, la probabilidad de ese evento P (X) es un número que se encuentra entre 0 y 1. Cuanto mayor sea el valor de P (X), más probable es que ocurra el evento. Entonces, por ejemplo, si P (X) =0, significa que el evento X es imposible (es decir, nunca me pongo esos pantalones). Por otro lado, si P (X) =1 significa que el evento X es seguro que ocurrirá (es decir, siempre uso esos pantalones). Para valores de probabilidad en el medio, significa que a veces llevo esos pantalones. Por ejemplo, si P (X) =0.5 significa que llevo esos pantalones la mitad del tiempo.
En este punto, ya casi terminamos. Lo último que debemos reconocer es que “siempre pasa algo”. Cada vez que me pongo pantalones, realmente termino usando pantalones (loco, ¿verdad?). Lo que significa esta afirmación algo trillada, en términos probabilísticos, es que las probabilidades de los eventos elementales tienen que sumar hasta 1. Esto se conoce como la ley de la probabilidad total, no es que a ninguno de nosotros realmente nos importe. Más importante aún, si se cumplen estos requisitos, entonces lo que tenemos es una distribución de probabilidad. Por ejemplo, este es un ejemplo de una distribución de probabilidad
| CUA.PANTALONES | Azul.Jeans | Gris.jeans | Negro.Jeans | Negro.Traje | Blue.Chándal |
|---|---|---|---|---|---|
| Etiqueta | X 1 | X 2 | X 3 | X 4 | X 5 |
| Probabilidad | P (X 1) =.5 | P (X 2) =.3 | P (X 3) =.1 | P (X 4) =0 | P (X 5) =.1 |
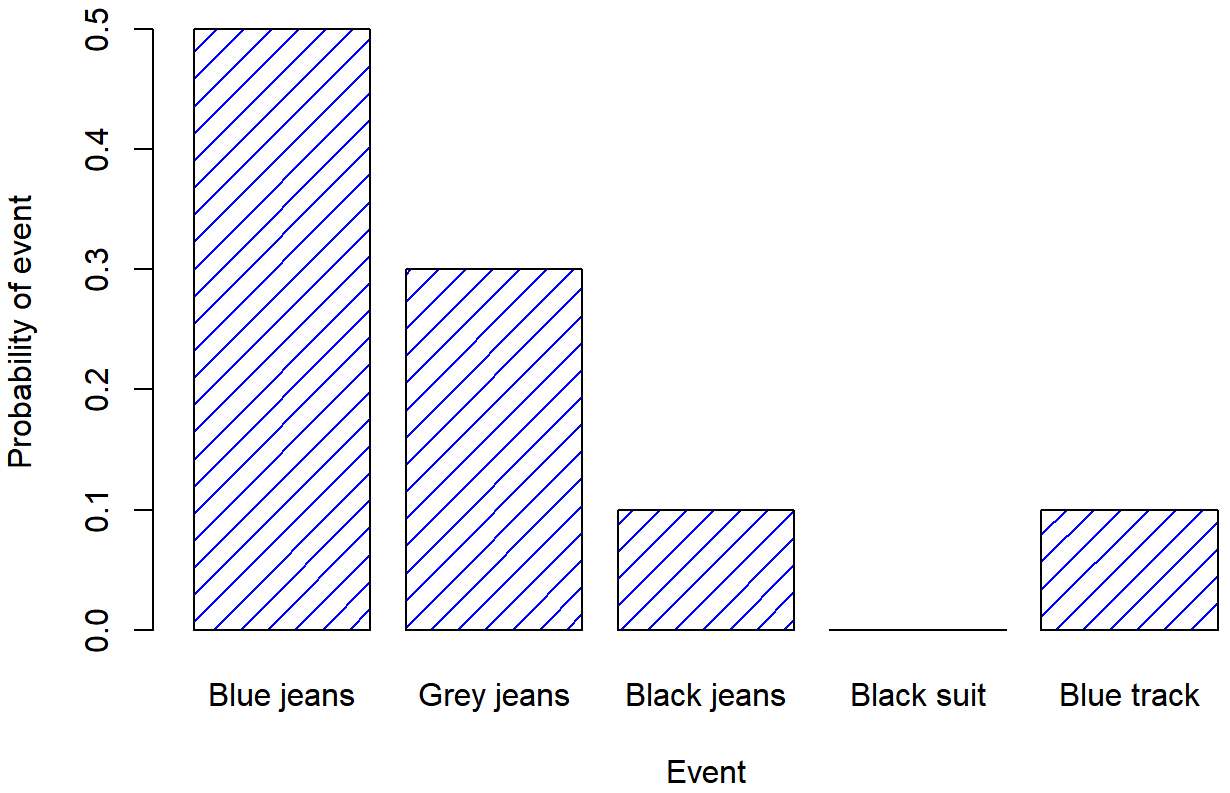
Cada uno de los eventos tiene una probabilidad que se encuentra entre 0 y 1, y si sumamos la probabilidad de todos los eventos, suman a 1. Impresionante. Incluso podemos dibujar un bonito gráfico de barras (ver Sección 6.7) para visualizar esta distribución, como se muestra en la Figura?? . Y en este punto, todos hemos logrado algo. Has aprendido lo que es una distribución de probabilidad, y finalmente he logrado encontrar la manera de crear una gráfica que se centre completamente en mis pantalones. ¡Todos ganan!
La única otra cosa que necesito señalar es que la teoría de probabilidad permite hablar tanto de eventos no elementales como de elementales. La forma más fácil de ilustrar el concepto es con un ejemplo. En el ejemplo de los pantalones, es perfectamente legítimo referirse a la probabilidad de que use jeans. En este escenario, el evento de “Dan lleva jeans” que se dice que ocurrió siempre y cuando el evento elemental que realmente ocurrió sea uno de los apropiados; en este caso “blue jeans”, “black jeans” o “grey jeans”. En términos matemáticos, definimos el evento “jeans” E para que corresponda al conjunto de eventos elementales (X 1, X 2, X 3). Si ocurre alguno de estos eventos elementales, entonces también se dice que E ocurrió. Habiendo decidido anotar la definición de la E de esta manera, es bastante sencillo afirmar cuál es la probabilidad P (E): simplemente sumamos todo. En este caso particular
P (E) =P (X 1) +P (X 2) +P (X 3)
y, dado que las probabilidades de los vaqueros azules, grises y negros respectivamente son .5, .3 y .1, la probabilidad de que use jeans es igual a .9.
En este punto podrías estar pensando que todo esto es terriblemente obvio y simple y tendrías razón. Todo lo que realmente hemos hecho es envolver algunas matemáticas básicas alrededor de algunas intuiciones de sentido común. Sin embargo, a partir de estos simples comienzos es posible construir algunas herramientas matemáticas extremadamente poderosas. Definitivamente no voy a entrar en los detalles en este libro, pero lo que voy a hacer es enumerar —en la Tabla 9.1— algunas de las otras reglas que las probabilidades satisfacen. Estas reglas pueden derivarse de los simples supuestos que he esbozado anteriormente, pero como en realidad no usamos estas reglas para nada en este libro, no lo haré aquí.
Cuadro 9.1: Algunas reglas básicas que las probabilidades deben satisfacer. Realmente no necesitas conocer estas reglas para entender los análisis de los que hablaremos más adelante en el libro, pero son importantes si quieres entender un poco más a fondo la teoría de la probabilidad.
| Inglés | Notación | NANA | Fórmula |
|---|---|---|---|
| No A | P (¬A) | = | 1−P (A) |
| A o B | P (AB) | = | P (A) +P (B) −P (AB) |
| A y B | P (AB) | = | P (A|B) P (B) |


