9.5: La distribución normal
- Page ID
- 151652
Si bien la distribución binomial es conceptualmente la distribución más simple de entender, no es la más importante. Ese honor particular va a la distribución normal, a la que también se le conoce como “la curva de campana” o una “distribución gaussiana”. Se describe una distribución normal utilizando dos parámetros, la media de la distribución μ y la desviación estándar de la distribución σ. La notación que a veces usamos para decir que una variable X se distribuye normalmente es la siguiente:
X~Normal (μ, σ)
Por supuesto, eso es sólo notación. No nos dice nada interesante sobre la distribución normal en sí misma. Como fue el caso de la distribución binomial, he incluido la fórmula para la distribución normal en este libro, porque creo que es lo suficientemente importante que todos los que aprenden estadísticas deberían al menos mirarlo, pero como este es un texto introductorio no quiero centrarme en él, así que lo he escondido en Cuadro 9.2. Del mismo modo, las funciones R para la distribución normal son dnorm (), pnorm (), qnorm () y rnorm (). Sin embargo, se comportan prácticamente de la misma manera que las funciones correspondientes para la distribución binomial, así que no hay mucho que necesites saber. Lo único que debo señalar es que los nombres de los argumentos para los parámetros son mean y sd. En casi todos los demás aspectos, no hay nada más que agregar.
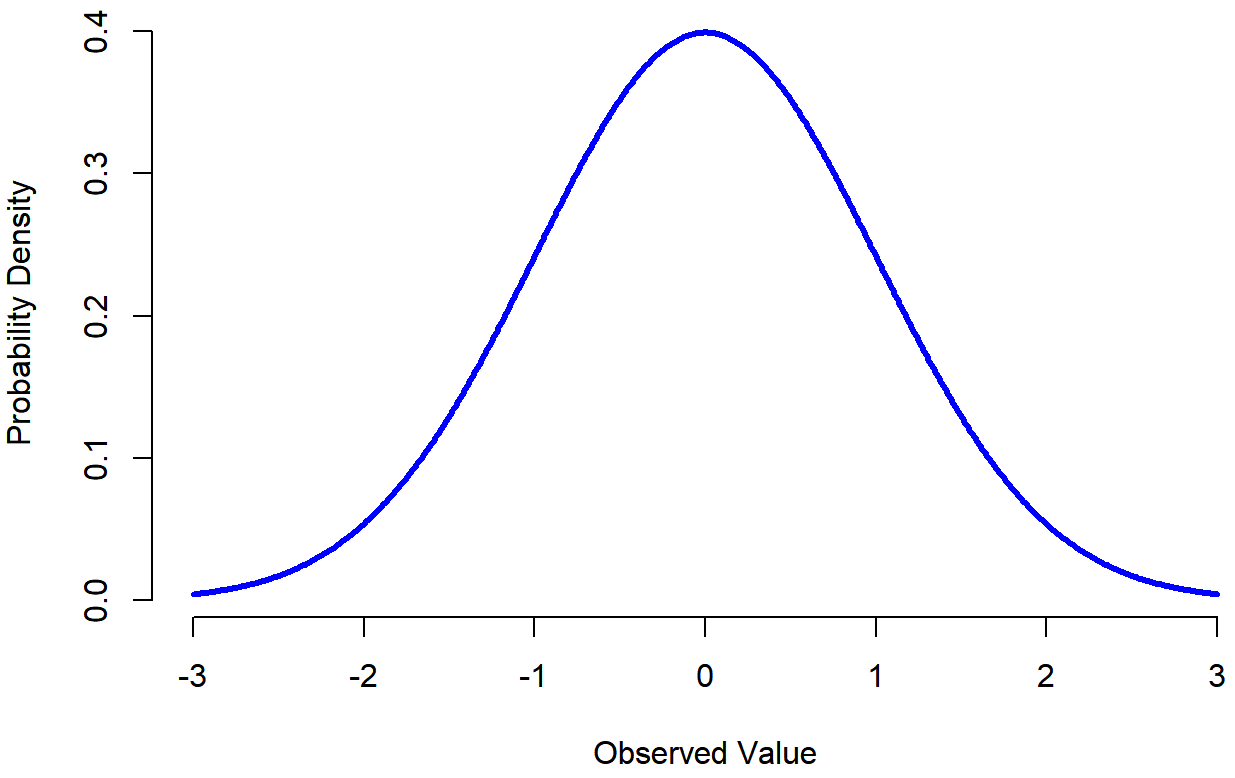
En lugar de enfocarnos en las matemáticas, intentemos tener una idea de lo que significa que una variable se distribuya normalmente. Para ello, eche un vistazo a la Figura 9.6, que traza una distribución normal con media μ=0 y desviación estándar σ=1. Se puede ver de dónde viene el nombre “curva de campana”: se parece un poco a una campana. Observe que, a diferencia de las gráficas que dibujé para ilustrar la distribución binomial, la imagen de la distribución normal en la Figura 9.6 muestra una curva suave en lugar de barras “similares a histograma”. Esta no es una elección arbitraria: la distribución normal es continua, mientras que el binomio es discreto. Por ejemplo, en el ejemplo de troquelado de la última sección, fue posible obtener 3 cráneos o 4 cráneos, pero imposible obtener 3.9 cráneos. Las cifras que dibujé en la sección anterior reflejaban este hecho: en la Figura 9.3, por ejemplo, hay una barra ubicada en X=3 y otra en X=4, pero no hay nada en el medio. Las cantidades continuas no tienen esta restricción. Por ejemplo, supongamos que estamos hablando del clima. La temperatura en un agradable día de primavera podría ser de 23 grados, 24 grados, 23.9 grados, o cualquier cosa intermedia ya que la temperatura es una variable continua, por lo que una distribución normal podría ser bastante apropiada para describir las temperaturas primaverales. 145
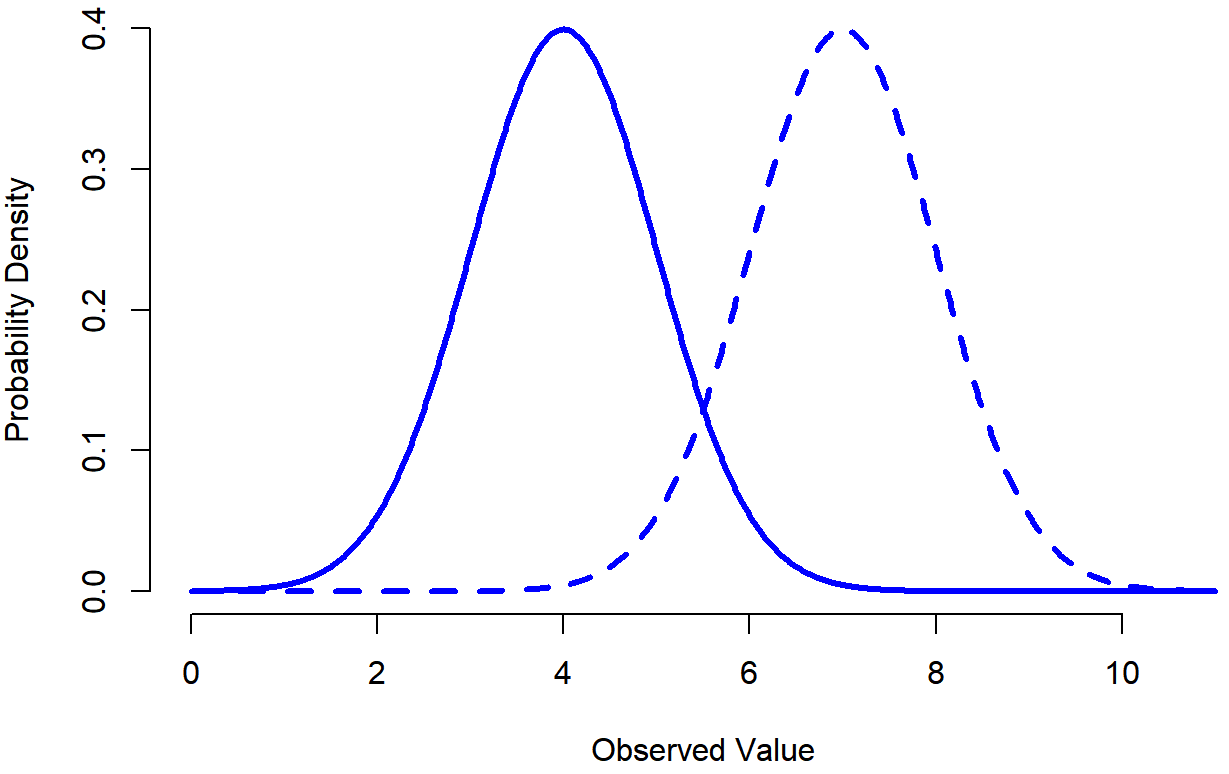
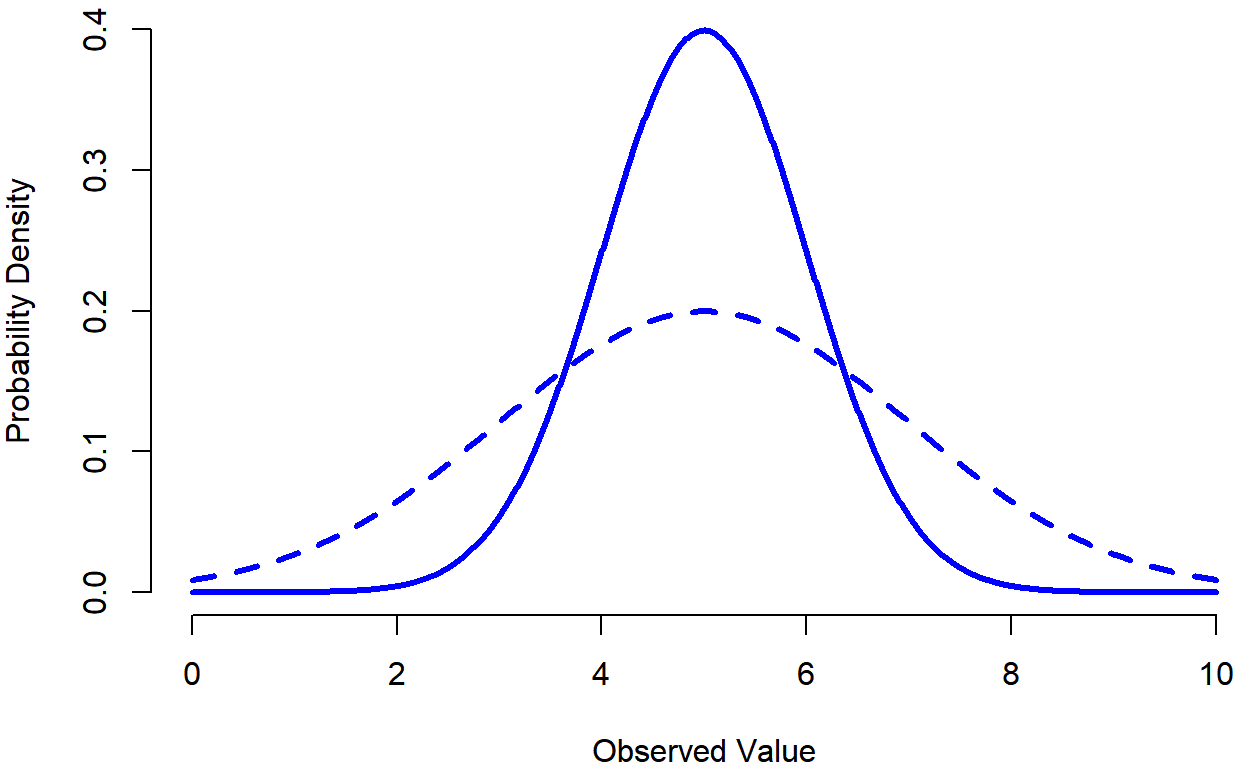
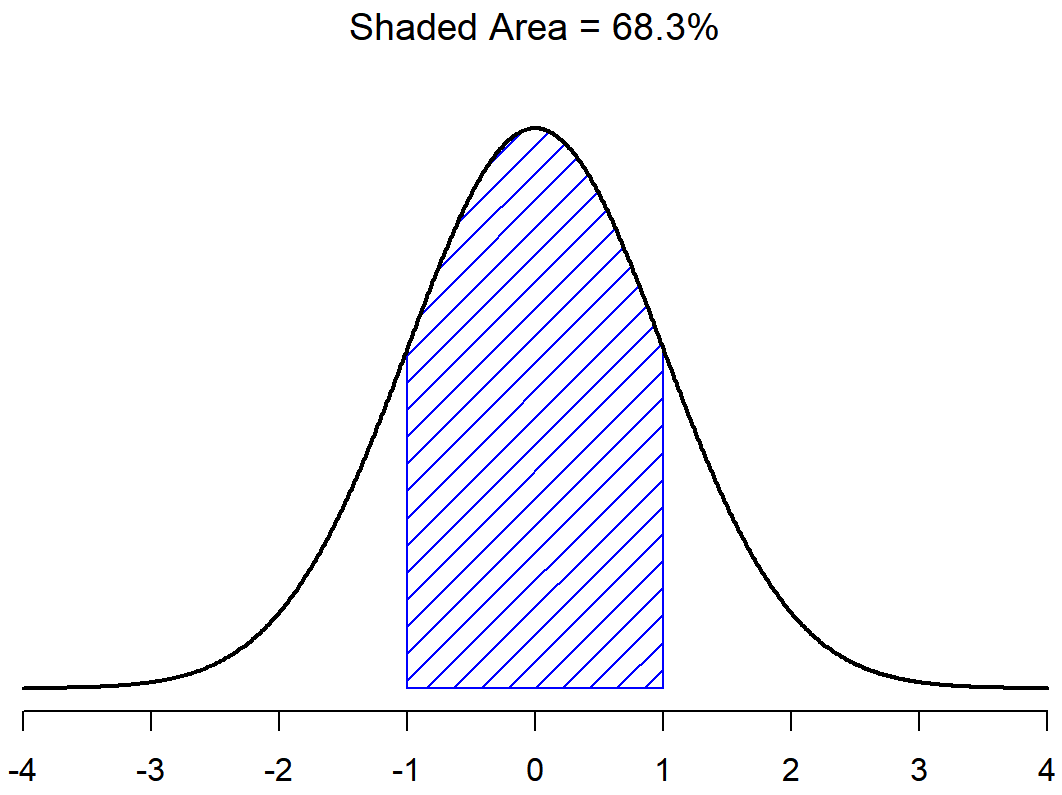
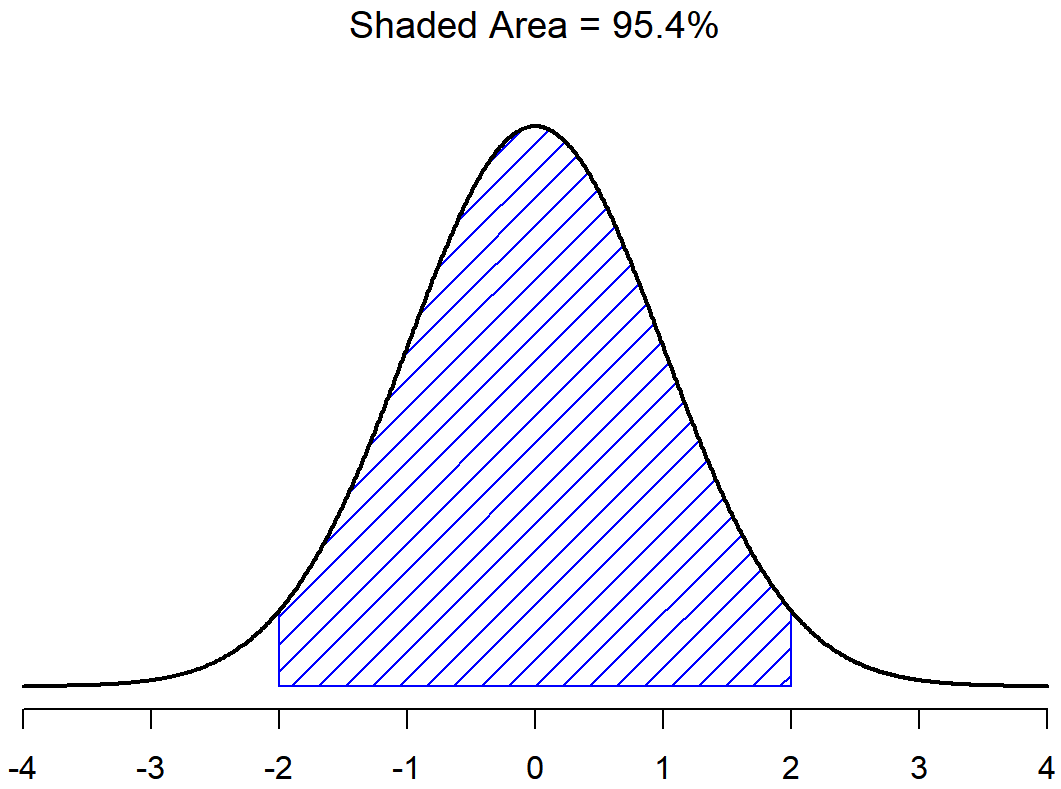
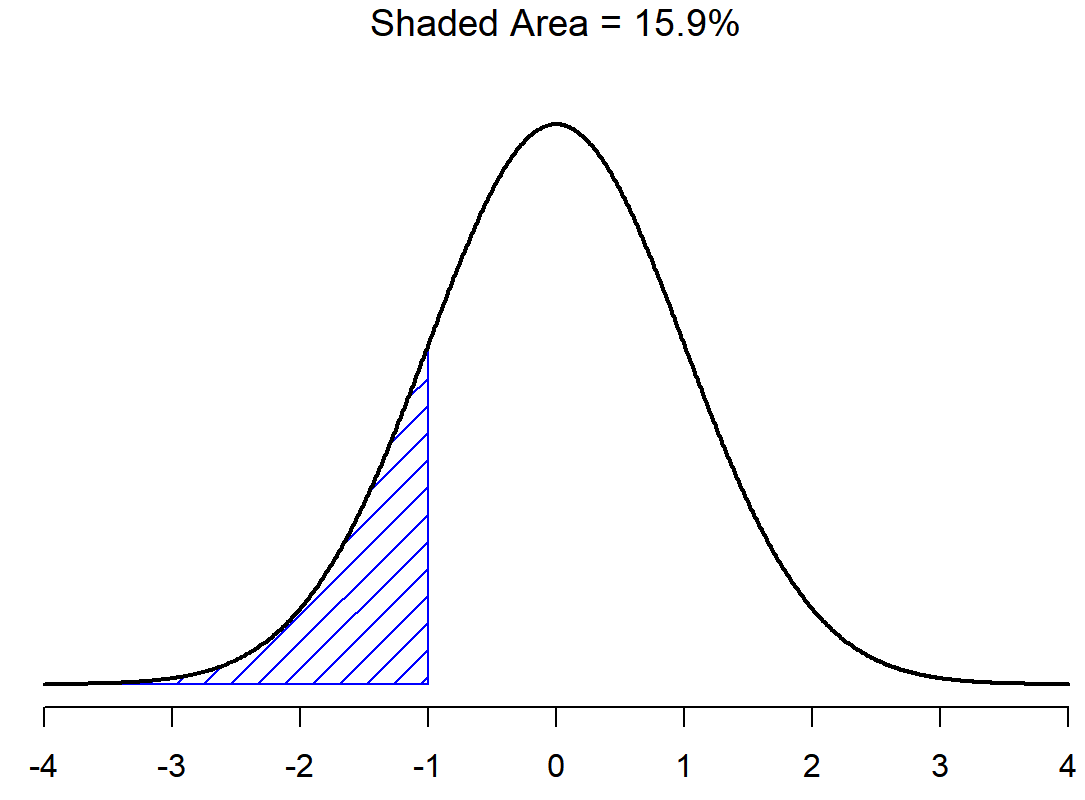
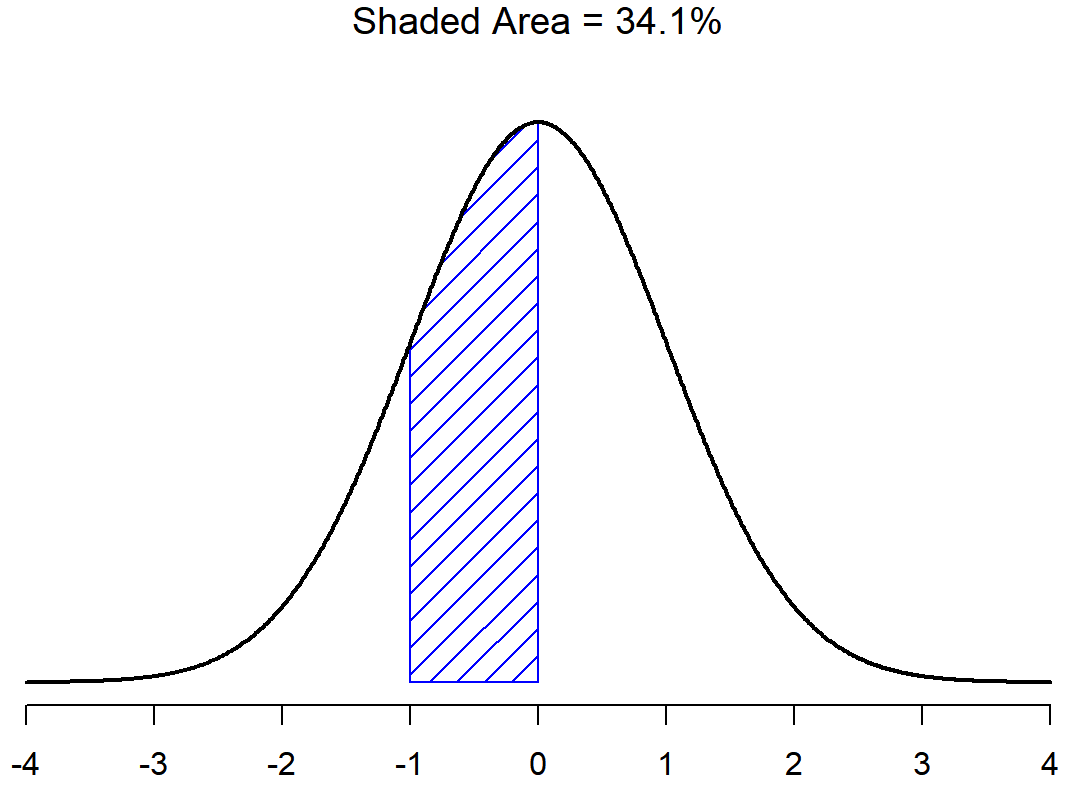
Con esto en mente, veamos si no podemos obtener una intuición de cómo funciona la distribución normal. En primer lugar, echemos un vistazo a lo que sucede cuando jugamos con los parámetros de la distribución. Para ello, la Figura 9.7 traza distribuciones normales que tienen medias diferentes, pero que tienen la misma desviación estándar. Como cabría esperar, todas estas distribuciones tienen el mismo “ancho”. La única diferencia entre ellos es que han sido desplazados hacia la izquierda o hacia la derecha. En todos los demás aspectos son idénticos. En contraste, si aumentamos la desviación estándar manteniendo constante la media, el pico de la distribución permanece en el mismo lugar, pero la distribución se hace más amplia, como se puede ver en la Figura 9.8. Observe, sin embargo, que cuando ampliamos la distribución, la altura del pico se contrae. Esto tiene que suceder: de la misma manera que las alturas de las barras que usamos para dibujar una distribución binomial discreta tienen que sumar a 1, el área total bajo la curva para la distribución normal debe ser igual a 1. Antes de seguir adelante, quiero señalar una característica importante de la distribución normal. Independientemente de cuál sea la media real y la desviación estándar, 68.3% del área se encuentra dentro de 1 desviación estándar de la media. De igual manera, 95.4% de la distribución se encuentra dentro de 2 desviaciones estándar de la media, y 99.7% de la distribución está dentro de 3 desviaciones estándar. Esta idea se ilustra en Figura?? .
Densidad de probabilidad
Hay algo que he estado tratando de ocultar a lo largo de mi discusión sobre la distribución normal, algo que algunos libros de texto introductorios omiten por completo. Puede que tengan razón al hacerlo: esta “cosa” que estoy ocultando es extraña y contradictoria incluso por los estándares ciertamente distorsionados que se aplican en la estadística. Afortunadamente, no es algo que necesites entender a un nivel profundo para poder hacer estadísticas básicas: más bien, es algo que empieza a ser importante más adelante cuando vas más allá de lo básico. Entonces, si no tiene sentido completo, no te preocupes: trata de asegurarte de seguir la esencia de la misma.
A lo largo de mi discusión sobre la distribución normal, ha habido una o dos cosas que no tienen mucho sentido. Quizás notó que el eje y en estas cifras está etiquetado como “Densidad de Probabilidad” en lugar de densidad. A lo mejor notaste que usé p (X) en lugar de P (X) al dar la fórmula para la distribución normal. Quizás te estés preguntando por qué R usa el prefijo “d” para funciones como dnorm (). Y tal vez, solo tal vez, has estado jugando con la función dnorm (), y accidentalmente escribes un comando como este:
dnorm( x = 1, mean = 1, sd = 0.1 )## [1] 3.989423Y si has hecho la última parte, probablemente estés muy confundido. Le he pedido a R que calcule la probabilidad de que x = 1, para una variable normalmente distribuida con media = 1 y desviación estándar sd = 0.1; y me dice que la probabilidad es de 3.99. Pero, como comentamos anteriormente, las probabilidades no pueden ser mayores que 1. Entonces, o he cometido un error, o eso no es una probabilidad.
Al final resulta que la segunda respuesta es correcta. Lo que hemos calculado aquí no es en realidad una probabilidad: es otra cosa. Para entender qué es ese algo, hay que dedicar un poco de tiempo a pensar en lo que realmente significa decir que X es una variable continua. Digamos que estamos hablando de la temperatura exterior. El termómetro me dice que son 23 grados, pero sé que eso no es realmente cierto. No son exactamente 23 grados. A lo mejor son 23.1 grados, pienso para mí mismo. Pero sé que eso tampoco es realmente cierto, porque en realidad podría ser de 23.09 grados. Pero, ya sé que... bueno, entiendes la idea. Lo complicado con cantidades genuinamente continuas es que nunca se sabe exactamente cuáles son.
Ahora piensa en lo que esto implica cuando hablamos de probabilidades. Supongamos que la temperatura máxima de mañana se muestrea a partir de una distribución normal con media 23 y desviación estándar 1. ¿Cuál es la probabilidad de que la temperatura sea exactamente de 23 grados? La respuesta es “cero”, o posiblemente, “un número tan cercano a cero que bien podría ser cero”. ¿Por qué es esto? Es como intentar lanzar un dardo a un tablero de dardos infinitamente pequeño: no importa cuán buena sea tu puntería, nunca lo golpearás. En la vida real nunca obtendrás un valor de exactamente 23. Siempre será algo así como 23.1 o 22.99998 o algo así. En otras palabras, no tiene sentido hablar de la probabilidad de que la temperatura sea exactamente de 23 grados. No obstante, en el lenguaje cotidiano, si te dijera que eran 23 grados afuera y resultó ser 22.9998 grados, probablemente no me llamarías mentiroso. Porque en el lenguaje cotidiano, “23 grados” suele significar algo así como “en algún lugar entre 22.5 y 23.5 grados”. Y si bien no se siente muy significativo preguntar sobre la probabilidad de que la temperatura sea exactamente de 23 grados, sí parece sensato preguntar sobre la probabilidad de que la temperatura se encuentre entre 22.5 y 23.5, o entre 20 y 30, o cualquier otro rango de temperaturas.
El objetivo de esta discusión es dejar claro que, cuando hablamos de distribuciones continuas, no es significativo hablar de la probabilidad de un valor específico. Sin embargo, de lo que podemos hablar es de la probabilidad de que el valor se encuentre dentro de un rango particular de valores. Para conocer la probabilidad asociada a un rango particular, lo que hay que hacer es calcular el “área bajo la curva”. Ya hemos visto este concepto: en las Figuras 9.9 y (fig:sdnorm1b), las áreas sombreadas mostradas representan probabilidades genuinas (por ejemplo, en la Figura 9.9 muestra la probabilidad de observar un valor que se encuentra dentro de 1 desviación estándar de la media).
Bien, eso explica parte de la historia. He explicado un poco sobre cómo se deben interpretar las distribuciones continuas de probabilidad (es decir, el área bajo la curva es lo clave), pero en realidad no he explicado qué calcula realmente la función dnorm (). Equivalentemente, ¿qué significa realmente la fórmula para p (x) que describí anteriormente? Obviamente, p (x) no describe una probabilidad, pero ¿qué es? El nombre para esta cantidad p (x) es una densidad de probabilidad, y en términos de las parcelas que hemos estado dibujando, corresponde a la altura de la curva. Las densidades en sí mismas no son significativas en sí mismas: pero están “amañadas” para asegurar que el área bajo la curva sea siempre interpretable como probabilidades genuinas. Para ser honestos, eso es todo lo que realmente necesitas saber por ahora. 146


