10.1: Muestras, Poblaciones y Muestreo
- Page ID
- 151460
En el preludio de la Parte I discutió el enigma de la inducción, y resaltó el hecho de que todo aprendizaje requiere que hagas suposiciones. Aceptando que esto es cierto, nuestra primera tarea es llegar a algunas suposiciones bastante generales sobre los datos que tengan sentido. Aquí es donde entra en juego la teoría del muestreo. Si la teoría de probabilidad es la base sobre la que se construye toda la teoría estadística, la teoría del muestreo es el marco alrededor del cual se puede construir el resto de la casa. La teoría del muestreo juega un papel muy importante en la especificación de los supuestos en los que se basan sus inferencias estadísticas. Y para hablar de “hacer inferencias” de la manera en que los estadísticos piensan al respecto, necesitamos ser un poco más explícitos sobre qué es de lo que estamos sacando inferencias (la muestra) y de qué es lo que estamos haciendo inferencias (la población).
En casi todas las situaciones de interés, lo que tenemos a nuestra disposición como investigadores es una muestra de datos. Podríamos haber realizado experimentos con algún número de participantes; una compañía de encuestas podría haber llamado por teléfono a algunas personas para hacer preguntas sobre intenciones de voto; etc. Independientemente: el conjunto de datos disponibles para nosotros es finito e incompleto. No podemos conseguir que todas las personas del mundo hagan nuestro experimento; una empresa de encuestas no tiene el tiempo ni el dinero para llamar a todos los votantes del país etc. En nuestra anterior discusión sobre estadísticas descriptivas (Capítulo 5, esta muestra era lo único que nos interesaba. Nuestro único objetivo era encontrar formas de describir, resumir y graficar esa muestra. Esto está a punto de cambiar.
Definición de una población
Una muestra es una cosa concreta. Puedes abrir un archivo de datos, y ahí están los datos de tu muestra. Una población, en cambio, es una idea más abstracta. Se refiere al conjunto de todas las personas posibles, o todas las observaciones posibles, sobre las que se quiere sacar conclusiones, y generalmente es mucho más grande que la muestra. En un mundo ideal, el investigador iniciaría el estudio con una idea clara de lo que es la población de interés, ya que el proceso de diseñar un estudio y probar hipótesis sobre los datos que produce sí depende de la población sobre la que se quiera hacer declaraciones. Sin embargo, eso no siempre sucede en la práctica: generalmente el investigador tiene una idea bastante vaga de lo que es la población y diseña el estudio lo mejor que puede sobre esa base.
A veces es fácil exponer la población de interés. Por ejemplo, en el ejemplo de “empresa de encuestas” que abrió el capítulo, la población estaba formada por todos los votantes inscritos en el momento del estudio —millones de personas—. La muestra fue un conjunto de 1000 personas que pertenecen todas a esa población. En la mayoría de las situaciones la situación es mucho menos sencilla. En un típico experimento psicológico, determinar la población de interés es un poco más complicado. Supongamos que realizo un experimento utilizando como participantes 100 estudiantes de pregrado. Mi objetivo, como científico cognitivo, es tratar de aprender algo sobre cómo funciona la mente. Entonces, cuál de los siguientes contaría como “la población”:
- ¿Todos los estudiantes de licenciatura en psicología de la Universidad de Adelaida?
- Estudiantes de licenciatura en psicología en general, ¿en cualquier parte del mundo?
- ¿Australianos que viven actualmente?
- Australianos de edades similares a mi muestra?
- ¿Alguien vivo actualmente?
- ¿Algún ser humano, pasado, presente o futuro?
- ¿Algún organismo biológico con un grado suficiente de inteligencia operando en un ambiente terrestre?
- ¿Algún ser inteligente?
Cada uno de estos define un verdadero grupo de entidades poseedoras de la mente, todas las cuales podrían ser de mi interés como científico cognitivo, y no está nada claro cuál debería ser la verdadera población de interés. Como otro ejemplo, consideremos el juego Wellesley-Croker que discutimos en el preludio. La muestra aquí es una secuencia específica de 12 victorias y 0 derrotas para Wellesley. ¿Cuál es la población?
- ¿Todos los resultados hasta que Wellesley y Croker llegaron a su destino?
- Todos los resultados si Wellesley y Croker hubieran jugado el juego por el resto de sus vidas?
- Todos los resultados si Wellseley y Croker vivieron para siempre y jugaron el juego hasta que el mundo se quedó sin colinas?
- Todos los resultados si creamos un conjunto infinito de universos paralelos y la pareja Wellesely/Croker hicieran conjeturas sobre las mismas 12 colinas en cada universo?
Nuevamente, no es obvio cuál es la población.
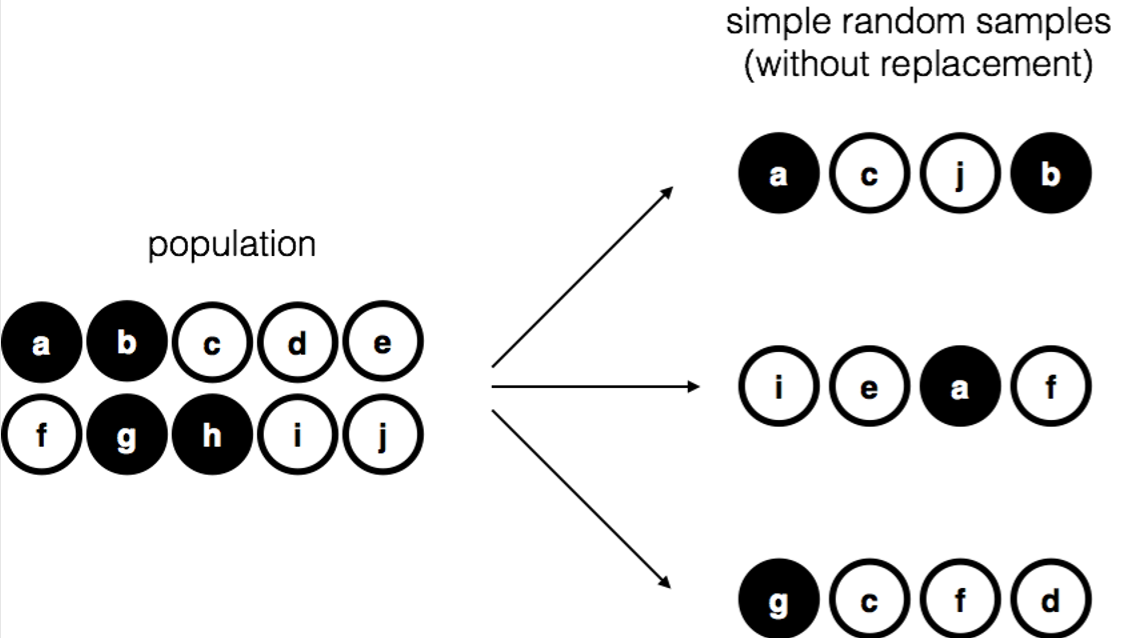
Independientemente de cómo defina a la población, el punto crítico es que la muestra es un subconjunto de la población, y nuestro objetivo es utilizar nuestro conocimiento de la muestra para hacer inferencias sobre las propiedades de la población. La relación entre ambos depende del procedimiento por el cual se seleccionó la muestra. Este procedimiento se conoce como método de muestreo, y es importante entender por qué es importante.
Para que las cosas sean simples, imaginemos que tenemos una bolsa que contiene 10 chips. Cada chip tiene una letra única impresa en él, por lo que podemos distinguir entre las 10 fichas. Las fichas vienen en dos colores, blanco y negro. Este conjunto de fichas es la población de interés, y se representa gráficamente a la izquierda de la Figura 10.1. Como puedes ver al mirar la foto, hay 4 chips negros y 6 chips blancos, pero claro que en la vida real no sabríamos eso a menos que busquemos en la bolsa. Ahora imagina que ejecutas el siguiente “experimento”: sacudes la bolsa, cierras los ojos y sacas 4 fichas sin volver a meter ninguna de ellas en la bolsa. Primero sale el chip a (negro), luego el chip c (blanco), luego j (blanco) y luego finalmente b (negro). Si quisieras, entonces podrías volver a poner todas las fichas en la bolsa y repetir el experimento, como se muestra en el lado derecho de la Figura 10.1. Cada vez se obtienen resultados diferentes, pero el procedimiento es idéntico en cada caso. El hecho de que un mismo procedimiento pueda conducir a diferentes resultados cada vez, nos referimos a él como un proceso aleatorio. 147 Sin embargo, debido a que sacudimos la bolsa antes de sacar las fichas, parece razonable pensar que cada ficha tiene las mismas posibilidades de ser seleccionada. Un procedimiento en el que cada miembro de la población tiene las mismas posibilidades de ser seleccionado se denomina muestra aleatoria simple. El hecho de que no volviéramos a meter las fichas en la bolsa después de sacarlas significa que no se puede observar lo mismo dos veces, y en tales casos se dice que las observaciones fueron muestreadas sin reemplazo.
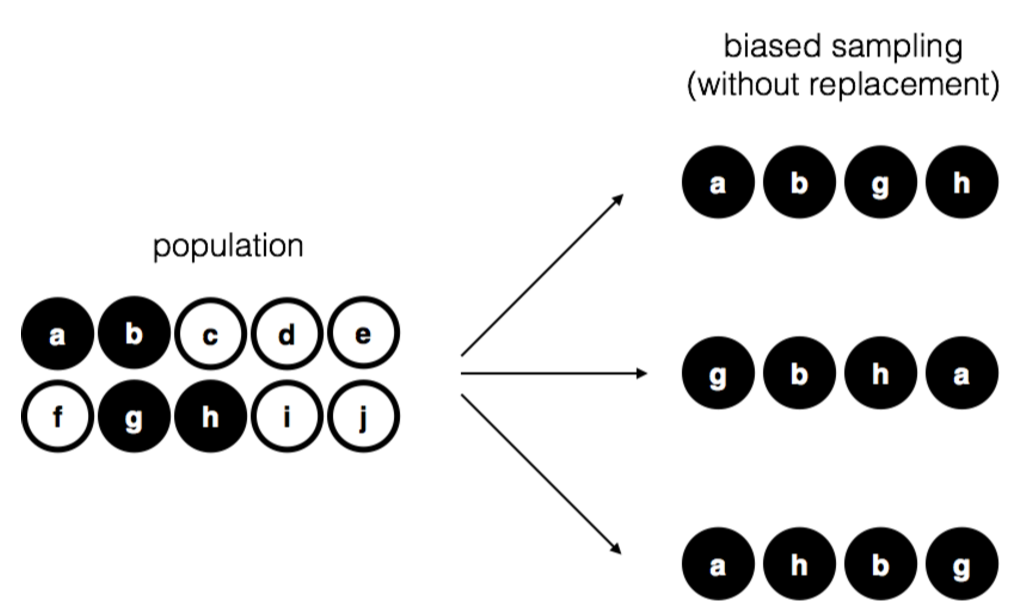
Para ayudar a comprender la importancia del procedimiento de muestreo, considere una forma alternativa en la que se podría haber realizado el experimento. Supongamos que mi hijo de 5 años había abierto la bolsa, y decidió sacar cuatro chips negros sin volver a meter ninguna de ellas en la bolsa. Este esquema de muestreo sesgado se representa en la Figura 10.2. Ahora considere el valor probatorio de ver 4 chips negros y 0 chips blancos. Claramente, depende del esquema de muestreo, ¿no? Si sabes que el esquema de muestreo está sesgado para seleccionar solo chips negros, entonces ¡una muestra que consiste solo en chips negros no te dice mucho sobre la población! Por esta razón, a los estadísticos les gusta mucho cuando un conjunto de datos puede considerarse una simple muestra aleatoria, porque facilita mucho el análisis de datos.
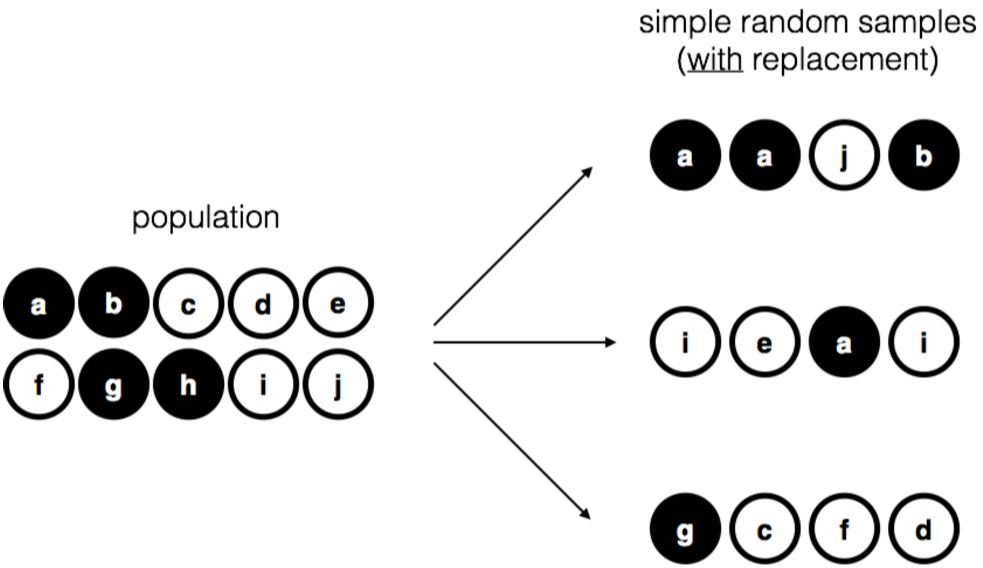
Vale la pena mencionar un tercer procedimiento. Esta vez cerramos los ojos, agitamos la bolsa y sacamos un chip. Esta vez, sin embargo, registramos la observación y luego volvemos a meter el chip en la bolsa. Nuevamente cerramos los ojos, agitamos la bolsa y sacamos un chip. Después repetimos este procedimiento hasta que tengamos 4 fichas. Los conjuntos de datos generados de esta manera siguen siendo simples muestras aleatorias, pero debido a que volvemos a poner las astillas en la bolsa inmediatamente después de dibujarlas se le conoce como una muestra con reemplazo. La diferencia entre esta situación y la primera es que es posible observar múltiples veces al mismo miembro de la población, como se ilustra en la Figura 10.3.
En mi experiencia, la mayoría de los experimentos de psicología tienden a ser muestreos sin reemplazo, porque a la misma persona no se le permite participar en el experimento dos veces. Sin embargo, la mayor parte de la teoría estadística se basa en el supuesto de que los datos surgen de una simple muestra aleatoria con reemplazo. En la vida real, esto muy raramente importa. Si la población de interés es grande (e.g., ¡tiene más de 10 entidades!) la diferencia entre el muestreo con y sin reemplazo es demasiado pequeña para preocuparse. La diferencia entre muestras aleatorias simples y muestras sesgadas, por otro lado, no es tan fácil de descartar.
La mayoría de las muestras no son simples muestras aleatorias
Como puede ver al mirar la lista de posibles poblaciones que mostré anteriormente, es casi imposible obtener una muestra aleatoria simple de la mayoría de las poblaciones de interés. Cuando realizo experimentos, consideraría un milagro menor si mis participantes resultaran ser una muestra aleatoria de los estudiantes de licenciatura en psicología de la universidad de Adelaida, aunque esta es, con mucho, la población más estrecha a la que podría querer generalizar. Una discusión exhaustiva de otros tipos de esquemas de muestreo está más allá del alcance de este libro, pero para darle una idea de lo que hay ahí afuera enumeraré algunos de los más importantes:
- Muestreo estratificado. Supongamos que su población está (o puede ser) dividida en varias subpoblaciones diferentes, o estratos. Quizás estés realizando un estudio en varios sitios diferentes, por ejemplo. En lugar de tratar de muestrear aleatoriamente de la población en su conjunto, en su lugar, intenta recolectar una muestra aleatoria separada de cada uno de los estratos. El muestreo estratificado a veces es más fácil de hacer que el muestreo aleatorio simple, especialmente cuando la población ya está dividida en los distintos estratos. También puede ser más eficiente que el muestreo aleatorio simple, especialmente cuando algunas de las subpoblaciones son raras. Por ejemplo, al estudiar esquizofrenia sería mucho mejor dividir la población en dos 148 estratos (esquizofrénicos y no esquizofrénicos), para luego muestrear un número igual de personas de cada grupo. Si seleccionaste personas al azar, obtendrías tan pocas personas esquizofrénicas en la muestra que tu estudio sería inútil. Este tipo específico de muestreo estratificado se conoce como sobremuestreo porque hace un intento deliberado de sobrerepresentar grupos raros.
- El muestreo de bolas de nieve es una técnica que resulta especialmente útil cuando se toma de muestras de una población “oculta” o de difícil acceso, y es especialmente común en las ciencias sociales. Por ejemplo, supongamos que los investigadores quieren realizar una encuesta de opinión entre personas transgénero. Es posible que el equipo de investigación solo tenga datos de contacto de algunas personas trans, por lo que la encuesta comienza pidiéndoles que participen (etapa 1). Al final de la encuesta, se pide a los participantes que proporcionen datos de contacto de otras personas que puedan querer participar. En la etapa 2, se encuestan esos nuevos contactos. El proceso continúa hasta que los investigadores cuenten con datos suficientes. La gran ventaja del muestreo de bolas de nieve es que te obtiene datos en situaciones que de otro modo serían imposibles de obtener. En el lado estadístico, la principal desventaja es que la muestra es altamente no aleatoria, y no aleatoria en formas difíciles de abordar. En el lado de la vida real, la desventaja es que el procedimiento puede ser poco ético si no se maneja bien, porque las poblaciones ocultas suelen estar ocultas por alguna razón. Elegí a las personas transgénero como ejemplo aquí para destacar esto: si no tuviste cuidado podrías terminar sacando a personas que no quieren ser descubiertas (muy, muy mala forma), e incluso si no cometes ese error puede ser intrusivo usar las redes sociales de las personas para estudiarlas. Ciertamente es muy difícil obtener el consentimiento informado de las personas antes de contactarlas, sin embargo, en muchos casos el simple hecho de contactarlos y decir “hey queremos estudiarte” puede ser hiriente. Las redes sociales son cosas complejas, y el hecho de que puedas usarlas para obtener datos no siempre significa que debas hacerlo.
- El muestreo de conveniencia es más o menos lo que parece. Las muestras se eligen de una manera que sea conveniente para el investigador, y no se seleccionan al azar de la población de interés. El muestreo de bola de nieve es un tipo de muestreo de conveniencia, pero hay muchos otros. Un ejemplo común en psicología son los estudios que se basan en estudiantes de licenciatura en psicología. Estas muestras son generalmente no aleatorias en dos aspectos: en primer lugar, la dependencia de estudiantes de psicología de pregrado significa automáticamente que sus datos están restringidos a una sola subpoblación. En segundo lugar, los estudiantes suelen elegir en qué estudios participan, por lo que la muestra es un subconjunto autoseleccionado de estudiantes de psicología, no un subconjunto seleccionado al azar. En la vida real, la mayoría de los estudios son muestras de conveniencia de una forma u otra. Esto a veces es una limitación severa, pero no siempre.
mucho importa si no tienes una simple muestra aleatoria?
Bien, entonces la recolección de datos del mundo real tiende a no involucrar agradables muestras aleatorias simples. ¿Eso importa? Un poco de pensamiento debería dejarte claro que puede importar si tus datos no son una simple muestra aleatoria: solo piensa en la diferencia entre las Figuras 10.1 y 10.2. Sin embargo, no es tan malo como suena. Algunos tipos de muestras sesgadas no son problemáticos. Por ejemplo, cuando se usa una técnica de muestreo estratificado, realmente sabes cuál es el sesgo porque lo creaste deliberadamente, a menudo para aumentar la efectividad de tu estudio, y hay técnicas estadísticas que puedes usar para ajustar los sesgos que has introducido (¡no cubierto en este libro!). Entonces en esas situaciones no es un problema.
Sin embargo, de manera más general, es importante recordar que el muestreo aleatorio es un medio para un fin, no el final en sí mismo. Supongamos que ha confiado en una muestra de conveniencia y, como tal, puede asumir que es sesgada. Un sesgo en tu método de muestreo solo es un problema si te hace sacar conclusiones equivocadas. Cuando se ve desde esa perspectiva, yo diría que no necesitamos que la muestra se genere aleatoriamente en todos los aspectos: solo necesitamos que sea aleatoria con respecto al fenómeno de interés psicológicamente relevante. Supongamos que estoy haciendo un estudio mirando a la capacidad de la memoria de trabajo. En el estudio 1, en realidad tengo la capacidad de tomar muestras al azar de todos los seres humanos actualmente vivos, con una excepción: solo puedo muestrear personas nacidas un lunes. En el estudio 2, puedo muestrear aleatoriamente de la población australiana. Quiero generalizar mis resultados a la población de todos los humanos vivos. ¿Qué estudio es mejor? La respuesta, obviamente, es el estudio 1. ¿Por qué? Porque no tenemos razón para pensar que ser “nacido un lunes” tiene alguna relación interesante con la capacidad de memoria de trabajo. En contraste, puedo pensar en varias razones por las que “ser australiano” podría importar. Australia es un país rico e industrializado con un sistema educativo muy bien desarrollado. Las personas que crecen en ese sistema habrán tenido experiencias de vida mucho más similares a las experiencias de las personas que diseñaron las pruebas de capacidad de memoria de trabajo. Esta experiencia compartida podría traducirse fácilmente en creencias similares sobre cómo “tomar una prueba”, una suposición compartida sobre cómo funciona la experimentación psicológica, etc. Estas cosas en realidad podrían importar. Por ejemplo, el estilo de “toma de pruebas” podría haber enseñado a los participantes australianos cómo dirigir su atención exclusivamente en materiales de prueba bastante abstractos en relación con personas que no han crecido en un entorno similar; lo que lleva a una imagen engañosa de lo que es la capacidad de la memoria de trabajo.
Hay dos puntos ocultos en esta discusión. En primer lugar, a la hora de diseñar tus propios estudios, es importante pensar en qué población te importa, y esforzarte por muestrear de una manera que sea apropiada para esa población. En la práctica, generalmente te ves obligado a aguantar una “muestra de conveniencia” (por ejemplo, profesores de psicología prueban estudiantes de psicología porque esa es la forma menos costosa de recopilar datos, y nuestras arcas no están desbordadas exactamente de oro), pero si es así, al menos deberías pasar algún tiempo pensando en lo que peligros de esta práctica podrían ser.
En segundo lugar, si vas a criticar el estudio de otra persona porque ha utilizado una muestra de conveniencia en lugar de muestrear laboriosamente aleatoriamente de toda la población humana, al menos ten la cortesía de ofrecer una teoría específica sobre cómo esto podría haber distorsionado los resultados. Recuerden, todos en la ciencia son conscientes de este tema, y hacen lo que pueden para aliviarlo. El mero hecho de señalar que “el estudio solo incluyó a personas del grupo BLAH” es totalmente inútil, y raya en ser insultantes para los investigadores, quienes por supuesto están al tanto del tema. Simplemente no pasan a estar en posesión del suministro infinito de tiempo y dinero requerido para construir la muestra perfecta. En definitiva, si se quiere ofrecer una crítica responsable del proceso de muestreo, entonces sea útil. No es útil repetir los truismos ciegamente obvios sobre los que he estado divagando en esta sección.
Parámetros poblacionales y estadísticas muestrales
Bien. Dejando de lado los espinosos problemas metodológicos asociados con la obtención de una muestra aleatoria y mi tendencia bastante desafortunada a despotricar sobre la crítica metodológica perezosa, consideremos un tema ligeramente diferente. Hasta este punto hemos estado hablando de poblaciones como podría ser un científico. Para un psicólogo, una población podría ser un grupo de personas. Para un ecologista, una población podría ser un grupo de osos. En la mayoría de los casos las poblaciones que les importan a los científicos son cosas concretas que realmente existen en el mundo real. Los estadísticos, sin embargo, son muy graciosos. Por un lado, les interesan los datos del mundo real y la ciencia real de la misma manera que lo están los científicos. Por otro lado, también operan en el ámbito de la abstracción pura en la forma en que lo hacen los matemáticos. Como consecuencia, la teoría estadística tiende a ser un poco abstracta en cómo se define una población. De la misma manera que los investigadores psicológicos operacionalizan nuestras ideas teóricas abstractas en términos de mediciones concretas (Sección 2.1, los estadísticos operacionalizan el concepto de “población” en términos de objetos matemáticos con los que saben trabajar. Ya te has encontrado con estos objetos en el Capítulo 9: se llaman distribuciones de probabilidad.
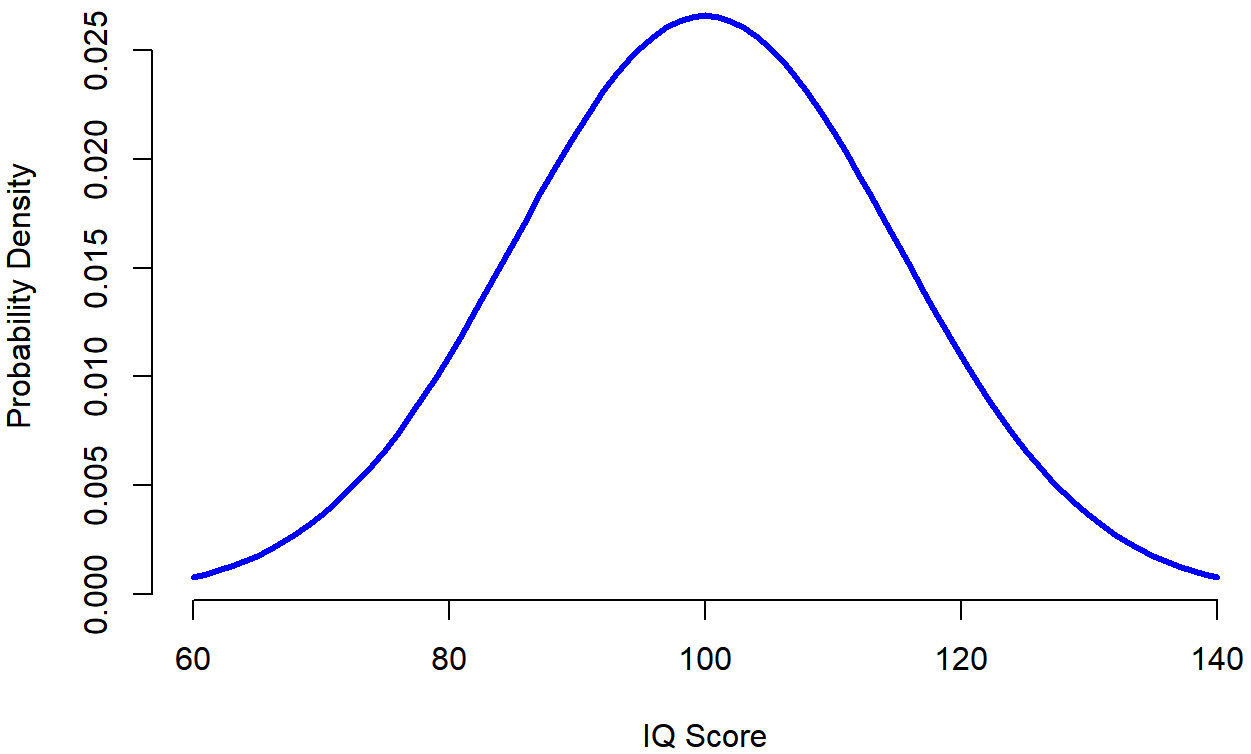
La idea es bastante sencilla. Digamos que estamos hablando de puntajes de CI. Para un psicólogo, la población de interés es un grupo de humanos reales que tienen puntajes de coeficiente intelectual. Un estadístico “simplifica” esto definiendo operacionalmente a la población como la distribución de probabilidad representada en la Figura?? . Las pruebas de CI están diseñadas para que el coeficiente intelectual promedio sea de 100, la desviación estándar de las puntuaciones de CI sea de 15 y la distribución de las puntuaciones de CI sea normal. Estos valores son referidos como los parámetros poblacionales porque son características de toda la población. Es decir, decimos que la media poblacional μ es 100, y la desviación estándar poblacional σ es 15.
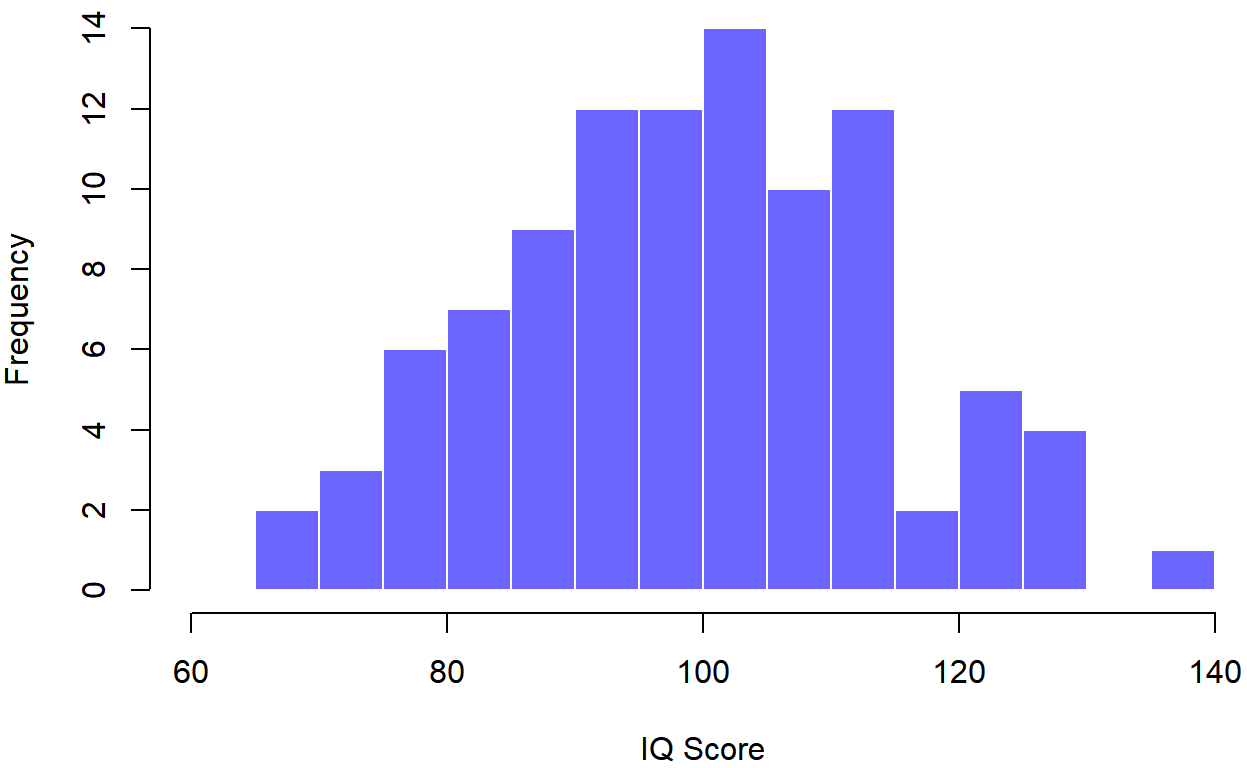
## [1] "n= 100 mean= 99.6064025956605 sd= 16.0047604703873"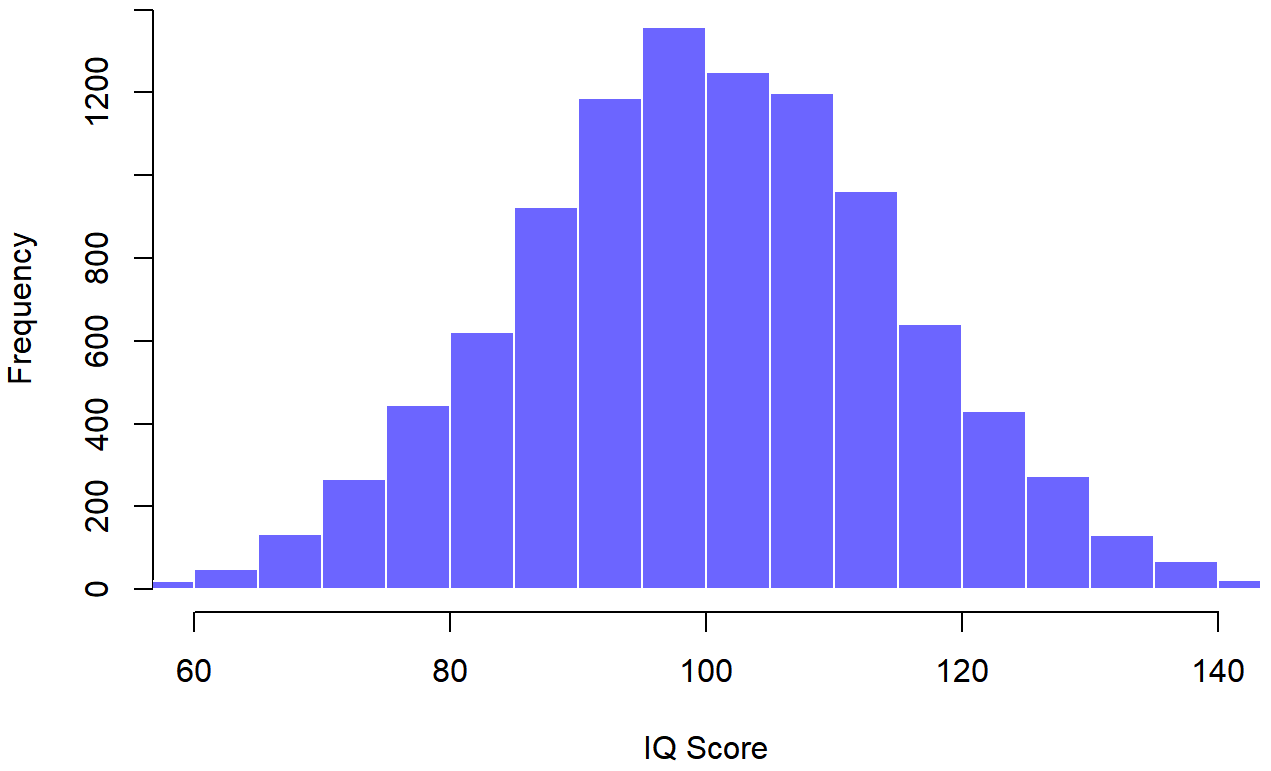
## [1] "n= 10000 mean= 100.096924966188 sd= 14.9554812898374"Ahora supongamos que hago un experimento. Selecciono 100 personas al azar y administro una prueba de CI, dándome una simple muestra aleatoria de la población. Mi muestra consistiría en una colección de números como este:
106 101 98 80 74 ... 107 72 100Cada una de estas puntuaciones de CI se muestrea a partir de una distribución normal con media 100 y desviación estándar 15. Entonces, si grafico un histograma de la muestra, obtengo algo como el que se muestra en la Figura 10.4b. Como puede ver, el histograma es aproximadamente la forma correcta, pero es una aproximación muy cruda a la verdadera distribución poblacional que se muestra en la Figura 10.4a. Cuando calculo la media de mi muestra, obtengo un número que es bastante cercano a la media poblacional 100 pero no idéntico. En este caso, resulta que las personas de mi muestra tienen un coeficiente intelectual medio de 98.5, y la desviación estándar de sus puntajes de CI es de 15.9. Estas estadísticas muestrales son propiedades de mi conjunto de datos, y aunque son bastante similares a los verdaderos valores poblacionales, no son los mismos. En general, las estadísticas de muestra son las cosas que puedes calcular a partir de tu conjunto de datos, y los parámetros de población son las cosas que quieres aprender. Más adelante en este capítulo hablaré sobre cómo puedes estimar los parámetros de población usando tus estadísticas de muestra (Sección 10.4 y cómo calcular la confianza que tienes en tus estimaciones (Sección 10.5 pero antes de llegar a eso hay algunas ideas más en la teoría del muestreo que necesitas conocer.


