10.3: Distribuciones de muestreo y teorema del límite central
- Page ID
- 151476
La ley de los grandes números es una herramienta muy poderosa, pero no va a ser lo suficientemente buena para responder a todas nuestras preguntas. Entre otras cosas, todo lo que nos da es una “garantía a largo plazo”. A la larga, si de alguna manera fuéramos capaces de recopilar una cantidad infinita de datos, entonces la ley de grandes números garantiza que nuestras estadísticas muestrales serán correctas. Pero como John Maynard Keynes argumentó en economía, una garantía a largo plazo es de poca utilidad en la vida real:
[El] a largo plazo es una guía engañosa para la actualidad. A la larga estamos todos muertos. Los economistas se pusieron una tarea demasiado fácil, demasiado inútil, si en temporadas tempestuosas sólo nos pueden decir, que cuando la tormenta ha pasado mucho tiempo, el océano vuelve a estar plano. Keynes (1923)
Como en economía, también en psicología y estadística. No basta con saber que eventualmente llegaremos a la respuesta correcta al calcular la media muestral. Saber que un conjunto de datos infinitamente grande me dirá que el valor exacto de la media de la población es frío confort cuando mi conjunto de datos real tiene un tamaño de muestra de N=100. En la vida real, entonces, debemos saber algo sobre el comportamiento de la media muestral cuando se calcula a partir de un conjunto de datos más modesto!
Distribución muestral de la media
Con esto en mente, abandonemos la idea de que nuestros estudios tendrán tamaños de muestra de 10000, y consideremos efectivamente un experimento muy modesto. En esta ocasión tomaremos muestras de N=5 personas y mediremos sus puntajes de CI. Como antes, puedo simular este experimento en R usando la función rnorm ():
> IQ.1 <- round( rnorm(n=5, mean=100, sd=15 ))
> IQ.1
[1] 90 82 94 99 110El coeficiente intelectual medio en esta muestra resulta ser exactamente 95. No es sorprendente que esto sea mucho menos preciso que el experimento anterior. Ahora imagina que decidí replicar el experimento. Es decir, repito el procedimiento lo más cerca posible: Muestreo aleatoriamente a 5 nuevas personas y mido su coeficiente intelectual. Nuevamente, R me permite simular los resultados de este procedimiento:
> IQ.2 <- round( rnorm(n=5, mean=100, sd=15 ))
> IQ.2
[1] 78 88 111 111 117En esta ocasión, el coeficiente intelectual medio en mi muestra es 101. Si repito el experimento 10 veces obtengo los resultados mostrados en la Tabla ?? , y como puede ver la media de la muestra varía de una réplica a la siguiente.
| NANA | Persona.1 | Persona.2 | Persona.3 | Persona.4 | Persona.5 | Muestra.Media | subtituir |
|---|---|---|---|---|---|---|---|
| Replicación 1 | 90 | 82 | 94 | 99 | 110 | 95.0 | Diez repeticiones del experimento IQ, cada una con un tamaño de muestra de N=5. |
| Replicación 2 | 78 | 88 | 111 | 111 | 117 | 101.0 | Diez repeticiones del experimento IQ, cada una con un tamaño de muestra de N=5. |
| Replicación 3 | 111 | 122 | 91 | 98 | 86 | 101.6 | Diez repeticiones del experimento IQ, cada una con un tamaño de muestra de N=5. |
| Replicación 4 | 98 | 96 | 119 | 99 | 107 | 103.8 | Diez repeticiones del experimento IQ, cada una con un tamaño de muestra de N=5. |
| Replicación 5 | 105 | 113 | 103 | 103 | 98 | 104.4 | Diez repeticiones del experimento IQ, cada una con un tamaño de muestra de N=5. |
| Replicación 6 | 81 | 89 | 93 | 85 | 114 | 92.4 | Diez repeticiones del experimento IQ, cada una con un tamaño de muestra de N=5. |
| Replicación 7 | 100 | 93 | 108 | 98 | 133 | 106.4 | Diez repeticiones del experimento IQ, cada una con un tamaño de muestra de N=5. |
| Replicación 8 | 107 | 100 | 105 | 117 | 85 | 102.8 | Diez repeticiones del experimento IQ, cada una con un tamaño de muestra de N=5. |
| Replicación 9 | 86 | 119 | 108 | 73 | 116 | 100.4 | Diez repeticiones del experimento IQ, cada una con un tamaño de muestra de N=5. |
| Replicación 10 | 95 | 126 | 112 | 120 | 76 | 105.8 | Diez repeticiones del experimento IQ, cada una con un tamaño de muestra de N= |
Ahora suponga que decidí seguir adelante de esta manera, replicando este experimento de “cinco puntajes de coeficiente intelectual” una y otra vez. Cada vez que replico el experimento anoto la media de la muestra. Con el tiempo, estaría acumulando un nuevo conjunto de datos, en el que cada experimento genera un solo punto de datos. Las primeras 10 observaciones de mi conjunto de datos son las medias muestrales listadas en la Tabla?? , así que mi conjunto de datos comienza así:
95.0 101.0 101.6 103.8 104.4 ...¿Y si continué así por 10,000 repeticiones y luego dibujé un histograma? Usando los poderes mágicos de R eso es exactamente lo que hice, y puedes ver los resultados en la Figura 10.5. Como ilustra esta imagen, el promedio de 5 puntajes de CI suele estar entre 90 y 110. Pero lo que es más importante, lo que destaca es que si replicamos un experimento una y otra vez, ¡lo que terminamos es una distribución de medios de muestra! Esta distribución tiene un nombre especial en la estadística: se llama distribución muestral de la media.
Las distribuciones de muestreo son otra idea teórica importante en estadística, y son cruciales para comprender el comportamiento de las muestras pequeñas. Por ejemplo, cuando ejecuté el primer experimento de “cinco puntajes de coeficiente intelectual”, la media muestral resultó ser 95. Sin embargo, lo que nos dice la distribución muestral en la Figura 10.5 es que el experimento de “cinco puntajes de coeficiente intelectual” no es muy preciso. Si repito el experimento, la distribución muestral me dice que puedo esperar ver una media muestral en cualquier lugar entre 80 y 120.
¡Existen distribuciones de muestreo para cualquier estadística de muestra!
Una cosa a tener en cuenta a la hora de pensar en distribuciones de muestreo es que cualquier estadística de muestra que le interese calcular tiene una distribución de muestreo. Por ejemplo, supongamos que cada vez que repliqué el experimento de “cinco puntajes de coeficiente intelectual” escribí el puntaje de CI más grande del experimento. Esto me daría un conjunto de datos que comenzó así:
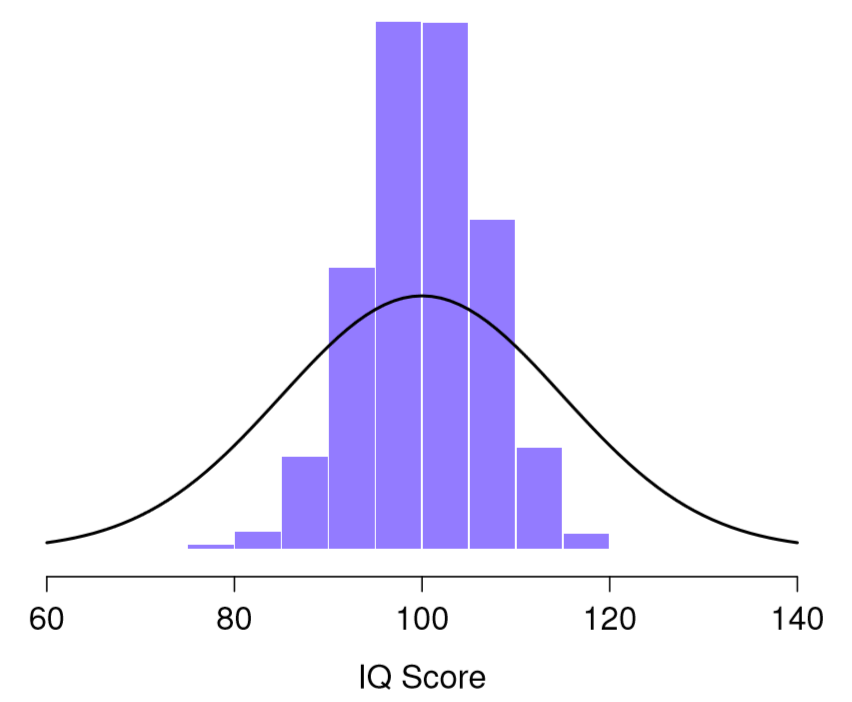
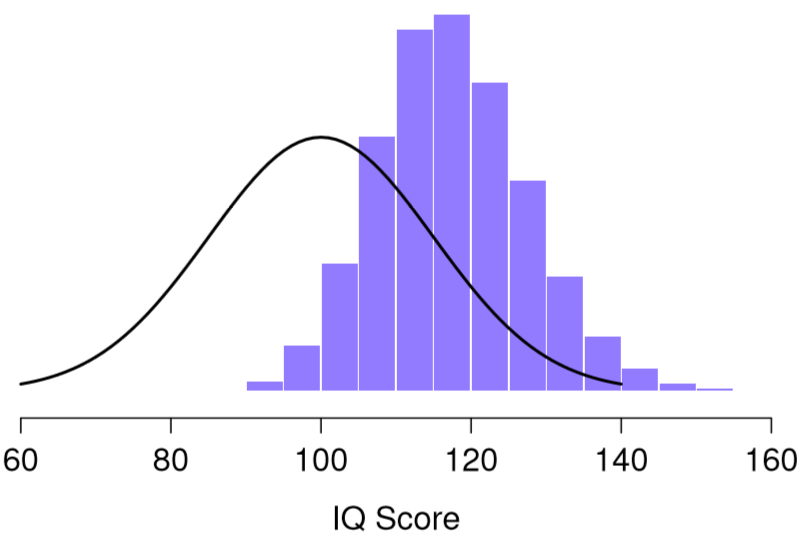
110 117 122 119 113 ... Hacer esto una y otra vez me daría una distribución muestreada muy diferente, es decir, la distribución muestral del máximo. La distribución muestral del máximo de 5 puntajes de CI se muestra en la Figura 10.6. No es sorprendente que si eliges 5 personas al azar y luego encuentras a la persona con el puntaje de CI más alto, van a tener un coeficiente intelectual superior al promedio. La mayoría de las veces terminarás con alguien cuyo coeficiente intelectual se mide en el rango de 100 a 140.
teorema del límite central
Una ilustración de cómo la distribución muestral de la media depende del tamaño de la muestra. En cada panel, generé 10,000 muestras de datos de CI, y calculé el coeficiente intelectual medio observado dentro de cada uno de estos conjuntos de datos. Los histogramas en estas parcelas muestran la distribución de estas medias (es decir, la distribución muestral de la media). Cada puntaje de CI individual se extrajo de una distribución normal con media 100 y desviación estándar 15, que se muestra como la línea negra continua).
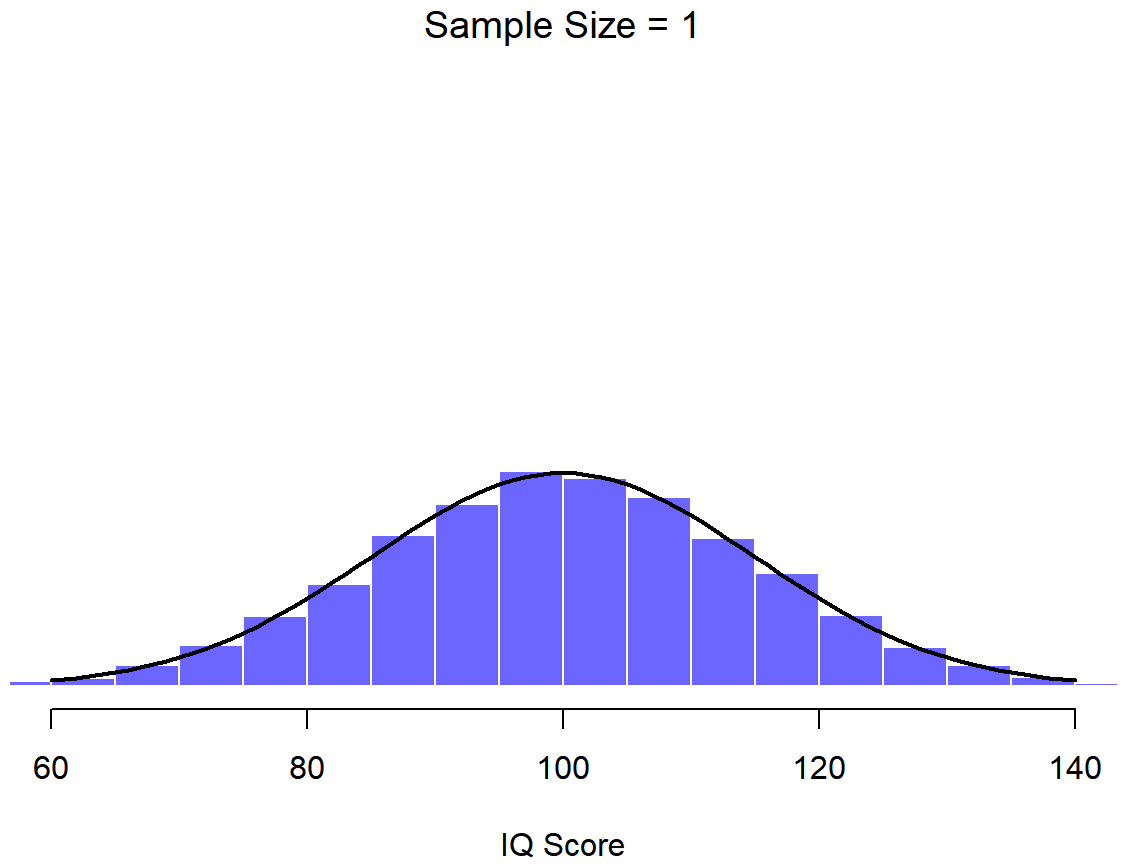
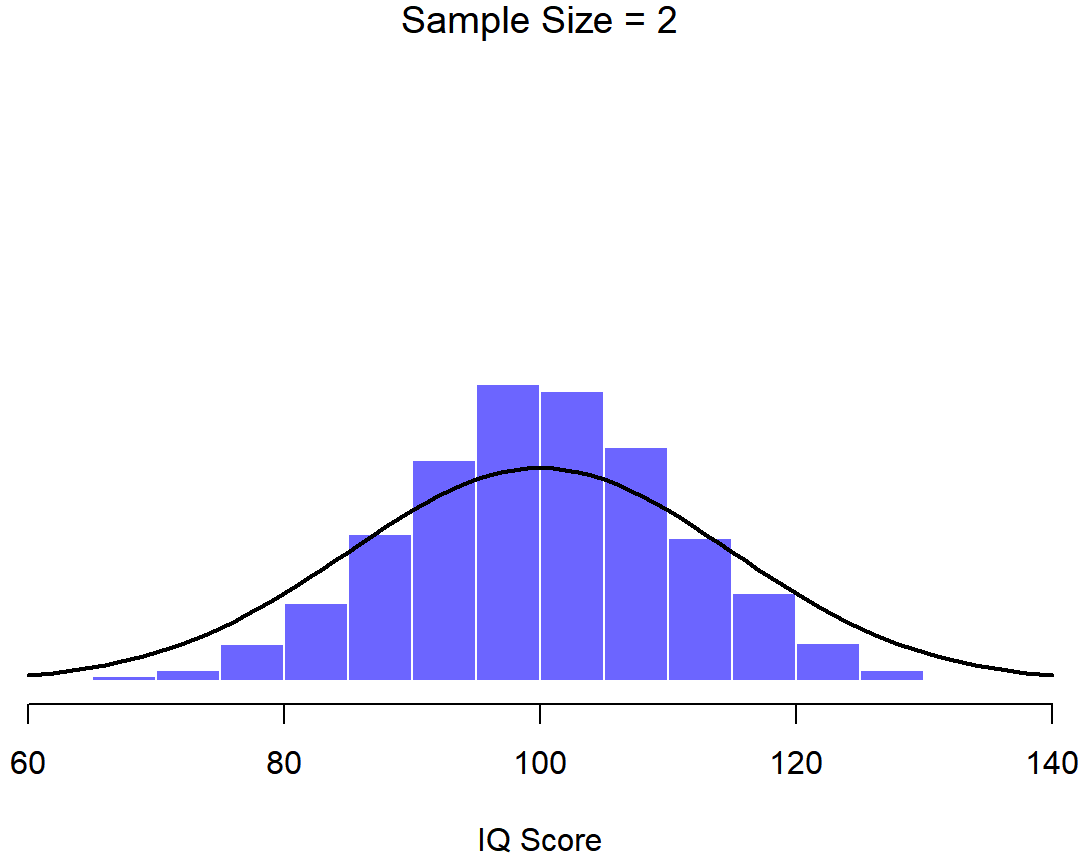
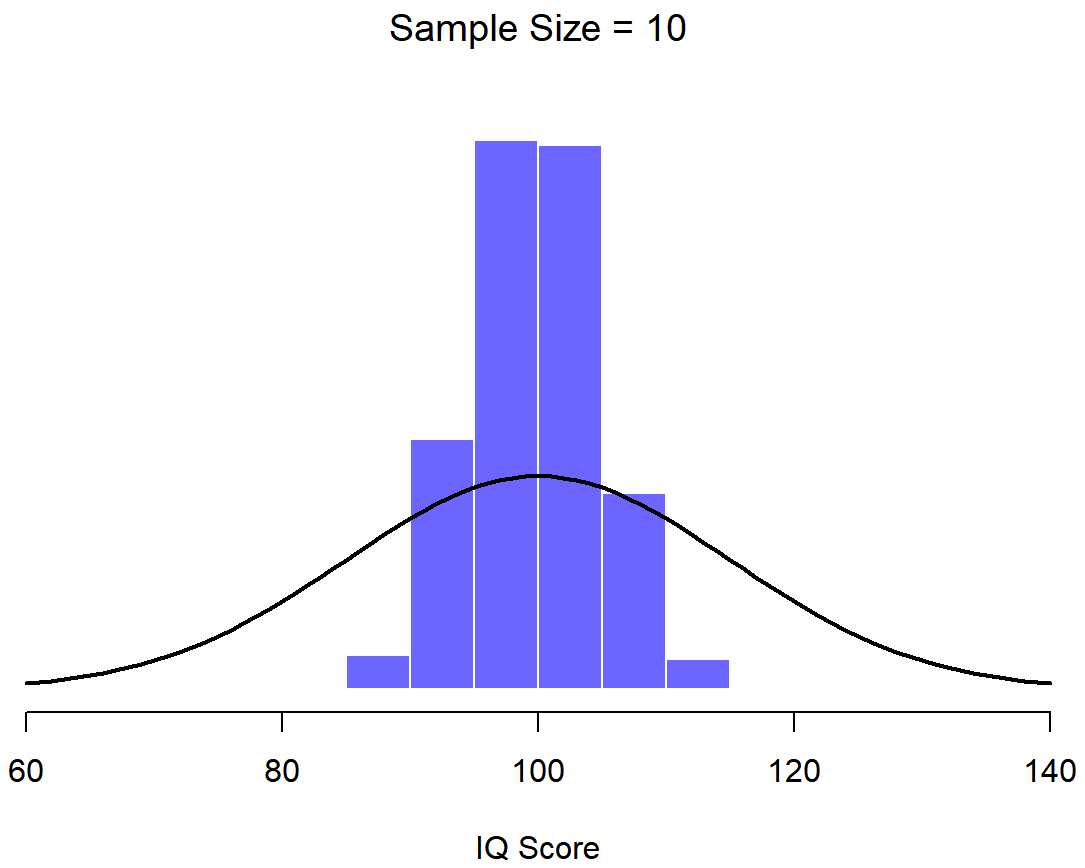
En este punto espero que tenga un sentido bastante bueno de qué son las distribuciones de muestreo, y en particular cuál es la distribución muestral de la media. En esta sección quiero hablar de cómo cambia la distribución muestral de la media en función del tamaño de la muestra. Intuitivamente, ya conoces parte de la respuesta: si solo tienes unas pocas observaciones, es probable que la media de la muestra sea bastante inexacta: si replicas un pequeño experimento y recalculas la media obtendrás una respuesta muy diferente. Es decir, la distribución muestral es bastante amplia. Si replicas un experimento grande y recalculas la muestra, probablemente obtendrás la misma respuesta que obtuviste la última vez, por lo que la distribución del muestreo será muy estrecha. Esto se puede ver visualmente en las Figuras 10.7, 10.8 y 10.9: cuanto mayor es el tamaño de la muestra, más estrecha se vuelve la distribución muestral. Podemos cuantificar este efecto calculando la desviación estándar de la distribución muestral, la cual se conoce como el error estándar. El error estándar de una estadística a menudo se denota SE, y como generalmente nos interesa el error estándar de la media muestral, a menudo usamos el acrónimo SEM. Como puedes ver con solo mirar la imagen, a medida que aumenta el tamaño de muestra N, el SEM disminuye.
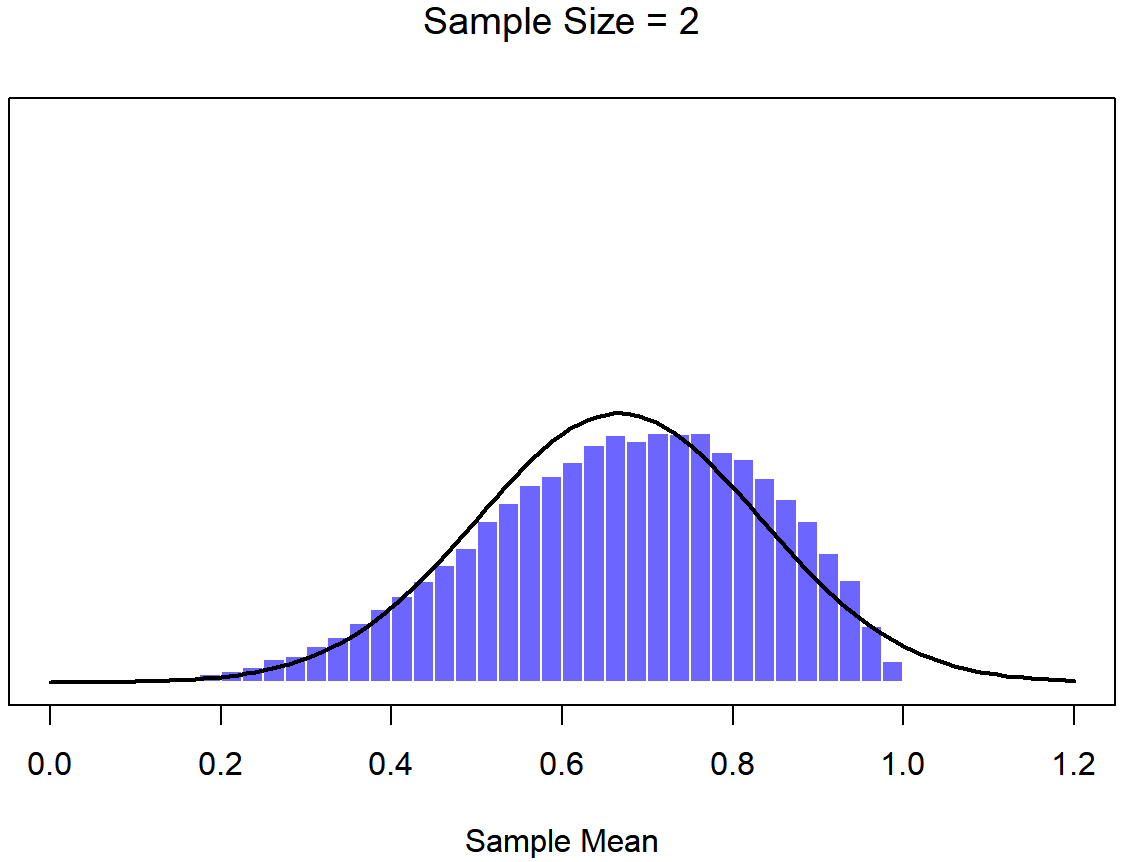
Bien, entonces esa es una parte de la historia. Sin embargo, hay algo que he estado pasando por alto hasta ahora. Todos mis ejemplos hasta este momento se han basado en los experimentos de “puntajes de coeficiente intelectual”, y debido a que los puntajes de CI se distribuyen aproximadamente normalmente, he asumido que la distribución de la población es normal. ¿Y si no es normal? ¿Qué sucede con la distribución muestral de la media? Lo notable es esto: no importa qué forma sea su distribución poblacional, a medida que N aumenta la distribución muestral de la media empieza a parecerse más a una distribución normal. Para darle una idea de esto, hice algunas simulaciones usando R. Para ello, comencé con la distribución “rampada” que se muestra en el histograma de la Figura 10.10. Como puede ver al comparar el histograma de forma triangular con la curva de campana trazada por la línea negra, la distribución de la población no se parece mucho a una distribución normal en absoluto. A continuación, utilicé R para simular los resultados de una gran cantidad de experimentos. En cada experimento tomé N=2 muestras de esta distribución, para luego calcular la media de la muestra. Figura?? traza el histograma de estas medias muestrales (es decir, la distribución muestral de la media para N=2). Esta vez, el histograma produce una distribución en forma de: todavía no es normal, pero está mucho más cerca de la línea negra que la distribución de la población en la Figura? . Cuando aumento el tamaño de la muestra a N=4, la distribución muestral de la media es muy cercana a la normal (Figura?? , y para cuando alcanzamos un tamaño de muestra de N=8 es casi perfectamente normal. En otras palabras, siempre y cuando el tamaño de su muestra no sea pequeño, ¡la distribución muestral de la media será aproximadamente normal sin importar cómo se vea su distribución poblacional!
# needed for printing
width <- 6
height <- 6
# parameters of the beta
a <- 2
b <- 1
# mean and standard deviation of the beta
s <- sqrt( a*b / (a+b)^2 / (a+b+1) )
m <- a / (a+b)
# define function to draw a plot
plotOne <- function(n,N=50000) {
# generate N random sample means of size n
X <- matrix(rbeta(n*N,a,b),n,N)
X <- colMeans(X)
# plot the data
hist( X, breaks=seq(0,1,.025), border="white", freq=FALSE,
col=ifelse(colour,emphColLight,emphGrey),
xlab="Sample Mean", ylab="", xlim=c(0,1.2),
main=paste("Sample Size =",n), axes=FALSE,
font.main=1, ylim=c(0,5)
)
box()
axis(1)
#axis(2)
# plot the theoretical distribution
lines( x <- seq(0,1.2,.01), dnorm(x,m,s/sqrt(n)),
lwd=2, col="black", type="l"
)
}
for( i in c(1,2,4,8)) {
plotOne(i)}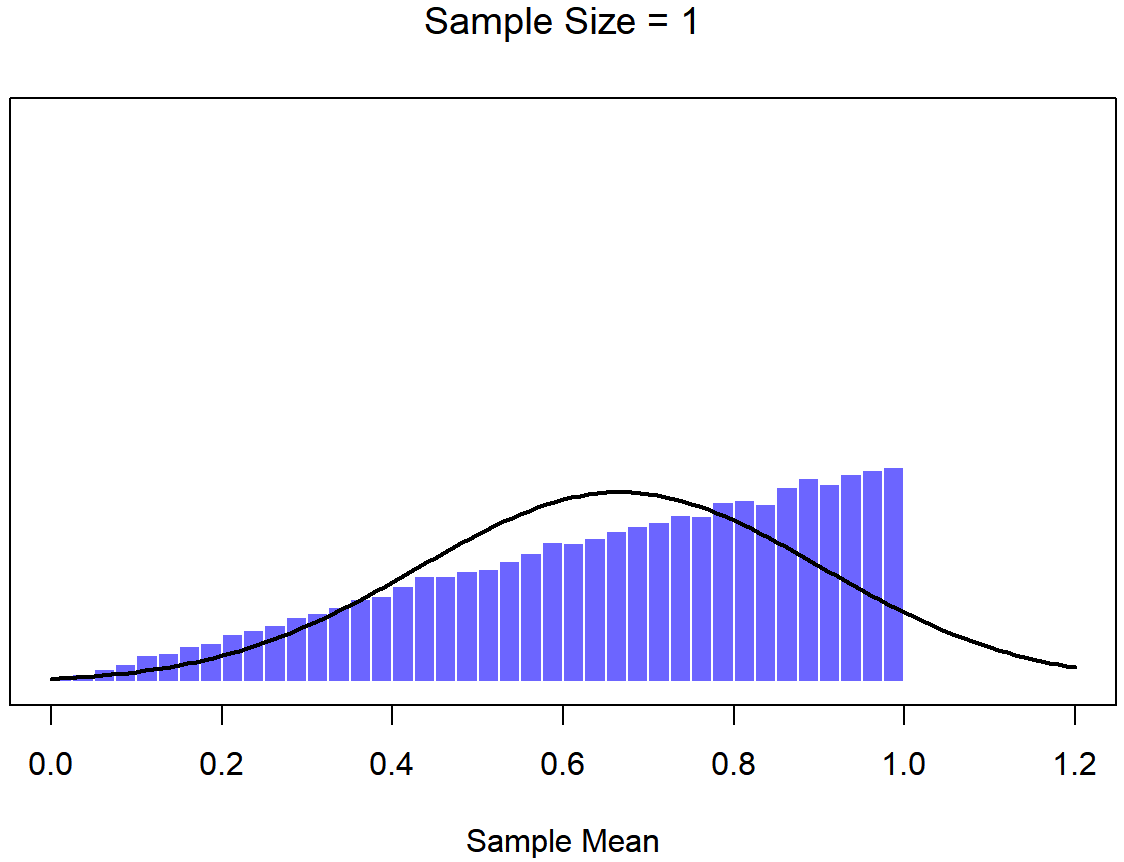
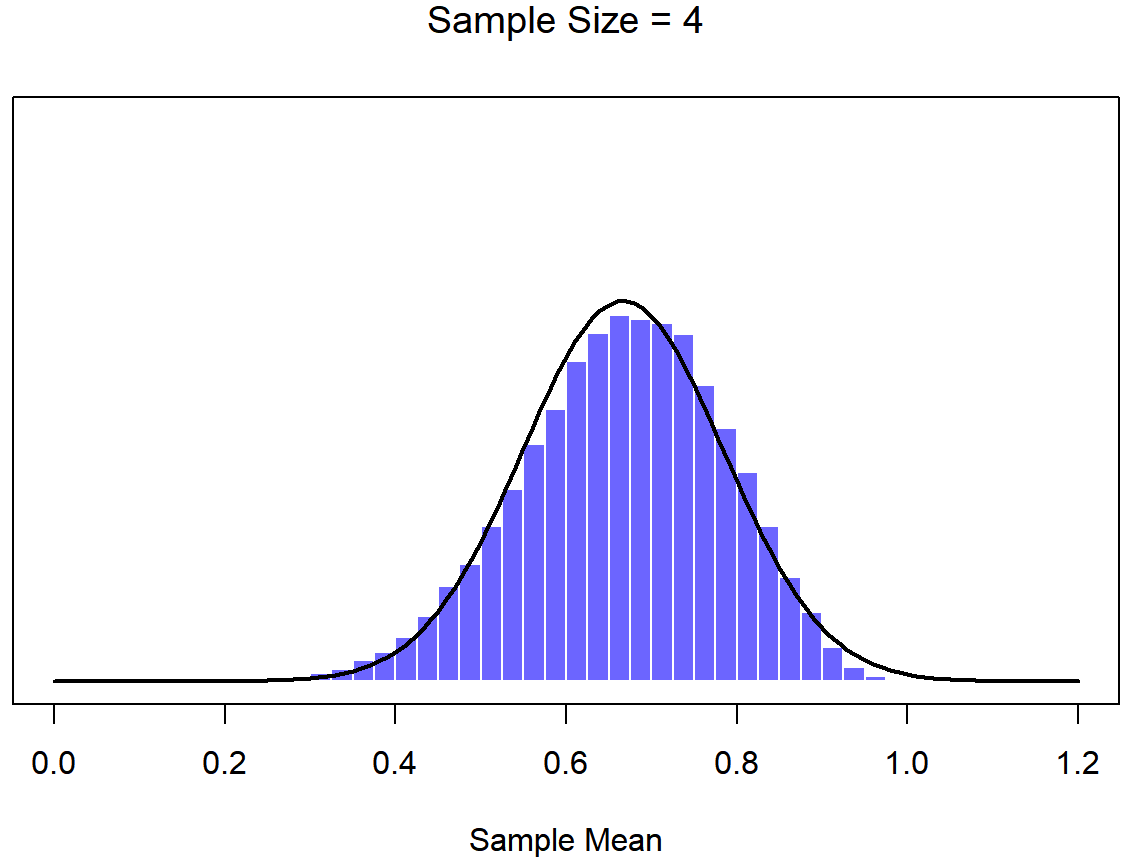
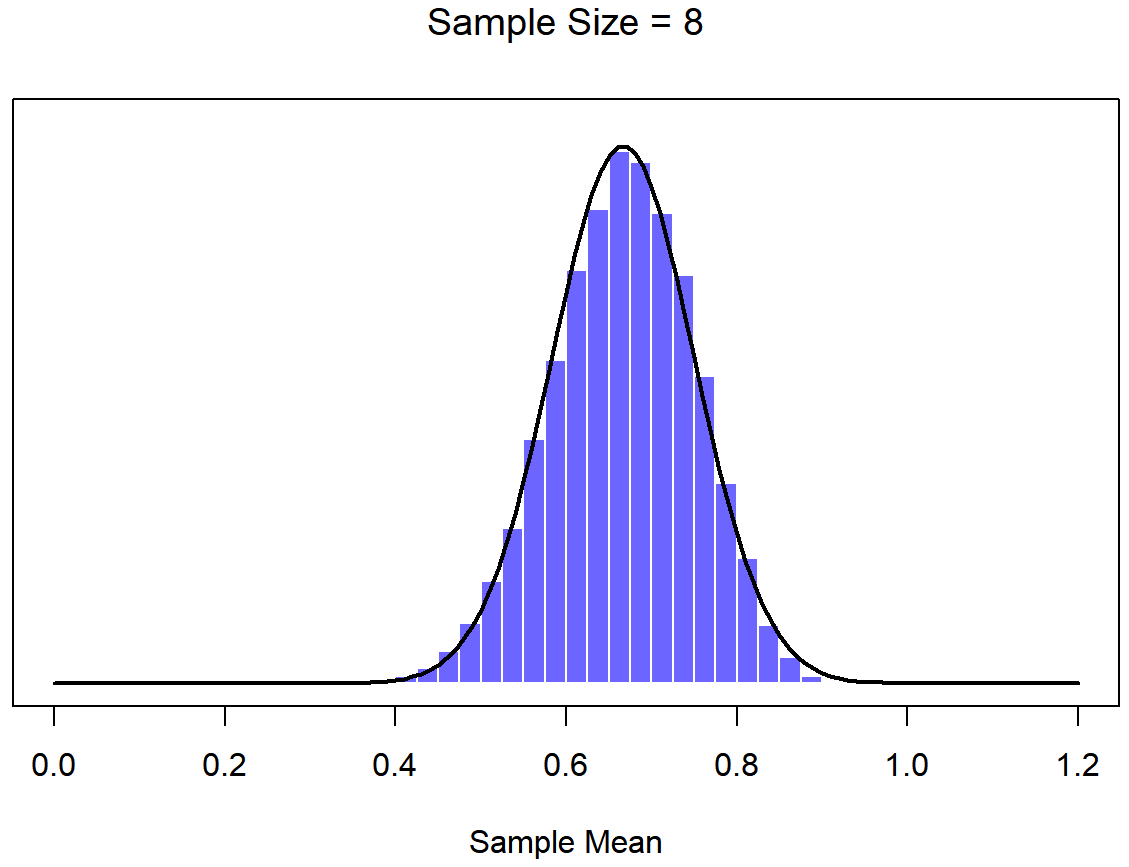
A partir de estas cifras, parece que tenemos evidencia de todas las siguientes afirmaciones sobre la distribución muestral de la media:
- La media de la distribución muestral es la misma que la media de la población
- La desviación estándar de la distribución del muestreo (es decir, el error estándar) se hace más pequeña a medida que aumenta el tamaño de la muestra
- La forma de la distribución del muestreo se vuelve normal a medida que aumenta el tamaño de la muestra
Como sucede, no sólo todas estas afirmaciones son ciertas, hay un teorema muy famoso en la estadística que prueba las tres, conocido como el teorema del límite central. Entre otras cosas, el teorema del límite central nos dice que si la distribución poblacional tiene media μ y desviación estándar σ, entonces la distribución muestral de la media también tiene μ media, y el error estándar de la media es
\ [
\ mathrm {SEM} =\ dfrac {\ sigma} {\ sqrt {N}}
\ nonumber\]
Debido a que dividimos la devación estándar poblacional σ por la raíz cuadrada del tamaño de muestra N, el SEM se hace más pequeño a medida que aumenta el tamaño de la muestra. También nos dice que la forma de la distribución muestral se vuelve normal. 150
Este resultado es útil para todo tipo de cosas. Nos dice por qué los experimentos grandes son más confiables que los pequeños, y debido a que nos da una fórmula explícita para el error estándar nos dice cuánto más confiable es un experimento grande. Nos dice por qué la distribución normal es, bueno, normal. En experimentos reales, muchas de las cosas que queremos medir son en realidad promedios de muchas cantidades diferentes (por ejemplo, posiblemente, la inteligencia “general” medida por el coeficiente intelectual es un promedio de un gran número de habilidades y habilidades “específicas”), y cuando eso sucede, la cantidad promedio debe seguir una normalidad distribución. Debido a esta ley matemática, la distribución normal aparece una y otra vez en datos reales.


