10.4: Estimación de parámetros poblacionales
- Page ID
- 151480
En todos los ejemplos de coeficiente intelectual de las secciones anteriores, en realidad conocíamos los parámetros poblacionales con anticipación. Como cada licenciatura recibe clases en su primera conferencia sobre la medición de la inteligencia, los puntajes de CI se definen para tener media 100 y desviación estándar 15. Sin embargo, esto es un poco mentira. ¿Cómo sabemos que los puntajes de CI tienen una verdadera media poblacional de 100? Bueno, lo sabemos porque las personas que diseñaron las pruebas las han administrado a muestras muy grandes, y luego han “amañado” las reglas de puntuación para que su muestra tenga media de 100. Eso no es malo por supuesto: es una parte importante del diseño de una medición psicológica. Sin embargo, es importante tener en cuenta que esta media teórica de 100 solo se adhiere a la población que los diseñadores de pruebas utilizaron para diseñar las pruebas. Los buenos diseñadores de pruebas harán todo lo posible para proporcionar “normas de prueba” que pueden aplicarse a muchas poblaciones diferentes (por ejemplo, diferentes grupos de edad, nacionalidades, etc.).
Esto es muy útil, pero por supuesto casi todos los proyectos de investigación de interés implican mirar a una población de personas diferente a las utilizadas en las normas de prueba. Por ejemplo, supongamos que desea medir el efecto del envenenamiento por plomo de bajo nivel sobre el funcionamiento cognitivo en Port Pirie, una ciudad industrial del sur de Australia con una fundición de plomo. Quizás decidas que quieres comparar los puntajes de coeficiente intelectual entre personas en Port Pirie con una muestra comparable en Whyalla, una ciudad industrial del sur de Australia con una refinería de acero. 151 Independientemente de en qué ciudad estés pensando, no tiene mucho sentido simplemente asumir que el verdadero coeficiente intelectual medio de la población es de 100. Nadie ha producido, que yo sepa, datos de normalización sensatos que puedan aplicarse automáticamente a las ciudades industriales de Australia del Sur. Vamos a tener que estimar los parámetros poblacionales a partir de una muestra de datos. Entonces, ¿cómo hacemos esto?
Estimación de la media poblacional
Supongamos que vamos a Port Pirie y 100 de los lugareños tienen la amabilidad de sentarse a través de una prueba de CI. El puntaje promedio de CI entre estas personas resulta ser\(\bar{X}\) =98.5. Entonces, ¿cuál es el verdadero coeficiente intelectual medio para toda la población de Port Pirie? Obviamente, no sabemos la respuesta a esa pregunta. Podría ser 97.2, pero si también podría ser 103.5. Nuestro muestreo no es exhaustivo por lo que no podemos dar una respuesta definitiva. Sin embargo, si me obligaron a punta de pistola a dar una “mejor suposición” tendría que decir 98.5. Esa es la esencia de la estimación estadística: dar una mejor suposición.
En este ejemplo, estimar el parámetro de poulación desconocido es sencillo. Calculo la media muestral, y la uso como mi estimación de la media poblacional. Es bastante simple, y en la siguiente sección voy a explicar la justificación estadística de esta respuesta intuitiva. No obstante, por el momento lo que quiero hacer es asegurarme de que reconozcas que el estadístico muestral y la estimación del parámetro poblacional son cosas conceptualmente diferentes. Un estadístico de muestra es una descripción de sus datos, mientras que la estimación es una suposición sobre la población. Con eso en mente, los estadísticos suelen tener notación diferente para referirse a ellos. Por ejemplo, si la verdadera media poblacional se denota μ, entonces usaríamos\(\hat{\mu}\) para referirnos a nuestra estimación de la media poblacional. En contraste, la media muestral se denota\(\bar{X}\) o a veces m. Sin embargo, en muestras simples aleatorias, la estimación de la media poblacional es idéntica a la media muestral: si observo una media muestral de\(\bar{X}\) =98.5, entonces mi estimación de la media poblacional también es\(\hat{\mu}\) =98.5. Para ayudar a mantener la notación clara, aquí hay una tabla práctica:
knitr::kable(data.frame(stringsAsFactors=FALSE,
Symbol = c("$\\bar{X}$", "$\\mu$", "$\\hat{\\mu}$"),
What.is.it = c("Sample mean", "True population mean",
"Estimate of the population mean"),
Do.we.know.what.it.is = c("Yes calculated from the raw data",
"Almost never known for sure",
"Yes identical to the sample mean")))| Símbolo | What.is.it | Do.sabemos.what.it.is |
|---|---|---|
| \(\bar{X}\) | Media de la muestra | Sí calculado a partir de los datos brutos |
| μ | Media verdadera de la población | Casi nunca se sabe con certeza |
| \(\hat{\mu}\) | Estimación de la media poblacional | Sí idéntico a la media de la muestra |
Estimación de la desviación estándar de la población
Hasta ahora, la estimación parece bastante simple, y quizás te estés preguntando por qué te obligué a leer todas esas cosas sobre la teoría del muestreo. En el caso de la media, nuestra estimación del parámetro poblacional (i.e.\(\hat{\mu}\)) resultó ser idéntica a la estadística muestral correspondiente (i.e.\(\bar{X}\)). Sin embargo, eso no siempre es cierto. Para ver esto, pensemos cómo construir una estimación de la desviación estándar de la población, que vamos a denotar\(\hat{\sigma}\). ¿Cuál vamos a utilizar como estimación en este caso? Tu primer pensamiento podría ser que podríamos hacer lo mismo que hicimos al estimar la media, y simplemente usar el estadístico de muestra como nuestra estimación. Eso es casi lo correcto, pero no del todo.
He aquí por qué. Supongamos que tengo una muestra que contiene una sola observación. Para este ejemplo, ayuda considerar una muestra donde no se tienen intuciones en absoluto sobre cuáles podrían ser los verdaderos valores de la población, así que usemos algo completamente ficticio. Supongamos que la observación en cuestión mide la cromulencia de mis zapatos. Resulta que mis zapatos tienen una cromulencia de 20. Así que aquí está mi muestra:
20Esta es una muestra perfectamente legítima, aunque tenga un tamaño de muestra de N=1. Tiene una media muestral de 20, y porque cada observación en esta muestra es igual a la media muestral (¡obviamente!) tiene una desviación estándar muestral de 0. Como descripción de la muestra esto parece bastante correcto: la muestra contiene una sola observación y por lo tanto no se observa variación dentro de la muestra. Una desviación estándar muestral de s=0 es la respuesta correcta aquí. Pero como estimación de la desviación estándar de la población, se siente completamente demente, ¿verdad? Es cierto que tú y yo no sabemos nada sobre lo que es la “cromulencia”, pero sabemos algo sobre los datos: ¡la única razón por la que no vemos ninguna variabilidad en la muestra es que la muestra es demasiado pequeña para mostrar alguna variación! Entonces, si tienes un tamaño de muestra de N=1, parece que la respuesta correcta es solo decir “ni idea”.
Observe que no tiene la misma intuición cuando se trata de la media muestral y la media poblacional. Si se ve obligado a hacer una mejor conjetura sobre la media poblacional, no se siente completamente demente adivinar que la media poblacional es 20. Seguro, probablemente no te sentirías muy confiado en esa suposición, porque solo tienes la única observación con la que trabajar, pero sigue siendo la mejor conjetura que puedes hacer.
Extendamos un poco este ejemplo. Supongamos que ahora hago una segunda observación. Mi conjunto de datos ahora tiene N=2 observaciones de la cromulencia de los zapatos, y la muestra completa ahora se ve así:
20, 22En esta ocasión, nuestra muestra es lo suficientemente grande como para que podamos observar alguna variabilidad: ¡dos observaciones es el número mínimo necesario para que se observe cualquier variabilidad! Para nuestro nuevo conjunto de datos, la media muestral es\(\bar{X}\) =21, y la desviación estándar muestral es s=1. ¿Qué intuiciones tenemos sobre la población? Nuevamente, en lo que respecta a la media poblacional, la mejor conjetura que podemos hacer es la media muestral: si se obliga a adivinar, probablemente adivinaríamos que la cromulencia media poblacional es 21. ¿Qué pasa con la desviación estándar? Esto es un poco más complicado. La desviación estándar de la muestra se basa únicamente en dos observaciones, y si eres como yo probablemente tengas la intuición de que, con solo dos observaciones, no le hemos dado a la población “suficientes oportunidades” para revelarnos su verdadera variabilidad. No es sólo que sospechemos que la estimación es incorrecta: después de todo, con sólo dos observaciones esperamos que esté equivocada hasta cierto punto. La preocupación es que el error sea sistemático. Específicamente, sospechamos que la desviación estándar de la muestra probablemente sea menor que la desviación estándar de la población.
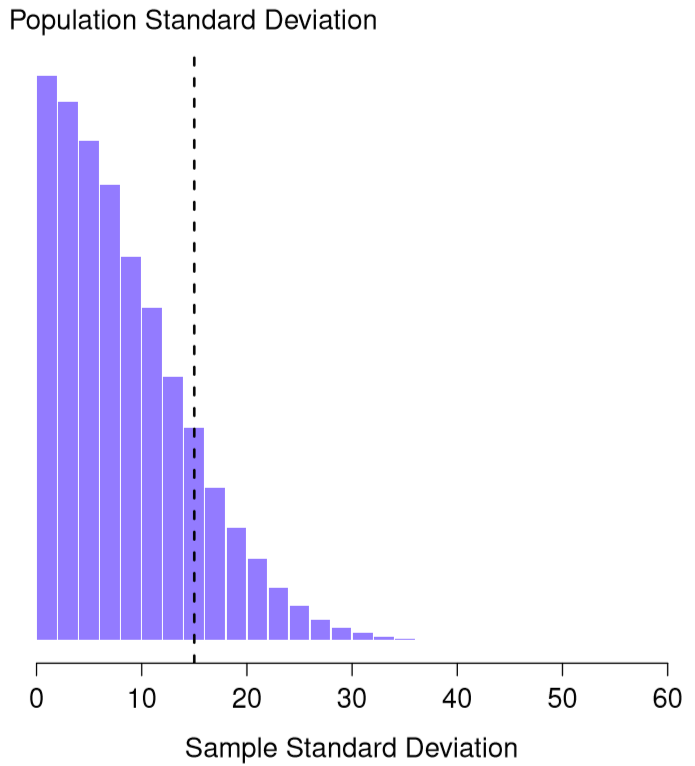
Esta intuición se siente bien, pero sería bueno demostrarlo de alguna manera. De hecho hay pruebas matemáticas que confirman esta intuición, pero a menos que tengas los antecedentes matemáticos adecuados no ayudan mucho. En cambio, lo que voy a hacer es usar R para simular los resultados de algunos experimentos. Con eso en mente, volvamos a nuestros estudios de CI. Supongamos que el coeficiente intelectual medio poblacional verdadero es 100 y la desviación estándar es 15. Puedo usar la función rnorm () para generar los resultados de un experimento en el que mido N=2 IQ scores, y calcular la desviación estándar de la muestra. Si hago esto una y otra vez, y trazo un histograma de estas desviaciones estándar de muestra, lo que tengo es la distribución muestral de la desviación estándar. He trazado esta distribución en la Figura 10.11. A pesar de que la verdadera desviación estándar de la población es de 15, el promedio de las desviaciones estándar de la muestra es de sólo 8.5. Observe que este es un resultado muy diferente al que encontramos en la Figura 10.8 cuando trazamos la distribución muestral de la media. Si miras esa distribución muestral, lo que ves es que la media poblacional es 100, y el promedio de las medias muestrales también es 100.
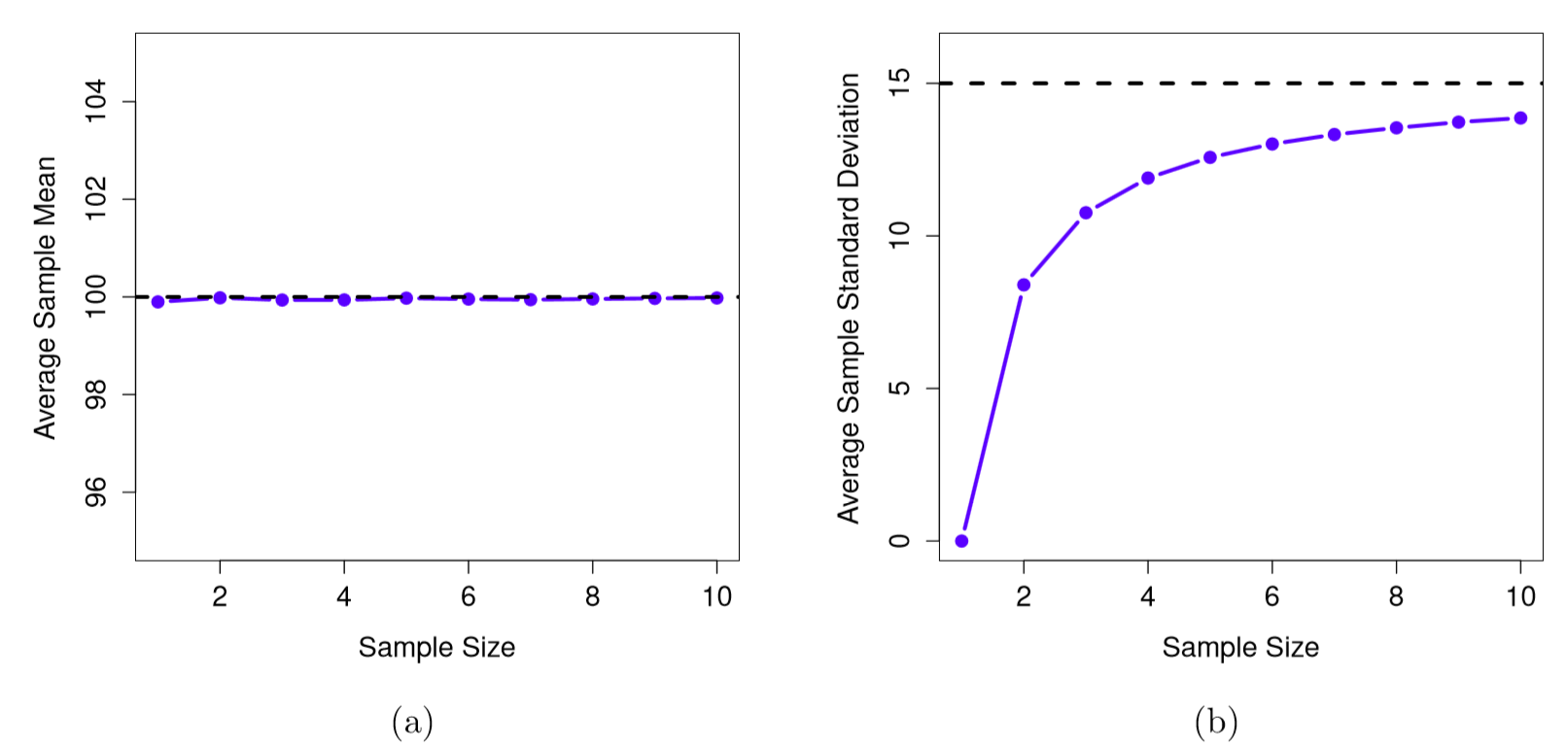
Ahora vamos a extender la simulación. En lugar de restringirnos a la situación en la que tenemos un tamaño de muestra de N=2, repitamos el ejercicio para tamaños de muestra del 1 al 10. Si trazamos la media muestral promedio y la desviación estándar promedio de la muestra en función del tamaño de la muestra, se obtienen los resultados que se muestran en la Figura 10.12. En el lado izquierdo (panel a), he trazado la media promedio de la muestra y en el lado derecho (panel b), he trazado la desviación estándar promedio. Las dos parcelas son bastante diferentes: en promedio, la media muestral promedio es igual a la media poblacional. Se trata de un estimador imparcial, que es esencialmente la razón por la que tu mejor estimación para la media poblacional es la media muestral. 152 La parcela de la derecha es bastante diferente: en promedio, la desviación estándar muestral s es menor que la desviación estándar poblacional σ. Es un estimador sesgado. En otras palabras, si queremos hacer una “mejor conjetura”\(\hat{\sigma}\) sobre el valor de la desviación estándar poblacional σ, debemos asegurarnos de que nuestra conjetura sea un poco mayor que la desviación estándar de la muestra s.
La solución a este sesgo sistemático resulta muy simple. Así es como funciona. Antes de abordar la desviación estándar, veamos la varianza. Si recuerda de la Sección 5.2, la varianza de la muestra se define como el promedio de las desviaciones cuadradas de la media de la muestra. Es decir:
\(s^{2}=\dfrac{1}{N} \sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2}\)
La varianza muestral s 2 es un estimador sesgado de la varianza poblacional σ 2. Pero resulta que solo necesitamos hacer un pequeño retoque para transformar esto en un estimador imparcial. Todo lo que tenemos que hacer es dividir por N−1 en lugar de por N. Si hacemos eso, obtenemos la siguiente fórmula:
\(\hat{\sigma}\ ^{2}=\dfrac{1}{N-1} \sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2}\)
Este es un estimador imparcial de la varianza poblacional σ. Además, esto finalmente responde a la pregunta que planteamos en la Sección 5.2. ¿Por qué R nos dio respuestas ligeramente diferentes cuando usamos la función var ()? Porque la función var () calcula\(\hat{\sigma}\ ^{2}\) no s 2, por eso. Una historia similar se aplica para la desviación estándar. Si dividimos por N−1 en lugar de N, nuestra estimación de la desviación estándar poblacional se convierte en:
\(\hat{\sigma}=\sqrt{\dfrac{1}{N-1} \sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2}}\)
y cuando usamos R's construido en función de desviación estándar sd (), lo que está haciendo es calcular\(\hat{σ}\), no s. 153
Un punto final: en la práctica, mucha gente tiende a referirse a\(\hat{σ}\) (es decir, la fórmula donde dividimos por N−1) como la desviación estándar de la muestra. Técnicamente, esto es incorrecto: la desviación estándar de la muestra debe ser igual a s (es decir, la fórmula donde dividimos por N). No son lo mismo, ni conceptual ni numéricamente. Una es propiedad de la muestra, la otra es una característica estimada de la población. Sin embargo, en casi todas las aplicaciones de la vida real, lo que realmente nos importa es la estimación del parámetro poblacional, y así la gente siempre informa en\(\hat{σ}\) lugar de s. Este es el número correcto para informar, por supuesto, es que las personas tienden a ponerse un poco imprecisas sobre la terminología cuando la escriben , porque la “desviación estándar de la muestra” es más corta que la “desviación estándar estimada de la población”. No es gran cosa, y en la práctica hago lo mismo que hacen todos los demás. No obstante, creo que es importante mantener separados los dos conceptos: nunca es buena idea confundir “propiedades conocidas de tu muestra” con “conjeturas sobre la población de la que procede”. En el momento en que empiezas a pensar que es y\(\hat{σ}\) son lo mismo, empiezas a hacer exactamente eso.
Para terminar esta sección, aquí hay otro par de tablas para ayudar a mantener las cosas claras:
knitr::kable(data.frame(stringsAsFactors=FALSE,
Symbol = c("$s$", "$\\sigma$", "$\\hat{\\sigma}$", "$s^2$",
"$\\sigma^2$", "$\\hat{\\sigma}^2$"),
What.is.it = c("Sample standard deviation",
"Population standard deviation",
"Estimate of the population standard deviation", "Sample variance",
"Population variance",
"Estimate of the population variance"),
Do.we.know.what.it.is = c("Yes - calculated from the raw data",
"Almost never known for sure",
"Yes - but not the same as the sample standard deviation",
"Yes - calculated from the raw data",
"Almost never known for sure",
"Yes - but not the same as the sample variance")
))| Símbolo | What.is.it | Do.sabemos.what.it.is |
|---|---|---|
| s | Desviación estándar de muestra | Sí - calculado a partir de los datos brutos |
| σ | Desviación estándar poblacional | Casi nunca se sabe con certeza |
| \(\hat{σ}\) | Estimación de la desviación estándar de la población | Sí, pero no lo mismo que la desviación estándar de la muestra |
| s 2 | Varianza de la muestra | Sí - calculado a partir de los datos brutos |
| σ 2 | Varianza poblacional | Casi nunca se sabe con certeza |
| \(\hat{\sigma}\ ^{2}\) | Estimación de la varianza poblacional | Sí, pero no lo mismo que la varianza de la muestra |


