13.9: Comprobación de la normalidad de una muestra
- Page ID
- 151832
Todas las pruebas que hemos discutido hasta ahora en este capítulo han asumido que los datos se distribuyen normalmente. Esta suposición suele ser bastante razonable, porque el teorema del límite central (Sección 10.3.3) tiende a asegurar que muchas cantidades del mundo real se distribuyen normalmente: cada vez que sospechas que tu variable es en realidad un promedio de muchas cosas diferentes, hay una bonita buena probabilidad de que se distribuya normalmente; o al menos lo suficientemente cerca de lo normal como para que puedas salirte con la tuya usando pruebas t. Sin embargo, la vida no viene con garantías; y además, hay muchas maneras en las que puedes terminar con variables que son altamente no normales. Por ejemplo, cada vez que piensas que tu variable es en realidad el mínimo de muchas cosas diferentes, hay muy buenas posibilidades de que termine bastante sesgada. En psicología, los datos de tiempo de respuesta (RT) son un buen ejemplo de ello. Si suponemos que hay muchas cosas que podrían desencadenar una respuesta de un participante humano, entonces la respuesta real ocurrirá la primera vez que ocurra uno de estos eventos desencadenantes. 198 Esto significa que los datos de RT son sistemáticamente no normales. Bien, entonces si la normalidad es asumida por todas las pruebas, y en su mayoría pero no siempre está satisfecha (al menos aproximadamente) por los datos del mundo real, ¿cómo podemos verificar la normalidad de una muestra? En esta sección discuto dos métodos: las gráficas QQ y la prueba de Shapiro-Wilk.
parcelas
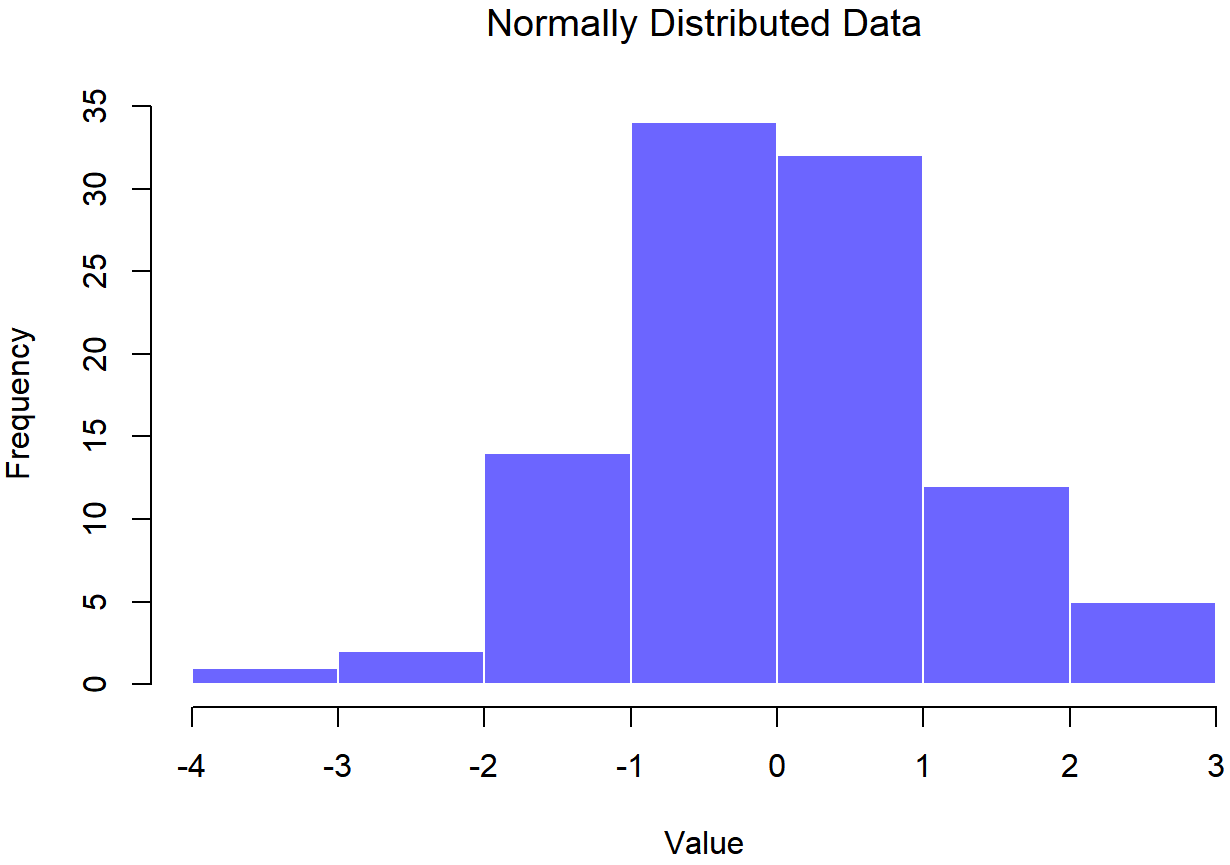
normal.data, una muestra normalmente distribuida con 100 observaciones.## Normally Distributed Data
## skew= -0.02936155
## kurtosis= -0.06035938
##
## Shapiro-Wilk normality test
##
## data: data
## W = 0.99108, p-value = 0.7515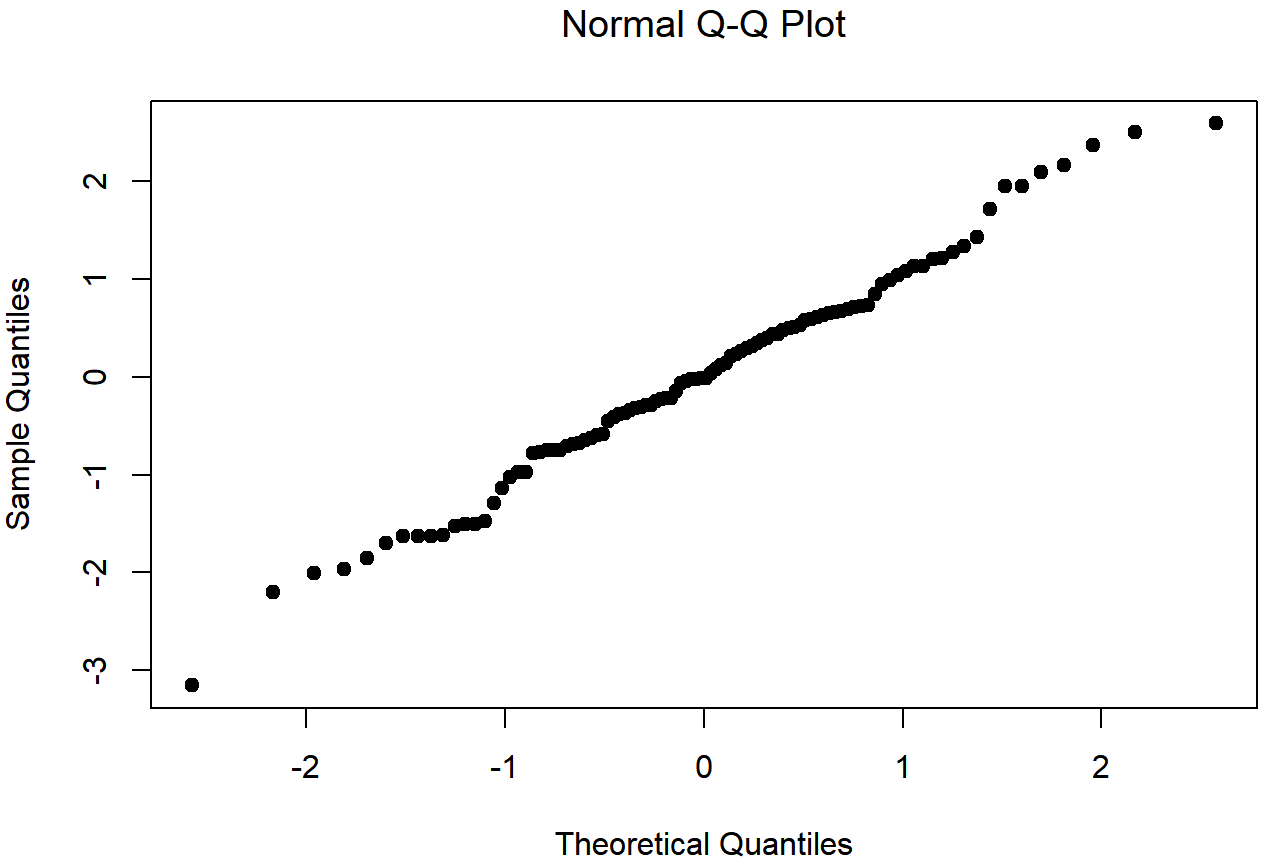
normal.data, una muestra normalmente distribuida con 100 observaciones.El estadístico Shapiro-Wilk asociado a los datos de las Figuras 13.14 y 13.15 es W=.99, lo que indica que no se detectaron desviaciones significativas de la normalidad (p=.73). Como puedes ver, estos datos forman una línea bastante recta; ¡lo cual no es de sorprender dado que los muestreamos de una distribución normal! En contraste, eche un vistazo a los dos conjuntos de datos que se muestran en las Figuras 13.16, 13.17, 13.18, 13.19. Las figuras 13.16 y 13.17 muestran el histograma y una gráfica QQ para un conjunto de datos altamente sesgado: la gráfica QQ se curva hacia arriba. Las figuras 13.18 y 13.19 muestran las mismas gráficas para un conjunto de datos de cola pesada (es decir, alta curtosis): en este caso, la gráfica QQ se aplana en el medio y se curva bruscamente en cada extremo.
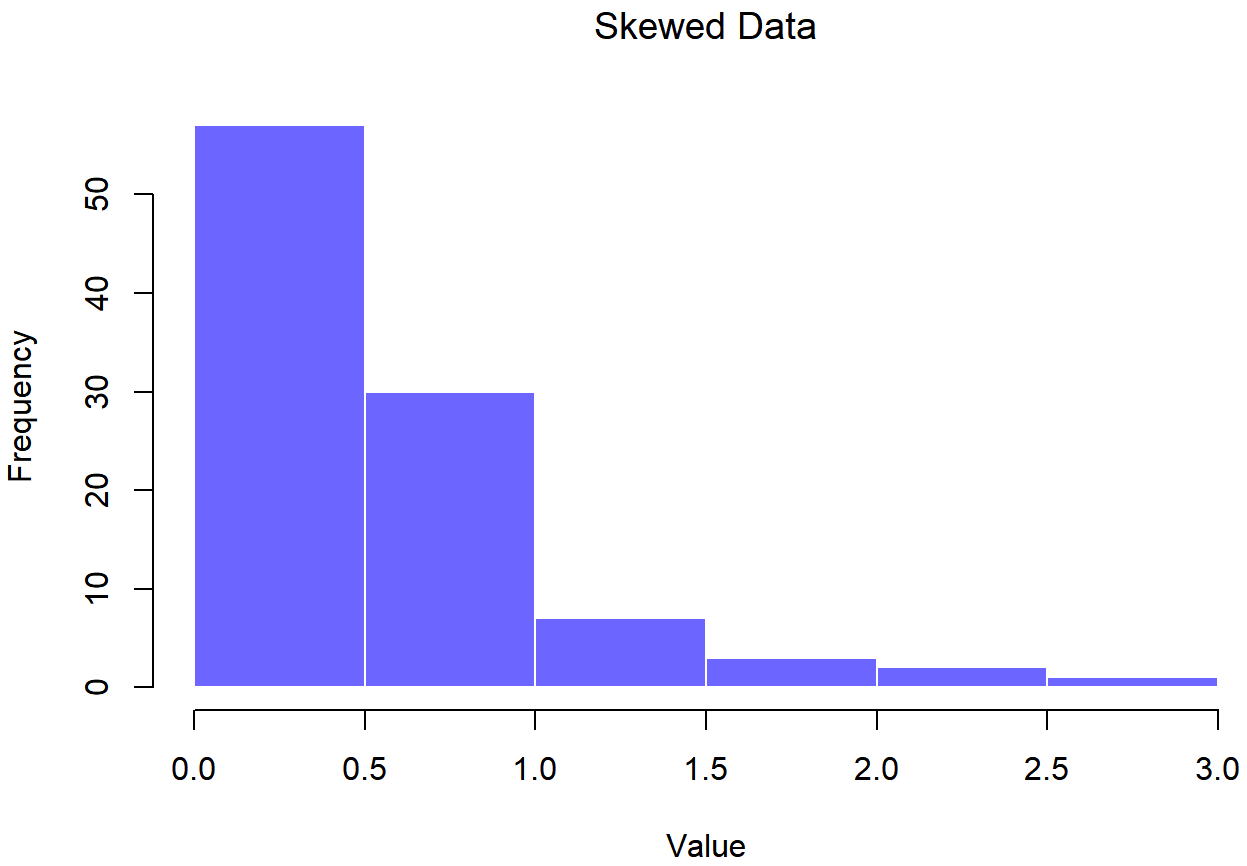
de datos sesgados## Skewed Data
## skew= 1.889475
## kurtosis= 4.4396
##
## Shapiro-Wilk normality test
##
## data: data
## W = 0.81758, p-value = 8.908e-10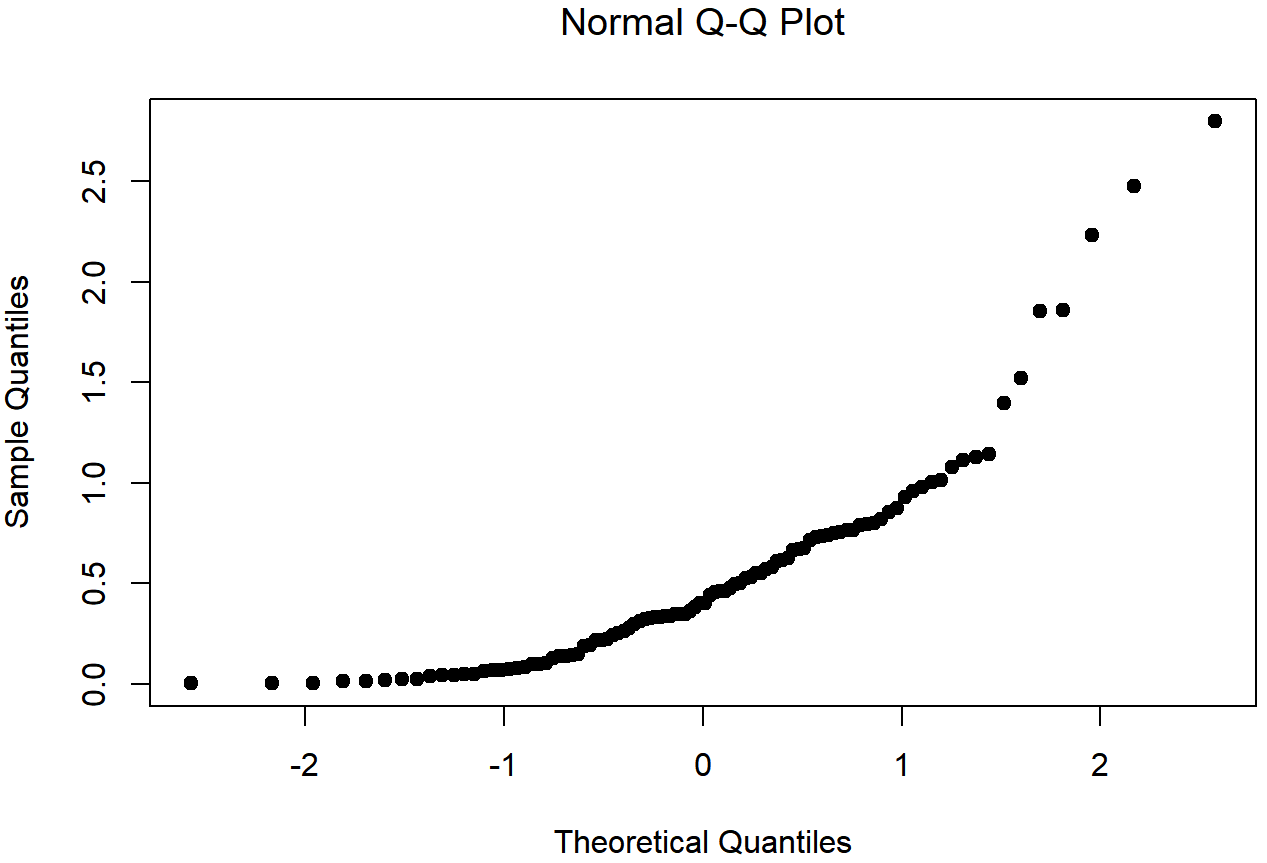
de datos sesgadosLa asimetría de los datos en las Figuras 13.16 y 13.17 es de 1.94, y se refleja en una gráfica QQ que se curva hacia arriba. Como consecuencia, el estadístico Shapiro-Wilk es W=.80, reflejando una desviación significativa de la normalidad (p<.001).
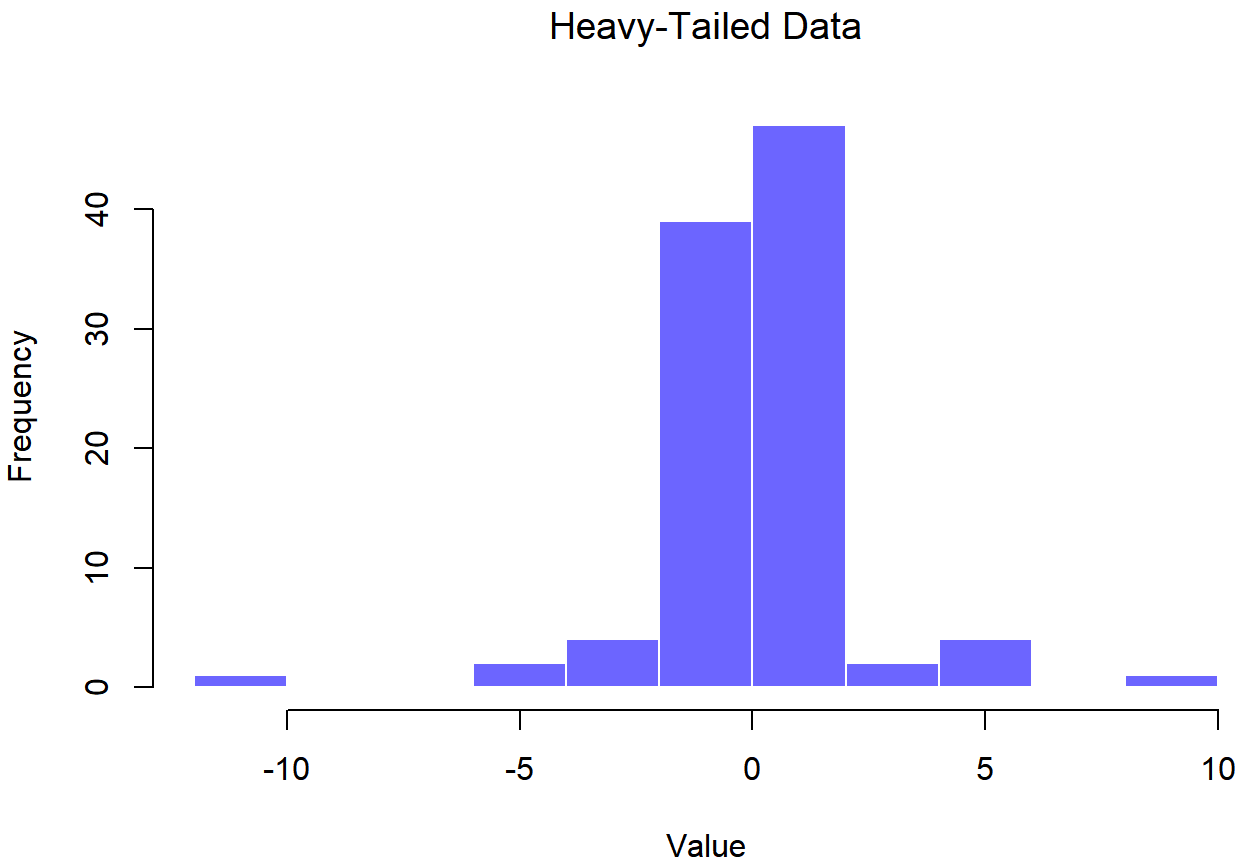
## Heavy-Tailed Data
## skew= -0.05308273
## kurtosis= 7.508765
##
## Shapiro-Wilk normality test
##
## data: data
## W = 0.83892, p-value = 4.718e-09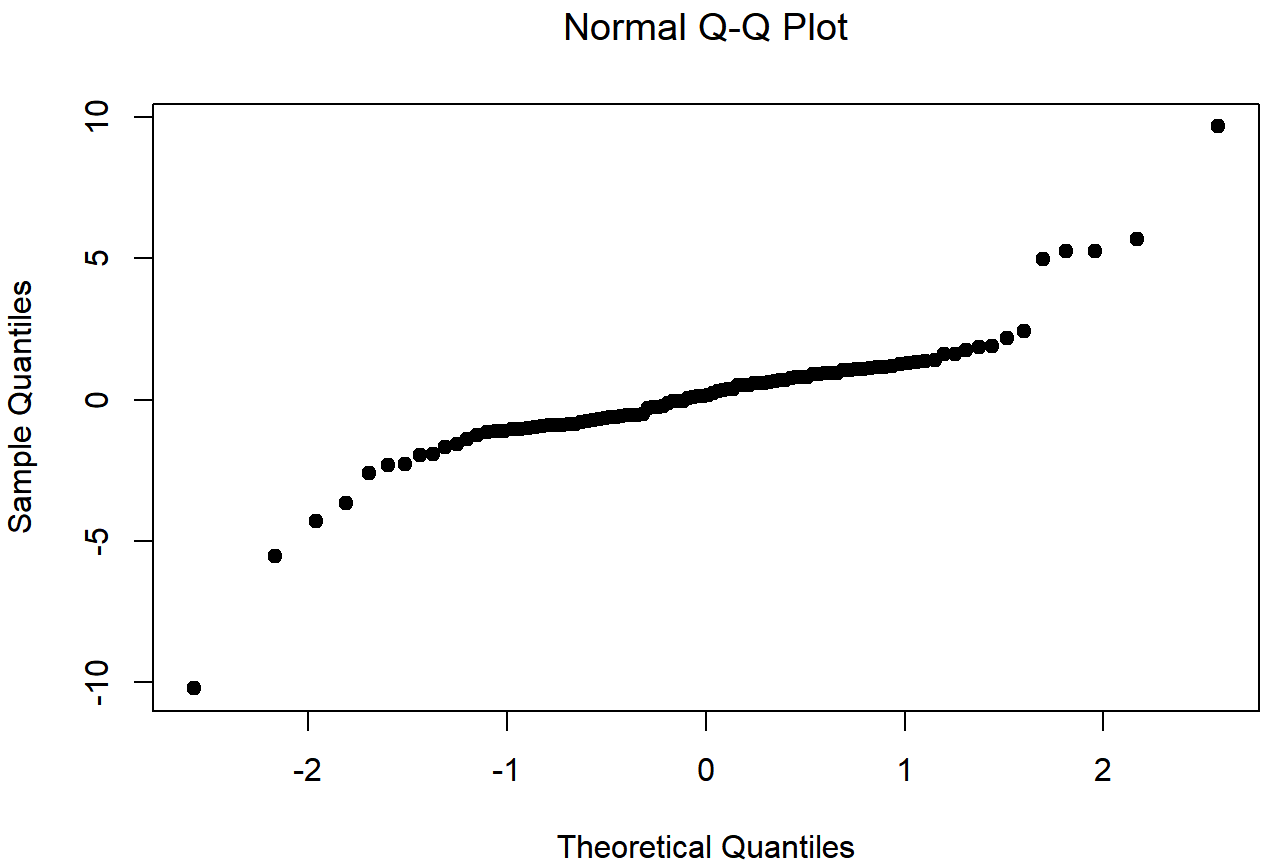
Las figuras 13.18 y 13.19 muestran las mismas gráficas para un conjunto de datos de cola pesada, que nuevamente consta de 100 observaciones. En este caso, las colas pesadas en los datos producen una curtosis alta (2.80), y hacen que la gráfica QQ se aplane en el medio, y se curve bruscamente a ambos lados. El estadístico Shapiro-Wilk resultante es W=.93, reflejando nuevamente una falta de normalidad significativa (p<.001).
Una forma de verificar si una muestra viola el supuesto de normalidad es dibujar una gráfica “cuantil-cuantil” (gráfica QQ). Esto le permite verificar visualmente si está viendo alguna violación sistemática. En una gráfica QQ, cada observación se traza como un solo punto. La coordenada x es el cuantil teórico en el que debe caer la observación, si los datos se distribuyeron normalmente (con media y varianza estimada a partir de la muestra) y en la coordenada y está el cuantil real de los datos dentro de la muestra. Si los datos son normales, los puntos deben formar una línea recta. Por ejemplo, veamos qué sucede si generamos datos por muestreo a partir de una distribución normal, y luego dibujamos una gráfica QQ usando la función R qqnorm (). La función qqnorm () tiene algunos argumentos, pero el único que realmente necesitamos preocuparnos aquí es y, un vector que especifica los datos cuya normalidad nos interesa verificar. Aquí están los comandos R:
normal.data <- rnorm( n = 100 ) # generate N = 100 normally distributed numbers
hist( x = normal.data ) # draw a histogram of these numbers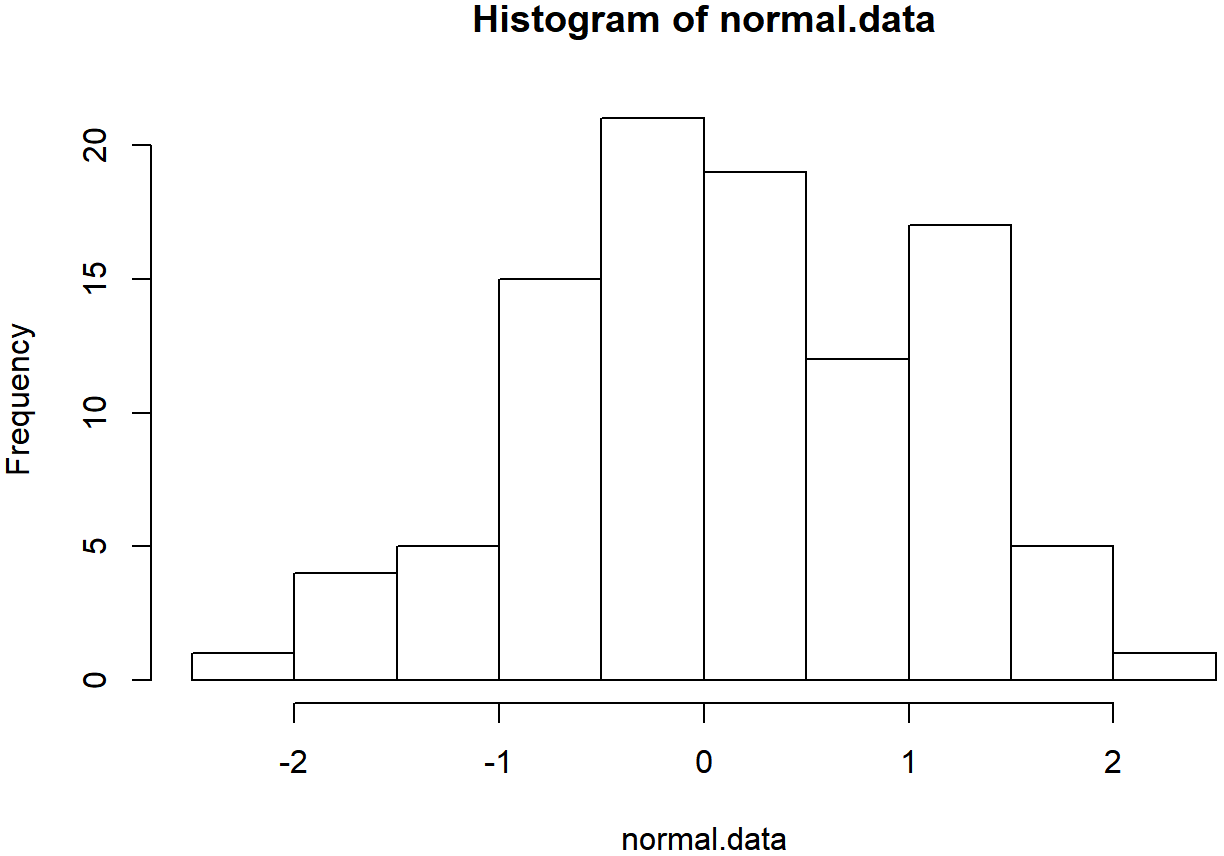
qqnorm( y = normal.data ) # draw the QQ plot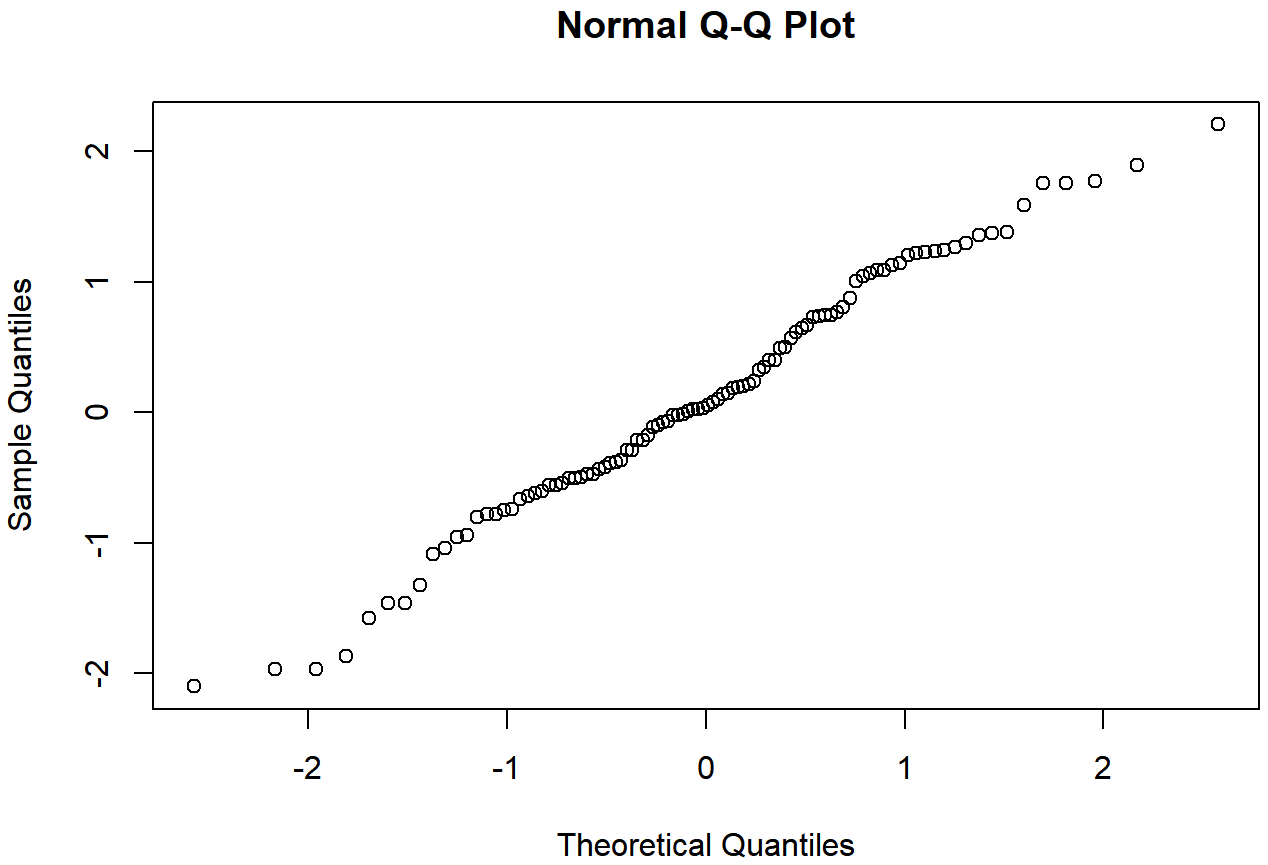
Pruebas Shapiro-Wilk
Aunque las parcelas QQ proporcionan una buena manera de verificar informalmente la normalidad de tus datos, a veces querrás hacer algo un poco más formal. Y cuando llegue ese momento, la prueba Shapiro-Wilk (Shapiro y Wilk 1965) es probablemente lo que estás buscando. 199 Como era de esperar, la hipótesis nula que se está probando es que normalmente se distribuye un conjunto de N observaciones. El estadístico de prueba que calcula se denota convencionalmente como W, y se calcula de la siguiente manera. Primero, ordenamos las observaciones en orden de aumento de tamaño, y dejamos que X1 sea el valor más pequeño en la muestra, X2 sea el segundo más pequeño y así sucesivamente. Entonces el valor de W viene dado por
\(W=\dfrac{\left(\sum_{i=1}^{N} a_{i} X_{i}\right)^{2}}{\sum_{i=1}^{N}\left(X_{i}-\bar{X}\right)^{2}}\)
donde\(\ \bar{X}\) está la media de las observaciones, y los valores de ai son... murmurar, murmurar... algo complicado que está un poco más allá del alcance de un texto introductorio.
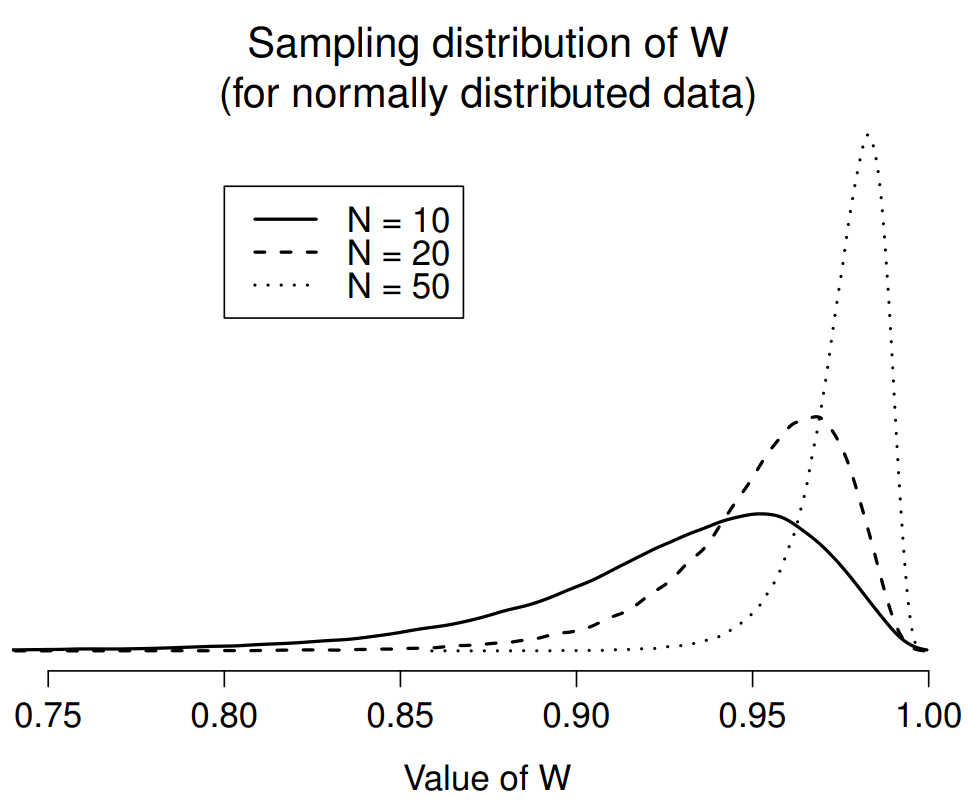
Debido a que es un poco difícil explicar las matemáticas detrás de la estadística W, una mejor idea es dar una descripción amplia de cómo se comporta. A diferencia de la mayoría de las estadísticas de prueba que encontraremos en este libro, en realidad son pequeños valores de W los que indicaban desviación de la normalidad. El estadístico W tiene un valor máximo de 1, que surge cuando los datos se ven “perfectamente normales”. Cuanto menor es el valor de W, menos normales son los datos. Sin embargo, la distribución de muestreo para W —que no es una de las estándar que discutí en el Capítulo 9 y de hecho es un completo dolor en el culo para trabajar— sí depende del tamaño de muestra N. Para darle una idea de cómo son estas distribuciones de muestreo, he trazado tres de ellas en la Figura 13.20. Observe que, a medida que el tamaño de la muestra comienza a ser grande, la distribución de muestreo se agrupa muy estrechamente cerca de W=1, y como consecuencia, para muestras más grandes, W no tiene que ser mucho menor que 1 para que la prueba sea significativa.
Para ejecutar la prueba en R, utilizamos la función shapiro.test (). Tiene sólo un único argumento x, que es un vector numérico que contiene los datos cuya normalidad necesita ser probada. Por ejemplo, cuando aplicamos esta función a nuestro normal.data, obtenemos lo siguiente:
shapiro.test( x = normal.data )##
## Shapiro-Wilk normality test
##
## data: normal.data
## W = 0.98654, p-value = 0.4076Entonces, no es sorprendente, no tenemos evidencia de que estos datos se aparten de la normalidad. Al informar los resultados para una prueba Shapiro-Wilk, debe (como de costumbre) asegurarse de incluir el estadístico de prueba W y el valor p, aunque dado que la distribución del muestreo depende tanto de N, probablemente sería una cortesía incluir también N.


