13.10: Prueba de datos no normales con pruebas de Wilcoxon
- Page ID
- 151802
Bien, supongamos que tus datos resultan ser bastante sustancialmente no normales, pero ¿aún quieres ejecutar algo así como una prueba t? Esta situación se da mucho en la vida real: para los datos de márgenes ganadores de la AFL, por ejemplo, la prueba Shapiro-Wilk dejó muy claro que se viola el supuesto de normalidad. Esta es la situación en la que quieres usar las pruebas de Wilcoxon.
Al igual que la prueba t, la prueba de Wilcoxon viene en dos formas, una muestra y dos muestras, y se utilizan en más o menos las mismas situaciones exactas que las pruebas t correspondientes. A diferencia de la prueba t, la prueba de Wilcoxon no asume normalidad, lo cual es agradable. De hecho, no hacen suposiciones sobre qué tipo de distribución está involucrada: en la jerga estadística, esto los convierte en pruebas no paramétricas. Si bien es agradable evitar la suposición de normalidad, hay un inconveniente: la prueba de Wilcoxon suele ser menos potente que la prueba t (es decir, mayor tasa de error Tipo II). No voy a discutir las pruebas de Wilcoxon con tanto detalle como las pruebas t, pero les voy a dar un breve resumen.
muestra de prueba de Wilcoxon
Comenzaré describiendo la prueba de dos muestras de Wilcoxon (también conocida como la prueba de Mann-Whitney), ya que en realidad es más simple que la versión de una muestra. Supongamos que estamos viendo los puntajes de 10 personas en alguna prueba. Como mi imaginación ahora me ha fallado por completo, pretendamos que es una “prueba de asombro”, y hay dos grupos de personas, “A” y “B”. Tengo curiosidad por saber qué grupo es más impresionante. Los datos están incluidos en el archivo awesome.rdata, y como muchos de los conjuntos de datos que he estado usando, contiene solo un solo marco de datos, en este caso llamado awesome. Aquí están los datos:
load("./rbook-master/data/awesome.Rdata")
print( awesome )## scores group
## 1 6.4 A
## 2 10.7 A
## 3 11.9 A
## 4 7.3 A
## 5 10.0 A
## 6 14.5 B
## 7 10.4 B
## 8 12.9 B
## 9 11.7 B
## 10 13.0 BSiempre y cuando no haya vínculos (es decir, personas con exactamente la misma puntuación de awesomeness), entonces la prueba que queremos hacer es sorprendentemente simple. Todo lo que tenemos que hacer es construir una tabla que compare cada observación del grupo A con cada observación del grupo B. Siempre que el dato del grupo A sea mayor, colocamos una marca de verificación en la tabla:

Luego contamos el número de marcas de verificación. Este es nuestro estadístico de prueba, W. 200 La distribución real del muestreo para W es algo complicada, y me saltaré los detalles. Para nuestros propósitos, basta con señalar que la interpretación de W es cualitativamente la misma que la interpretación de t o z, es decir, si queremos una prueba bilateral, entonces rechazamos la hipótesis nula cuando W es muy grande o muy pequeña; pero si tenemos una hipótesis direccional (es decir, unilateral), entonces solo usamos uno o el otro.
La estructura de la función wilcox.test () ya debería resultarte muy familiar. Cuando tienes tus datos organizados en términos de una variable de resultado y una variable de agrupación, entonces usas la fórmula y los argumentos de datos, por lo que tu comando se ve así:
wilcox.test( formula = scores ~ group, data = awesome)##
## Wilcoxon rank sum test
##
## data: scores by group
## W = 3, p-value = 0.05556
## alternative hypothesis: true location shift is not equal to 0Al igual que vimos con la función t.test (), hay un argumento alternativo que puedes usar para alternar entre pruebas de dos caras y pruebas unilaterales, además de algunos otros argumentos de los que no necesitamos preocuparnos demasiado a nivel introductorio. Del mismo modo, la función wilcox.test () le permite utilizar los argumentos x e y cuando tenga sus datos almacenados por separado para cada grupo. Por ejemplo, supongamos que usamos los datos del archivo Awesome2.rData:
load( "./rbook-master/data/awesome2.Rdata" )
score.A## [1] 6.4 10.7 11.9 7.3 10.0
score.B## [1] 14.5 10.4 12.9 11.7 13.0Cuando tus datos están organizados así, entonces usarías un comando como este:
wilcox.test( x = score.A, y = score.B )##
## Wilcoxon rank sum test
##
## data: score.A and score.B
## W = 3, p-value = 0.05556
## alternative hypothesis: true location shift is not equal to 0La salida que produce R es prácticamente la misma que la última vez.
muestra de prueba de Wilcoxon
¿Qué pasa con la prueba de Wilcoxon de una muestra (o equivalentemente, la prueba de Wilcoxon de muestras pareadas)? Supongamos que me interesa saber si tomar una clase de estadística tiene algún efecto en la felicidad de los estudiantes. Aquí están mis datos:
load( "./rbook-master/data/happy.Rdata" )
print( happiness )## before after change
## 1 30 6 -24
## 2 43 29 -14
## 3 21 11 -10
## 4 24 31 7
## 5 23 17 -6
## 6 40 2 -38
## 7 29 31 2
## 8 56 21 -35
## 9 38 8 -30
## 10 16 21 5Lo que he medido aquí es la felicidad de cada alumno antes de tomar la clase y después de tomar la clase; el puntaje de cambio es la diferencia entre los dos. Al igual que vimos con la prueba t, no hay diferencia fundamental entre hacer una prueba de muestras emparejadas usando antes y después, versus hacer una prueba de una muestra usando los puntajes de cambio. Como antes, la forma más sencilla de pensar sobre la prueba es construir una tabulación. La forma de hacerlo en esta ocasión es tomar esas puntuaciones de cambio que sean valoradas positivamente, y tabularlas contra toda la muestra completa. Con lo que terminas es una mesa que se ve así:
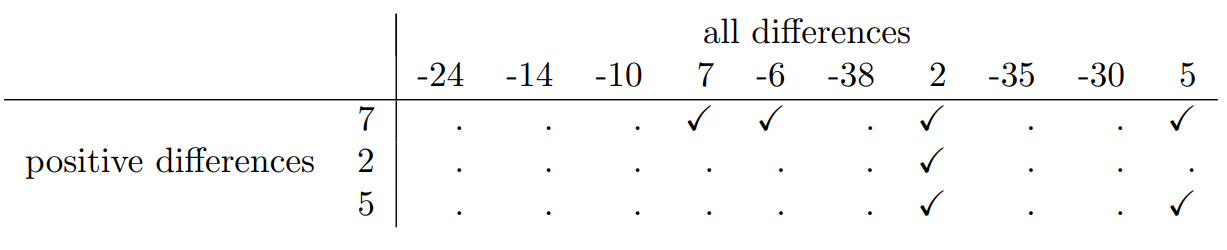
Contando las marcas esta vez, obtenemos un estadístico de prueba de V=7. Como antes, si nuestra prueba es bilateral, entonces rechazamos la hipótesis nula cuando V es muy grande o muy pequeña. En cuanto a ejecutarlo en R va, es más o menos lo que esperarías. Para la versión de una muestra, el comando que usarías es
wilcox.test( x = happiness$change,
mu = 0
)##
## Wilcoxon signed rank test
##
## data: happiness$change
## V = 7, p-value = 0.03711
## alternative hypothesis: true location is not equal to 0Como esto muestra, tenemos un efecto significativo. Evidentemente, tomar una clase de estadística sí tiene un efecto en tu felicidad. Cambiar a una versión de muestras pareadas de la prueba no nos dará respuestas diferentes, por supuesto; pero aquí está el comando para hacerlo:
wilcox.test( x = happiness$after,
y = happiness$before,
paired = TRUE
)##
## Wilcoxon signed rank test
##
## data: happiness$after and happiness$before
## V = 7, p-value = 0.03711
## alternative hypothesis: true location shift is not equal to 0 

