14.3: Cómo funciona ANOVA
- Page ID
- 151296
Para responder a la pregunta planteada por nuestros datos de ensayos clínicos, vamos a ejecutar un ANOVA unidireccional. Como de costumbre, voy a comenzar mostrándote cómo hacerlo de la manera difícil, construyendo la herramienta estadística desde cero y mostrándote cómo podrías hacerlo en R si no tuvieras acceso a ninguna de las geniales funciones de ANOVA incorporadas. Y, como siempre, espero que lo lean con atención, traten de hacerlo a lo largo una o dos veces para asegurarse de que realmente entienden cómo funciona el ANOVA, y luego —una vez que haya comprendido el concepto— nunca más lo vuelvas a hacer de esta manera.
El diseño experimental que describí en la sección anterior sugiere fuertemente que estamos interesados en comparar el cambio de humor promedio para los tres medicamentos diferentes. En ese sentido, estamos hablando de un análisis similar a la prueba t (Capítulo 13, pero involucrando a más de dos grupos. Si dejamos que μ P denote la media poblacional para el cambio de humor inducido por el placebo, y dejamos que μ A y μ J denoten las medias correspondientes para nuestros dos fármacos, Anxifree y Joyzepam, entonces la hipótesis nula (algo pesimista) que queremos probar es que las tres poblaciones los medios son idénticos: es decir, ninguno de los dos fármacos es más efectivo que un placebo. Matemáticamente, escribimos esta hipótesis nula así:
H 0: es cierto que μ P =μ A =μ J
Como consecuencia, nuestra hipótesis alternativa es que al menos uno de los tres tratamientos diferentes es diferente de los demás. Es un poco más complicado escribir esto matemáticamente, porque (como discutiremos) hay bastantes formas diferentes en las que la hipótesis nula puede ser falsa. Así que por ahora solo escribiremos la hipótesis alternativa así:
H 1: es *no* cierto que μ P =μ A =μ J
Esta hipótesis nula es mucho más difícil de probar que cualquiera de las que hemos visto anteriormente. ¿Cómo lo haremos? Una suposición sensata sería “hacer un ANOVA”, ya que ese es el título del capítulo, pero no está particularmente claro por qué un “análisis de varianzas” nos ayudará a aprender algo útil sobre los medios. De hecho, esta es una de las mayores dificultades conceptuales que tienen las personas al encontrarse por primera vez con ANOVA. Para ver cómo funciona esto, me parece de lo más útil comenzar hablando de varianzas. De hecho, lo que voy a hacer es empezar por jugar algunos juegos matemáticos con la fórmula que describe la varianza. Es decir, comenzaremos jugando con varianzas, y resultará que esto nos da una herramienta útil para investigar los medios.
fórmulas para la varianza de Y
En primer lugar, comencemos introduciendo alguna notación. Usaremos G para referirnos al número total de grupos. Para nuestro conjunto de datos, hay tres fármacos, por lo que hay grupos G=3. A continuación, usaremos N para referirnos al tamaño total de la muestra: hay un total de N=18 personas en nuestro conjunto de datos. De igual manera, usemos N k para denotar el número de personas en el k-ésimo grupo. En nuestro ensayo clínico falso, el tamaño de la muestra es N k =6 para los tres grupos. 201 Finalmente, usaremos Y para denotar la variable de resultado: en nuestro caso, Y se refiere al cambio de humor. Específicamente, usaremos Y ik para referirnos al cambio de humor experimentado por el i-ésimo miembro del k-ésimo grupo. Del mismo modo, solemos ser el cambio de humor promedio, tomado\(\ \bar{Y}\) a través de las 18 personas en el experimento, y\(\ \bar{Y_k}\) para referirnos al cambio de humor promedio experimentado por las 6 personas en el grupo k.
Excelente. Ahora que tenemos nuestra notación resuelta, podemos empezar a escribir fórmulas. Para empezar, recordemos la fórmula para la varianza que usamos en la Sección 5.2, muy atrás en esos días más amables cuando solo estábamos haciendo estadísticas descriptivas. La varianza muestral de Y se define de la siguiente manera:
\(\operatorname{Var}(Y)=\dfrac{1}{N} \sum_{k=1}^{G} \sum_{i=1}^{N_{k}}\left(Y_{i k}-\bar{Y}\right)^{2}\)
Esta fórmula se ve prácticamente idéntica a la fórmula para la varianza en la Sección 5.2. La única diferencia es que en esta ocasión tengo dos sumas aquí: estoy sumando sobre grupos (es decir, valores para k) y sobre las personas dentro de los grupos (es decir, valores para i). Esto es puramente un detalle cosmético: si en su lugar hubiera usado la notación Y p para referirme al valor de la variable de resultado para la persona p en la muestra, entonces solo tendría una sola suma. La única razón por la que tenemos una doble suma aquí es que he clasificado a las personas en grupos, y luego asigné números a personas dentro de grupos.
Un ejemplo concreto podría ser útil aquí. Consideremos esta tabla, en la que tenemos un total de N=5 personas ordenadas en grupos G=2. Arbitrariamente, digamos que la gente “cool” es el grupo 1, y la gente “poco cool” es el grupo 2, y resulta que tenemos tres personas geniales (N 1 =3) y dos personas poco cool (N 2 =2).
| nombre | persona (p) | grupo | grupo num (k) | índice en el grupo (i) | gruñido (Y ik o Y p) |
|---|---|---|---|---|---|
| Ann | 1 | cool | 1 | 1 | 20 |
| Ben | 2 | cool | 1 | 2 | 55 |
| Cat | 3 | cool | 1 | 3 | 21 |
| Dan | 4 | uncool | 2 | 1 | 91 |
| Huevo | 5 | uncool | 2 | 2 | 22 |
Observe que aquí he construido dos esquemas de etiquetado diferentes. Tenemos una variable “persona” p, por lo que sería perfectamente sensato referirse a Y p como la maldad de la p-ésima persona en la muestra. Por ejemplo, la tabla muestra que Dan es el cuatro así que diríamos p=4. Entonces, al hablar de la maldad Y de esta persona “Dan”, quienquiera que sea, podríamos referirnos a su maldad diciendo que Y p =91, para persona p=4 es decir. No obstante, esa no es la única forma en que podríamos referirnos a Dan. Como alternativa podríamos señalar que Dan pertenece al grupo “uncool” (k=2), y de hecho es la primera persona listada en el grupo uncool (i=1). Entonces es igualmente válido referirse al mal humor de Dan diciendo que Y ik =91, donde k=2 e i=1. En otras palabras, cada persona p corresponde a una combinación ik única, y así la fórmula que di anteriormente es en realidad idéntica a nuestra fórmula original para la varianza, que sería
\(\operatorname{Var}(Y)=\dfrac{1}{N} \sum_{p=1}^{N}\left(Y_{p}-\bar{Y}\right)^{2}\)
En ambas fórmulas, lo único que estamos haciendo es sumar todas las observaciones de la muestra. La mayoría de las veces simplemente usaríamos la notación Y p más simple: la ecuación que usa Y p es claramente la más simple de las dos. Sin embargo, al hacer un ANOVA es importante hacer un seguimiento de qué participantes pertenecen a qué grupos, y necesitamos usar la notación Y ik para hacer esto.
De varianzas a sumas de cuadrados
Bien, ahora que tenemos una buena comprensión de cómo se calcula la varianza, definamos algo llamado la suma total de cuadrados, que se denota SS tot. Esto es muy sencillo: en lugar de promediar las desviaciones cuadradas, que es lo que hacemos al calcular la varianza, simplemente las sumamos. Entonces la fórmula para la suma total de cuadrados es casi idéntica a la fórmula para la varianza:
\(\mathrm{SS}_{t o t}=\sum_{k=1}^{G} \sum_{i=1}^{N_{k}}\left(Y_{i k}-\bar{Y}\right)^{2}\)
Cuando hablamos de analizar varianzas en el contexto del ANOVA, lo que realmente estamos haciendo es trabajar con las sumas totales de cuadrados en lugar de la varianza real. Una cosa muy agradable de la suma total de cuadrados es que podemos dividirla en dos tipos diferentes de variación. En primer lugar, podemos hablar de la suma de cuadrados dentro del grupo, en la que miramos para ver cuán diferente es cada persona individual de su propio grupo significa:
\(\mathrm{SS}_{w}=\sum_{k=1}^{G} \sum_{i=1}^{N_{k}}\left(Y_{i k}-\bar{Y}_{k}\right)^{2}\)
donde\(\ \bar{Y_k}\) es una media grupal. En nuestro ejemplo,\(\ \bar{Y_k}\) sería el cambio de humor promedio experimentado por aquellas personas a las que se les dio el k-ésimo medicamento. Entonces, en lugar de comparar individuos con el promedio de todas las personas en el experimento, solo los estamos comparando con aquellas personas del mismo grupo. Como consecuencia, se esperaría que el valor de SS w sea menor que la suma total de cuadrados, porque está ignorando completamente cualquier diferencia de grupo, es decir, el hecho de que las drogas (si funcionan) tendrán diferentes efectos en el estado de ánimo de las personas.
A continuación, podemos definir una tercera noción de variación que captura solo las diferencias entre grupos. Esto lo hacemos observando las diferencias entre las medias grupales\(\ \bar{Y_k}\) y la gran media\(\ \bar{Y}\). Para cuantificar la extensión de esta variación, lo que hacemos es calcular la suma de cuadrados entre grupos:
\(\begin{aligned} \mathrm{SS}_{b} &=\sum_{k=1}^{G} \sum_{i=1}^{N_{k}}\left(\bar{Y}_{k}-\bar{Y}\right)^{2} \\ &=\sum_{k=1}^{G} N_{k}\left(\bar{Y}_{k}-\bar{Y}\right)^{2} \end{aligned}\)
No es demasiado difícil demostrar que la variación total entre las personas en el experimento SS tot es en realidad la suma de las diferencias entre los grupos SS b y la variación dentro de los grupos SS w. Es decir:
SS w +SS b =SS tot
¡Hurra!
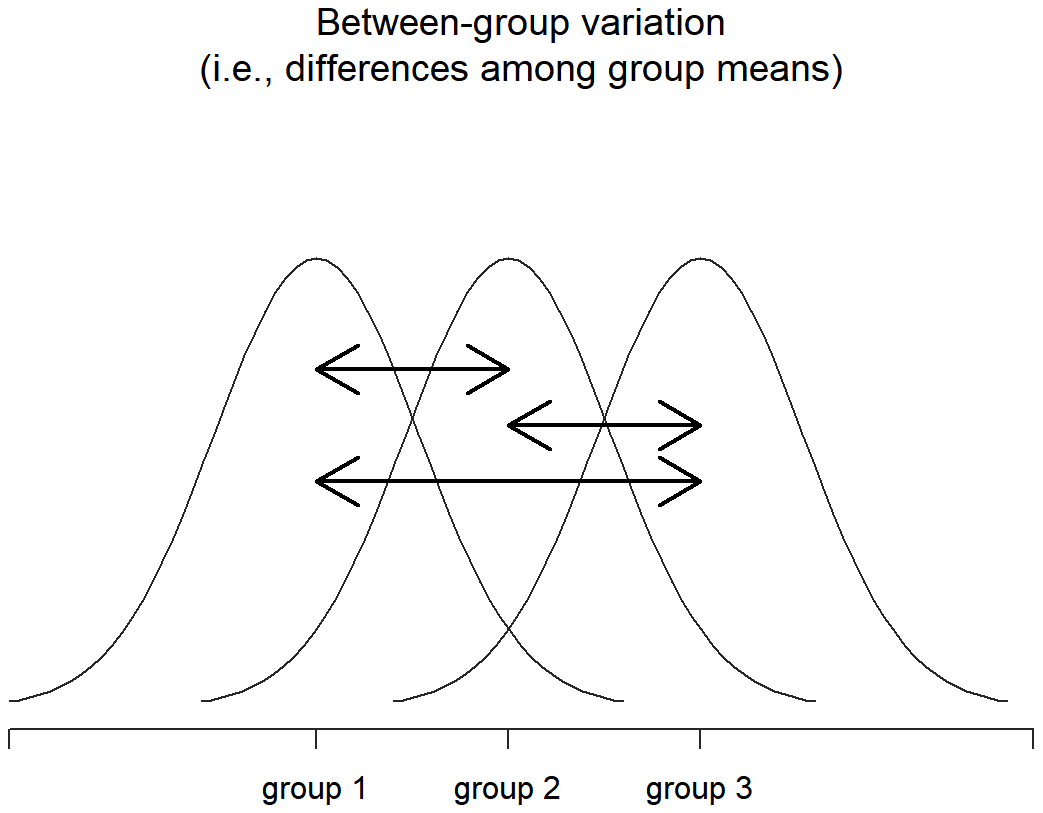
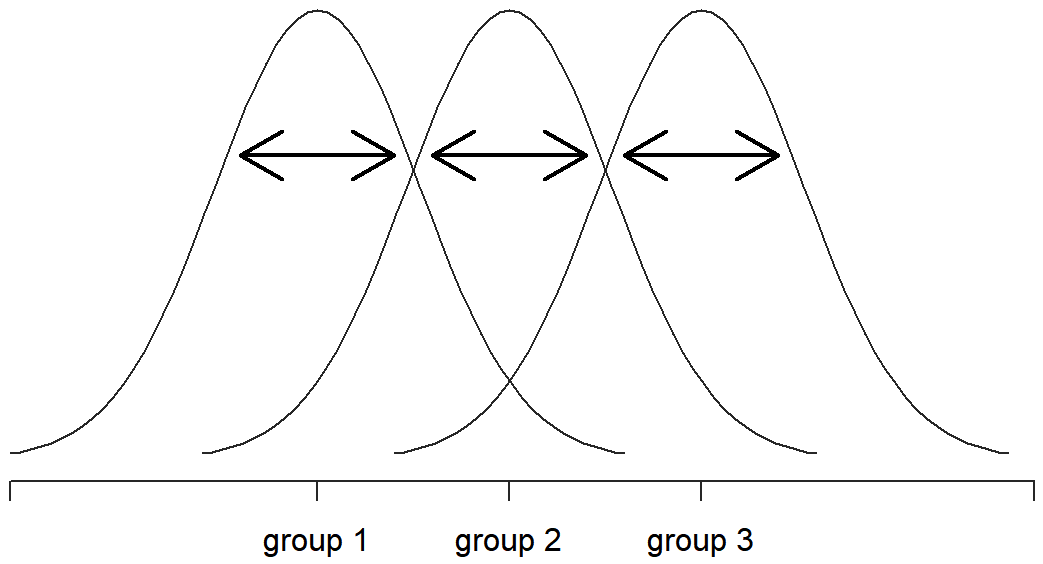
Bien, entonces, ¿qué hemos averiguado? Hemos descubierto que la variabilidad total asociada a la variable de resultado (SS tot) se puede dividir matemáticamente en la suma de “la variación por las diferencias en las medias de la muestra para los diferentes grupos” (SS b) más “todo el resto de la variación” (SS w). ¿Cómo me ayuda eso a averiguar si los grupos tienen diferentes medios de población? Um. Espera. Espera un segundo... ahora que lo pienso, esto es exactamente lo que estábamos buscando. Si la hipótesis nula es cierta, entonces esperarías que todos los medios de muestra sean bastante similares entre sí, ¿verdad? Y eso implicaría que esperarías que SS b sea realmente pequeño, o al menos esperarías que fuera mucho más pequeño que la “la variación asociada con todo lo demás”, SS w. Hm. Detecto una prueba de hipótesis viniendo en...
De sumas de cuadrados a la prueba F
Como vimos en la última sección, la idea cualitativa detrás de ANOVA es comparar las dos sumas de los valores cuadrados SS b y SS w entre sí: si la variación entre grupos es SS b es grande en relación con la variación dentro del grupo SS w entonces tenemos razones para sospechar que los medios poblacionales para los diferentes grupos no son idénticos entre sí. Para convertir esto en una prueba de hipótesis viable, se necesita un poco de “juguetear”. Lo que haré es primero mostrarte lo que hacemos para calcular nuestra estadística de prueba —que se llama relación F — y luego tratar de darte una idea de por qué lo hacemos de esta manera.
Para convertir nuestros valores SS en una relación F, lo primero que necesitamos calcular son los grados de libertad asociados a los valores SSb y SS w. Como es habitual, los grados de libertad corresponden al número de “puntos de datos” únicos que contribuyen a un cálculo particular, menos el número de “restricciones” que necesitan satisfacer. Para la variabilidad dentro de grupos, lo que estamos calculando es la variación de las observaciones individuales (N puntos de datos) alrededor de las medias del grupo (restricciones G). En contraste, para la variabilidad entre grupos, nos interesa la variación de las medias grupales (puntos de datos G) alrededor de la gran media (1 restricción). Por lo tanto, los grados de libertad aquí son:
df b =G−1
df w =N−G
Bien, eso parece bastante sencillo. Lo que hacemos a continuación es convertir nuestro valor de cuadrados sumados en un valor de “cuadrados medios”, lo que hacemos dividiendo por los grados de libertad:
\(\ MS_b = {SS_b \over df_b} \)
\(\ MS_w = {SS_w \over df_w} \)
Finalmente, calculamos la relación F dividiendo la EM entre grupos por la EM dentro de los grupos:
\(\ F={MS_b \over MS_w} \)
A un nivel muy general, la intuición detrás del estadístico F es sencilla: valores mayores de F significa que la variación entre grupos es grande, relativa a la variación dentro de los grupos. Como consecuencia, cuanto mayor sea el valor de F, más evidencia tenemos contra la hipótesis nula. Pero, ¿qué tan grande tiene que ser F para poder rechazar realmente H 0? Para entender esto, se necesita una comprensión un poco más profunda de qué es el ANOVA y cuáles son realmente los valores de cuadrados medios.
En la siguiente sección se discute eso con un poco de detalle, pero para los lectores que no están interesados en los detalles de lo que realmente está midiendo la prueba, voy a ir al grano. Para completar nuestra prueba de hipótesis, necesitamos conocer la distribución de muestreo para F si la hipótesis nula es verdadera. No es sorprendente que la distribución de muestreo para el estadístico F bajo la hipótesis nula sea una distribución F. Si recuerdas de nuevo a nuestra discusión de la distribución F en el Capítulo @ref (probabilidad, la distribución F tiene dos parámetros, correspondientes a los dos grados de libertad involucrados: el primero df1 es el entre grupos grados de libertad dfb, y el segundo df2 es el dentro de grupos grados de libertad df w.
En la Tabla 14.1 se muestra un resumen de todas las cantidades clave involucradas en un ANOVA unidireccional, incluyendo las fórmulas que muestran cómo se calculan.
Cuadro 14.1: Todas las cantidades clave involucradas en un ANOVA, organizadas en una tabla ANOVA “estándar”. Se muestran las fórmulas para todas las cantidades (excepto el valor p, que tiene una fórmula muy fea y sería pesadamente difícil de calcular sin computadora).
| df | suma de cuadrados | cuadrados medios | Estadística F | valor p | |
|---|---|---|---|---|---|
| entre grupos | df b =G−1 | \(\mathrm{SS}_{b}=\sum_{k=1}^{G} N_{k}\left(\bar{Y}_{k}-\bar{Y}\right)^{2}\) | \(\mathrm{MS}_{b}=\dfrac{\mathrm{SS}_{b}}{\mathrm{df}_{b}}\) | \(F=\dfrac{\mathrm{MS}_{b}}{\mathrm{MS}_{w}}\) | [complicado] |
| dentro de grupos | df w =N−G | \(SS_w=\sum_{k=1}^{G} \sum_{i=1}^{N_{k}}\left(Y_{i k}-\bar{Y}_{k}\right)^{2}\) | \(\mathrm{MS}_{w}=\dfrac{\mathrm{SS}_{w}}{\mathrm{df}_{w}}\) | - | - |
modelo para los datos y el significado de F (avanzado)
A nivel fundamental, ANOVA es una competencia entre dos modelos estadísticos diferentes, H 0 y H 1. Cuando describí las hipótesis nulas y alternativas al inicio de la sección, fui un poco impreciso sobre cuáles son en realidad estos modelos. Voy a remediar eso ahora, aunque probablemente no te guste por hacerlo. Si recuerda, nuestra hipótesis nula fue que todas las medias grupales son idénticas entre sí. Si es así, entonces una manera natural de pensar sobre la variable de resultado Y ik es describir las puntuaciones individuales en términos de una sola media poblacional μ, más la desviación de esa media poblacional. Esta desviación suele ser denotada como ik y tradicionalmente se llama el error o residual asociado a esa observación. Sin embargo, ten cuidado: al igual que vimos con la palabra “significativo”, la palabra “error” tiene un significado técnico en estadística que no es exactamente lo mismo que su definición cotidiana en inglés. En el lenguaje cotidiano, el “error” implica un error de algún tipo; en la estadística, no lo hace (o al menos, no necesariamente). Con eso en mente, la palabra “residual” es un término mejor que la palabra “error”. En estadística, ambas palabras significan “variabilidad sobrante”: es decir, “cosas” que el modelo no puede explicar. En cualquier caso, así es como se ve la hipótesis nula cuando la escribimos como modelo estadístico:
Y ik =μ+ik
donde hacemos la suposición (discutida más adelante) de que los valores residuales ik se distribuyen normalmente, con una media 0 y una desviación estándar σ que es la misma para todos los grupos. Para usar la notación que introdujimos en el Capítulo 9 escribiríamos esta suposición así:
ik ~ Normal (0, σ 2)
¿Y la hipótesis alternativa, H 1? La única diferencia entre la hipótesis nula y la hipótesis alternativa es que permitimos que cada grupo tenga una media poblacional diferente. Entonces, si dejamos que μk denote la media poblacional para el k-ésimo grupo en nuestro experimento, entonces el modelo estadístico correspondiente a H 1 es:
Y ik = μ k +ik
donde, una vez más, suponemos que los términos de error se distribuyen normalmente con media 0 y desviación estándar σ. Es decir, la hipótesis alternativa también asume que
~ Normal (0, σ 2)
Bien, ahora que hemos descrito los modelos estadísticos que sustentan H 0 y H 1 con más detalle, ahora es bastante sencillo decir qué miden los valores cuadrados medios, y qué significa esto para la interpretación de F. No te aburriré con la prueba de esto, pero resulta que el cuadrado medio dentro de los grupos, MS w, puede ser visto como un estimador (en el sentido técnico: Capítulo 10 de la varianza de error σ 2. La media cuadrática media MS b es también un estimador; pero lo que estima es la varianza del error más una cantidad que depende de las verdaderas diferencias entre las medias del grupo. Si llamamos a esta cantidad Q, entonces podemos ver que la estadística F es básicamente 202
\(F=\dfrac{\hat{Q}+\hat{\sigma}^{2}}{\hat{\sigma}^{2}}\)
donde el valor verdadero Q=0 si la hipótesis nula es verdadera, y Q>0 si la hipótesis alternativa es verdadera (por ejemplo, cap. 10 Hays 1994). Por lo tanto, como mínimo, el valor F debe ser mayor que 1 para tener alguna posibilidad de rechazar la hipótesis nula. Tenga en cuenta que esto no significa que sea imposible obtener un valor F menor que 1. Lo que significa es que, si la hipótesis nula es verdadera la distribución muestral de la relación F tiene una media de 1, 203 y así necesitamos ver valores F mayores que 1 para poder rechazar de manera segura el nulo.
Para ser un poco más precisos acerca de la distribución muestral, observe que si la hipótesis nula es verdadera, tanto MS b como MS w son estimadores de la varianza de los residuales, ik. Si esos residuos se distribuyen normalmente, entonces podrías sospechar que la estimación de la varianza de ik es chi-cuadrada distribuida... porque (como se discute en la Sección 9.6 eso es lo que es una distribución chi-cuadrada: es lo que obtienes cuando cuadras un montón de normalmente- distribuyó las cosas y sumarlas. Y como la distribución F es (de nuevo, por definición) lo que obtienes cuando tomas la relación entre dos cosas que son X 2 distribuidas... tenemos nuestra distribución de muestreo. Obviamente, estoy pasando por alto muchas cosas cuando digo esto, pero en términos generales, de aquí realmente es de donde proviene nuestra distribución de muestreo.
ejemplo trabajado
La discusión anterior fue bastante abstracta, y un poco en el aspecto técnico, por lo que creo que en este punto podría ser útil ver un ejemplo trabajado. Para eso, volvamos a los datos de los ensayos clínicos que introduje al inicio del capítulo. Las estadísticas descriptivas que calculamos al inicio nos indican las medias de nuestro grupo: una ganancia promedio del estado de ánimo de 0.45 para el placebo, 0.72 para Anxifree y 1.48 para Joyzepam. Con eso en mente, festejemos como si fuera 1899 204 y empecemos a hacer algunos cálculos a lápiz y papel. Sólo voy a hacer esto para las primeras 5 observaciones, porque no es sangriento 1899 y soy muy vago. Empecemos calculando SS w, las sumas de cuadrados dentro del grupo. Primero, hagamos una linda mesa para ayudarnos con nuestros cálculos...
| grupo (k) | resultado (Y ik) |
|---|---|
| placebo | 0.5 |
| placebo | 0.3 |
| placebo | 0.1 |
| ansioso | 0.6 |
| ansioso | 0.4 |
En esta etapa, lo único que he incluido en la tabla son los datos brutos en sí: es decir, la variable de agrupación (es decir, droga) y la variable de resultado (es decir, estado de ánimo.ganancia) para cada persona. Tenga en cuenta que la variable de resultado aquí corresponde al valor Y ik en nuestra ecuación anteriormente. El siguiente paso en el cálculo es anotar, para cada persona en el estudio, la media grupal correspondiente; es decir,\(\ \bar{Y_k}\). Esto es un poco repetitivo, pero no particularmente difícil ya que ya calculamos esas medias grupales al hacer nuestras estadísticas descriptivas:
| grupo (k) | resultado (Y ik) | media del grupo (\(\ \bar{Y_k}\) |
|---|---|---|
| placebo | 0.5 | 0.45 |
| placebo | 0.3 | 0.45 |
| placebo | 0.1 | 0.45 |
| ansioso | 0.6 | 0.72 |
| ansioso | 0.4 | 0.72 |
Ahora que los hemos anotado, necesitamos calcular —de nuevo para cada persona— la desviación de la media del grupo correspondiente. Es decir, queremos restar Y ik −\(\ \bar{Y_k}\). Después de que lo hayamos hecho, tenemos que cuadrar todo. Cuando hacemos eso, esto es lo que obtenemos:
| grupo (k) | resultado (Y ik) | media del grupo (\(\ \bar{Y_k}\)) | dev. de la media del grupo (Y ik −\(\ \bar{Y_k}\)) | desviación cuadrada ((Y ik −\(\ \bar{Y_k}\)) 2) |
|---|---|---|---|---|
| placebo | 0.5 | 0.45 | 0.05 | 0.0025 |
| placebo | 0.3 | 0.45 | -0.15 | 0.0225 |
| placebo | 0.1 | 0.45 | -0.35 | 0.1225 |
| ansioso | 0.6 | 0.72 | -0.12 | 0.0136 |
| ansioso | 0.4 | 0.72 | -0.32 | 0.1003 |
El último paso es igualmente sencillo. Para calcular la suma de cuadrados dentro del grupo, solo sumamos las desviaciones cuadradas en todas las observaciones:
\(\begin{aligned} \mathrm{SS}_{w} &=0.0025+0.0225+0.1225+0.0136+0.1003 \\ &=0.2614 \end{aligned}\)
Por supuesto, si realmente quisiéramos obtener la respuesta correcta, tendríamos que hacer esto para las 18 observaciones del conjunto de datos, no solo las primeras cinco. Podríamos continuar con los cálculos a lápiz y papel si quisiéramos, pero es bastante tedioso. Alternativamente, no es demasiado difícil conseguir que R lo haga. He aquí cómo:
outcome <- clin.trial$mood.gain
group <- clin.trial$drug
gp.means <- tapply(outcome,group,mean)
gp.means <- gp.means[group]
dev.from.gp.means <- outcome - gp.means
squared.devs <- dev.from.gp.means ^2Puede que no sea obvio a partir de la inspección lo que están haciendo estos comandos: como regla general, el cerebro humano parece simplemente apagarse cuando se enfrenta a un gran bloque de programación. No obstante, te sugiero fuertemente que —si eres como yo y tiendes a encontrar que la mera vista de este código te hace querer mirar hacia otro lado y ver si queda alguna cerveza en la nevera o un juego de fútbol en la tele— te tomes un momento y miras de cerca estos comandos uno a la vez. Cada uno de estos comandos es algo que has visto antes en algún otro lugar del libro. No hay nada novedoso en ellos (aunque tendré que admitir que la función tapply () tarda un tiempo en manejarse), así que si no estás muy seguro de cómo funcionan estos comandos, este podría ser un buen momento para intentar jugar con ellos tú mismo, para tratar de tener una idea de lo que está sucediendo. Por otro lado, si esto parece tener sentido, entonces no te sorprenderá tanto lo que sucede cuando envuelvo estas variables en un marco de datos, y lo imprimo...
Y <- data.frame( group, outcome, gp.means,
dev.from.gp.means, squared.devs )
print(Y, digits = 2)## group outcome gp.means dev.from.gp.means squared.devs
## 1 placebo 0.5 0.45 0.050 0.0025
## 2 placebo 0.3 0.45 -0.150 0.0225
## 3 placebo 0.1 0.45 -0.350 0.1225
## 4 anxifree 0.6 0.72 -0.117 0.0136
## 5 anxifree 0.4 0.72 -0.317 0.1003
## 6 anxifree 0.2 0.72 -0.517 0.2669
## 7 joyzepam 1.4 1.48 -0.083 0.0069
## 8 joyzepam 1.7 1.48 0.217 0.0469
## 9 joyzepam 1.3 1.48 -0.183 0.0336
## 10 placebo 0.6 0.45 0.150 0.0225
## 11 placebo 0.9 0.45 0.450 0.2025
## 12 placebo 0.3 0.45 -0.150 0.0225
## 13 anxifree 1.1 0.72 0.383 0.1469
## 14 anxifree 0.8 0.72 0.083 0.0069
## 15 anxifree 1.2 0.72 0.483 0.2336
## 16 joyzepam 1.8 1.48 0.317 0.1003
## 17 joyzepam 1.3 1.48 -0.183 0.0336
## 18 joyzepam 1.4 1.48 -0.083 0.0069Si comparas esta salida con el contenido de la tabla que he estado construyendo a mano, puedes ver que R ha hecho exactamente los mismos cálculos que yo estaba haciendo, y mucho más rápido también. Entonces, si queremos terminar los cálculos de la suma de cuadrados dentro del grupo en R, solo pedimos la suma () de la variable squared.devs:
SSw <- sum( squared.devs )
print( SSw )
## [1] 1.391667Obviamente, esto no es lo mismo que calculé, porque R utilizó las 18 observaciones. Pero si hubiera escrito sum (squared.devs [1:5]) en su lugar, habría dado la misma respuesta que obtuve antes.
Bien. Ahora que hemos calculado la variación dentro de grupos, SS w, es el momento de dirigir nuestra atención a la suma de cuadrados entre grupos, SS b. Los cálculos para este caso son muy similares. La principal diferencia es que, en lugar de calcular las diferencias entre una observación Y ik y una media grupal\(\ \bar{Y_k}\) para todas las observaciones, calculamos las diferencias entre las medias grupales\(\ \bar{Y_k}\) y la media general\(\ \bar{Y}\) (en este caso 0.88) para todos los grupos...
| grupo (k) | media del grupo (\(\ \bar{Y_k}\)) | gran media (\(\ \bar{Y}\)) | desviación (\(\ \bar{Y_k} - \bar{Y}\)) | desviaciones cuadradas ((\(\ \bar{Y_k} - \bar{Y}\)) 2) |
|---|---|---|---|---|
| placebo | 0.45 | 0.88 | -0.43 | 0.18 |
| ansioso | 0.72 | 0.88 | -0.16 | 0.03 |
| joyzepam | 1.48 | 0.88 | 0.60 | 0.36 |
Sin embargo, para los cálculos entre grupos necesitamos multiplicar cada una de estas desviaciones cuadradas por N k, el número de observaciones en el grupo. Hacemos esto porque cada observación en el grupo (todas N k de ellas) está asociada con una diferencia entre grupos. Entonces, si hay seis personas en el grupo placebo, y la media del grupo placebo difiere de la gran media en 0.19, entonces la variación total entre grupos asociada a estas seis personas es 6×0.16=1.14. Entonces tenemos que extender nuestra mesita de cálculos...
| grupo (k) | desviaciones cuadradas ((\(\ \bar{Y_k} - \bar{Y}\)) 2) | tamaño de la muestra (N k) | desarrollo cuadrado ponderado (N k (\(\ \bar{Y_k} - \bar{Y}\)) 2) |
|---|---|---|---|
| placebo | 0.18 | 6 | 1.11 |
| ansioso | 0.03 | 6 | 0.16 |
| joyzepam | 0.36 | 6 | 2.18 |
Y así ahora nuestra suma de cuadrados entre grupos se obtiene sumando estas “desviaciones ponderadas al cuadrado” sobre los tres grupos del estudio:
\(\begin{aligned} \mathrm{SS}_{b} &=1.11+0.16+2.18 \\ &=3.45 \end{aligned}\)
Como puede ver, los cálculos entre grupos son mucho más cortos, por lo que probablemente no suele querer molestarse en usar R como su calculadora. Sin embargo, si decidiste hacerlo, aquí tienes una forma de hacerlo:
gp.means <- tapply(outcome,group,mean)
grand.mean <- mean(outcome)
dev.from.grand.mean <- gp.means - grand.mean
squared.devs <- dev.from.grand.mean ^2
gp.sizes <- tapply(outcome,group,length)
wt.squared.devs <- gp.sizes * squared.devsNuevamente, en realidad no voy a tratar de explicar este código línea por línea, pero —igual que la última vez— no hay nada ahí dentro que no hayamos visto en varios lugares del libro, así que lo dejaré como un ejercicio para que te asegures de que lo entiendes. Una vez más, podemos volcar todas nuestras variables en un marco de datos para que podamos imprimirlo como una bonita tabla:
Y <- data.frame( gp.means, grand.mean, dev.from.grand.mean,
squared.devs, gp.sizes, wt.squared.devs )
print(Y, digits = 2) ## gp.means grand.mean dev.from.grand.mean squared.devs gp.sizes
## placebo 0.45 0.88 -0.43 0.188 6
## anxifree 0.72 0.88 -0.17 0.028 6
## joyzepam 1.48 0.88 0.60 0.360 6
## wt.squared.devs
## placebo 1.13
## anxifree 0.17
## joyzepam 2.16Claramente, estos son básicamente los mismos números que obtuvimos antes. Hay algunas diferencias diminutas, pero eso es solo porque las versiones calculadas a mano tienen algunos pequeños errores causados por el hecho de que redondeé todos mis números a 2 decimales en cada paso de los cálculos, mientras que R solo lo hace al final (obviamente, la versión R s es más precisa). De todos modos, aquí está el comando R que muestra el paso final:
SSb <- sum( wt.squared.devs )
print( SSb ) ## [1] 3.453333que es (ignorando las ligeras diferencias por error de redondeo) la misma respuesta que obtuve al hacer las cosas a mano.
Ahora que hemos calculado nuestras sumas de valores cuadrados, SS b y SS w, el resto del ANOVA es bastante indoloro. El siguiente paso es calcular los grados de libertad. Dado que tenemos G=3 grupos y N=18 observaciones en total, nuestros grados de libertad se pueden calcular por simple resta:
df b =G−1=2
df w =N−G=15
A continuación, ya que ahora hemos calculado los valores para las sumas de cuadrados y los grados de libertad, tanto para la variabilidad dentro de grupos como para la variabilidad entre grupos, podemos obtener los valores cuadrados medios dividiendo uno por otro:
\(\mathrm{MS}_{b}=\dfrac{\mathrm{SS}_{b}}{\mathrm{df}_{b}}=\dfrac{3.45}{2}=1.73\)
\(\mathrm{MS}_{w}=\dfrac{\mathrm{SS}_{w}}{\mathrm{df}_{w}}=\dfrac{1.39}{15}=0.09\)
Ya casi terminamos. Los valores cuadrados medios se pueden utilizar para calcular el valor F, que es el estadístico de prueba que nos interesa. Esto lo hacemos dividiendo el valor de MS entre grupos por el valor de MS dentro de los grupos y dentro de los grupos.
\(\ F={MS_b \over MS_w} = {1.73 \over 0.09}=18.6\)
¡Woohooo! Esto es terriblemente emocionante, ¿sí? Ahora que tenemos nuestro estadístico de prueba, el último paso es averiguar si la prueba en sí nos da un resultado significativo. Como se discutió en el Capítulo @ref (hipotesisting, lo que realmente debemos hacer es elegir un nivel α (es decir, tasa de error aceptable de Tipo I) antes de tiempo, construir nuestra región de rechazo, etc etc Pero en la práctica es simplemente más fácil calcular directamente el valor p. De vuelta en los “viejos tiempos”, lo que haríamos es abrir un libro de texto de estadísticas o algo así y pasar a la sección posterior que en realidad tendría una enorme tabla de búsqueda... así es como “calcularíamos” nuestro valor p, porque es demasiado esfuerzo hacerlo de otra manera. Sin embargo, como tenemos acceso a R, usaré la función pf () para hacerlo en su lugar. Ahora bien, ¿recuerdas que antes te expliqué que la prueba F siempre es unilateral? ¿Y que solo rechazamos la hipótesis nula para valores F muy grandes? Eso significa que solo nos interesa la cola superior de la distribución F. El comando que usarías aquí sería este...
pf( 18.6, df1 = 2, df2 = 15, lower.tail = FALSE)## [1] 8.672727e-05Por lo tanto, nuestro valor p llega a 0.0000867, o 8.67×10 −5 en notación científica. Entonces, a menos que estemos siendo extremadamente conservadores sobre nuestra tasa de error Tipo I, estamos prácticamente garantizados para rechazar la hipótesis nula.
En este punto, básicamente terminamos. Habiendo completado nuestros cálculos, es tradicional organizar todos estos números en una tabla ANOVA como la de Tabla @reftab:anovatable. Para nuestros datos de ensayos clínicos, la tabla ANOVA se vería así:
| df | suma de cuadrados | cuadrados medios | Estadístico F | valor p | |
|---|---|---|---|---|---|
| entre grupos | 2 | 3.45 | 1.73 | 18.6 | 8.67×10 −5 |
| dentro de grupos | 15 | 1.39 | 0.09 | - | - |
En estos días, probablemente nunca tendrás muchas razones para querer construir una de estas tablas tú mismo, pero encontrarás que casi todo el software estadístico (R incluido) tiende a organizar la salida de un ANOVA en una tabla como esta, por lo que es una buena idea acostumbrarse a leerlas. Sin embargo, aunque el software generará una tabla ANOVA completa, casi nunca hay una buena razón para incluir toda la tabla en tu escritura. Una forma bastante estándar de reportar este resultado sería escribir algo como esto:
El ANOVA de una vía mostró un efecto significativo del fármaco sobre la ganancia del estado de ánimo (F (2,15) =18.6, p<.001).
Suspiro. Tanto trabajo por una frase corta.


