15.3: Regresión Lineal Múltiple

El modelo de regresión lineal simple que hemos discutido hasta este punto asume que hay una única variable predictora que te interesa, en este caso dan.sleep. De hecho, hasta este punto, cada herramienta estadística de la que hemos hablado ha asumido que su análisis utiliza una variable predictora y una variable de resultado. Sin embargo, en muchos (quizás la mayoría) proyectos de investigación en realidad tienes múltiples predictores que quieres examinar. Si es así, sería bueno poder extender el marco de regresión lineal para poder incluir múltiples predictores. ¿Quizás algún tipo de modelo de regresión múltiple estaría en orden?

La regresión múltiple es conceptualmente muy simple. Todo lo que hacemos es agregar más términos a nuestra ecuación de regresión. Supongamos que tenemos dos variables que nos interesan; quizás queremos usar tanto dan.sleep como baby.sleep para predecir la variable dan.grump. Como antes, dejamos que Y _i se refiera a mi maldad en el día i-ésimo. Pero ahora tenemos dos variables X: la primera correspondiente a la cantidad de sueño que obtuve y la segunda correspondiente a la cantidad de sueño que mi hijo consiguió. Entonces dejaremos que X _i1 se refiera a las horas que dormí el día i-ésimo, y X _i2 se refiere a las horas que el bebé durmió ese día. Si es así, entonces podemos escribir nuestro modelo de regresión así:

Y _i = b ₂ X _i2 + b ₁ X _i1 + b ₀ + _i

Como antes, i es el residual asociado a la i-ésima observación,\(\ \epsilon_i = Y_i - \hat{Y_i}\). En este modelo, ahora tenemos tres coeficientes que necesitan ser estimados: b ₀ es la intercepción, b ₁ es el coeficiente asociado a mi sueño, y b ₂ es el coeficiente asociado con el sueño de mi hijo. Sin embargo, aunque el número de coeficientes que deben estimarse ha cambiado, la idea básica de cómo funciona la estimación no cambia: nuestros coeficientes estimados\(\ \hat{b_0}\),\(\ \hat{b_1}\) y\(\ \hat{b_2}\) son aquellos que minimizan la suma de los residuos cuadrados.

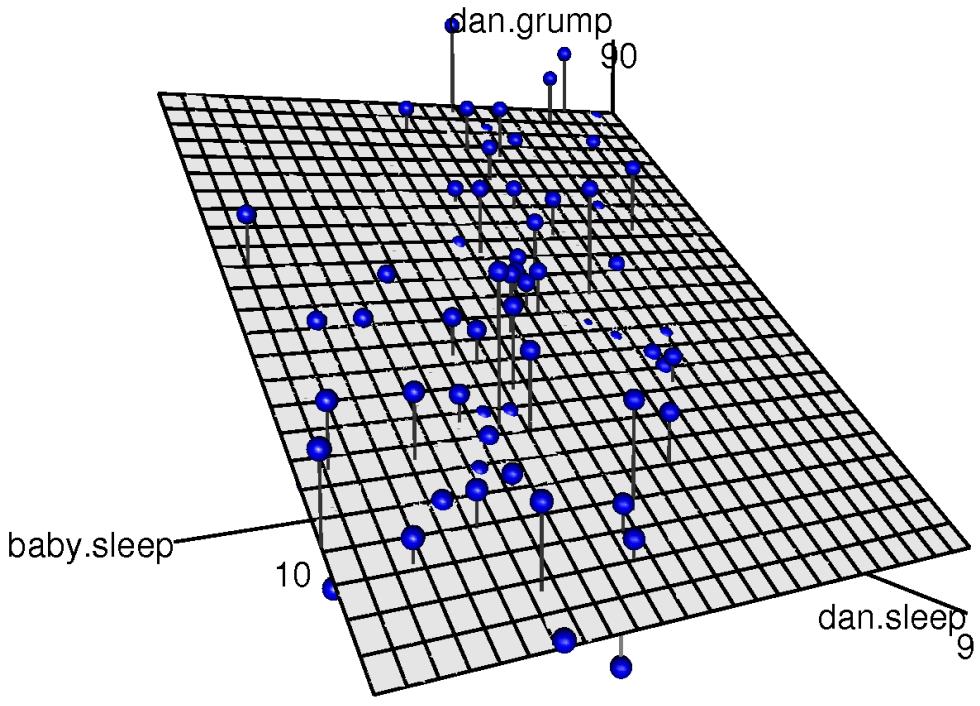
Figura 15.6: Visualización 3D de un modelo de regresión múltiple. Hay dos predictores en el modelo, dan.sleep y baby.sleep; la variable de resultado es dan.grump. Juntas, estas tres variables forman un espacio 3D: cada observación (puntos azules) es un punto en este espacio. De la misma manera que un modelo de regresión lineal simple forma una línea en el espacio 2D, este modelo de regresión múltiple forma un plano en el espacio 3D. Cuando estimamos los coeficientes de regresión, lo que estamos tratando de hacer es encontrar un plano que esté lo más cerca posible de todos los puntos azules.

Haciéndolo en R

La regresión múltiple en R no es diferente a la regresión simple: todo lo que tenemos que hacer es especificar una fórmula más complicada al usar la función lm (). Por ejemplo, si queremos usar tanto dan.sleep como baby.sleep como predictores en nuestro intento de explicar por qué estoy tan gruñón, entonces la fórmula que necesitamos es esta:

   dan.grump ~ dan.sleep + baby.sleep

Observe que, al igual que la última vez, no he incluido explícitamente ninguna referencia al término de intercepción en esta fórmula; solo las dos variables predictoras y el resultado. Por defecto, la función lm () asume que el modelo debe incluir una intercepción (aunque puedes deshacerte de ella si quieres). En cualquier caso, puedo crear un nuevo modelo de regresión —al que llamaré regression.2 — usando el siguiente comando:

regression.2 <- lm( formula = dan.grump ~ dan.sleep + baby.sleep,  
                     data = parenthood )

Y al igual que la última vez, si imprimimos () este modelo de regresión podemos ver cuáles son los coeficientes de regresión estimados:

print( regression.2 )

## 
## Call:
## lm(formula = dan.grump ~ dan.sleep + baby.sleep, data = parenthood)
## 
## Coefficients:
## (Intercept)    dan.sleep   baby.sleep  
##   125.96557     -8.95025      0.01052

El coeficiente asociado con dan.sleep es bastante grande, lo que sugiere que cada hora de sueño que pierdo me hace mucho más gruñón. Sin embargo, el coeficiente para bebé.dormir es muy pequeño, lo que sugiere que realmente no importa cuánto duerma mi hijo; no realmente. Lo que importa en lo que va mi maldad es lo mucho que duermo. Para tener una idea de cómo se ve este modelo de regresión múltiple, la Figura 15.6 muestra una gráfica 3D que traza las tres variables, junto con el modelo de regresión en sí.

Fórmula para el caso general

La ecuación que di arriba te muestra cómo se ve un modelo de regresión múltiple cuando incluyes dos predictores. No es sorprendente, entonces, si quieres más de dos predictores todo lo que tienes que hacer es agregar más términos X y más coeficientes b. En otras palabras, si tiene K variables predictoras en el modelo, entonces la ecuación de regresión se ve así:

\(Y_{i}=\left(\sum_{k=1}^{K} b_{k} X_{i k}\right)+b_{0}+\epsilon_{i}\)