2.4: Gráficas de Datos Categóricos
- Page ID
- 151653
Al describir datos categóricos con gráficas, queremos poder visualizar la diferencia en proporciones o porcentajes dentro de cada grupo. Estos valores también se conocen como frecuencias relativas.
Definición: Frecuencia relativa
n = tamaño de la muestra ‐ El número de observaciones en el tamaño de su muestra.
Frecuencia ‐ el número de veces que se observa un valor particular.
Frecuencia relativa ‐ La proporción o porcentaje de veces que se observa un valor particular.
Frecuencia relativa = Frecuencia/n
Ejemplo: Una variable categórica ‐ estado civil
Se tomó una muestra de 500 adultos (mayores de 18 años) del condado de Santa Clara, California, del Censo de Estados Unidos del año 2000. 14 Los resultados se muestran en la tabla:
| Estado civil | Frecuencia | Frecuencia relativa |
|---|---|---|
| Casado | 270 | 270/500 = 0.540 o 54.0% |
| Viudo | 22 | 22/500 = 0.044 o 4.4% |
| Divorciado ‐ no vuelto a casarse | 42 | 42/500 = 0.084 o 8.4% |
| Separados | 10 | 10/500 = 0.020 o 2.0% |
| Soltero ‐ nunca casado | 156 | 156/500 = 0.312 o 31.2% |
| Total | 500 | 500/500 = 1.000 o 100.0% |
Solución
Análisis ‐ más de la mitad de los adultos muestreados fueron reportados como casados. El grupo más pequeño fue separado, lo que representó solo 2% de la muestra.
Ejemplo: Comparando dos variables categóricas: aprobación presidencial y género
Reuters/Ipsos realiza una encuesta diaria de seguimiento de adultos estadounidenses para evaluar el apoyo del presidente de Estados Unidos. Estos son los resultados de una encuesta de seguimiento que finalizó el 17 de agosto de 2017, que incluye datos de los cinco días en los que Donald Trump hizo varias declaraciones altamente polémicas sobre la violencia luego de una reunión de neonazis y supremacistas blancos en Charlottesville, Virginia. La pregunta es “En general, ¿aprueban o desaprueban la forma en que Donald Trump está manejando su trabajo como presidente?” 15
| Frecuencia Hembra | Frecuencia Masculina | Frecuencia Relativa Femenina | Frecuencia Relativa Masculina | |
|---|---|---|---|---|
| Aprobar | 392 | 404 | 0.295 o 29.5% | 0.400 o 40.0% |
| Desaprobar | 846 | 545 | 0.634 o 63.4% | 0.541 o 54.1% |
| Insegura/Sin Opinión | 96 | 59 | 0.079 o 7.9% | 0.059 o 5.9% |
| Total | 1334 | 1008 | 1.000 o 100% | 1.000 o 100% |
Solución
Análisis — Tanto hombres como mujeres desaprobaron la forma en que Donald Trump manejaba su trabajo como presidente en la fecha de la encuesta. Las mujeres tuvieron una mayor tasa de desaprobación que los hombres. En la ciencia política, esto se llama brecha de género.
Gráficos de Barras
Una forma de representar datos categóricos es en un gráfico de barras, donde la altura de la barra puede representar la frecuencia o frecuencia relativa de cada elección.
Las gráficas siguientes representan la información del estado civil del ejemplo categórico. El eje vertical en la primera gráfica muestra frecuencias para cada grupo, mientras que la segunda gráfica muestra las frecuencias relativas (mostradas aquí como porcentajes).
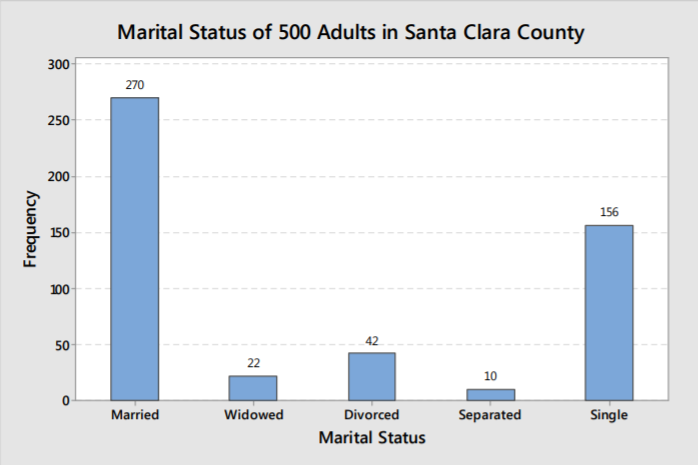
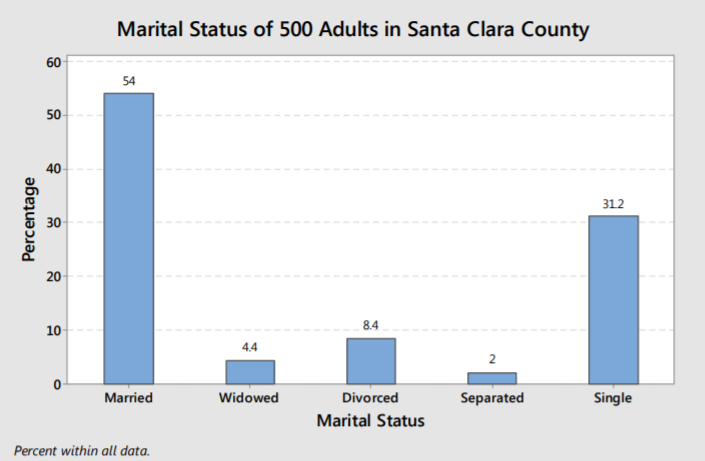
No hay diferencia en la forma de cada gráfica ya que el porcentaje o frecuencia en cada grupo es directamente proporcional al área de cada barra.
En cualquier caso, podemos hacer el mismo análisis, que casados y solteros son los estados conyugales que ocurren con mayor frecuencia.
Se puede utilizar un gráfico de barras agrupado para comparar variables categóricas, como la encuesta de aprobación presidencial tabulada por género. Se puede ver en esta gráfica que las mujeres tienen una desaprobación mucho más fuerte de Trump que los hombres. En esta gráfica, el eje vertical es la frecuencia, pero también se podría hacer que el eje vertical sea frecuencia o porcentaje relativo.
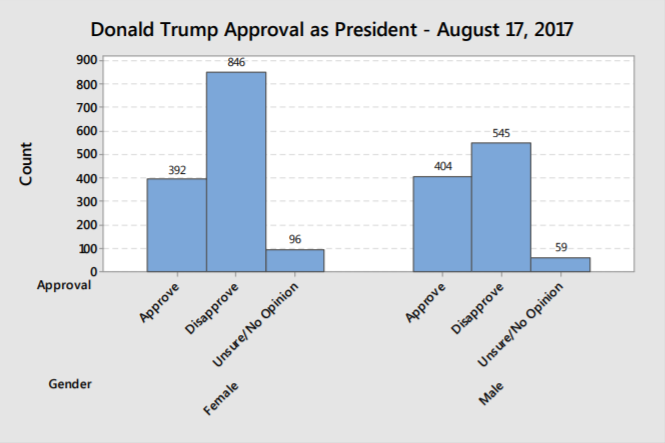
Otra forma de representar los mismos datos es un gráfico de barras apiladas, que se muestra aquí con porcentaje (frecuencia relativa) como eje vertical. Es más difícil ver la diferencia entre hombres y mujeres, pero los porcentajes totales de aprobación/desaprobación son más fáciles de leer.
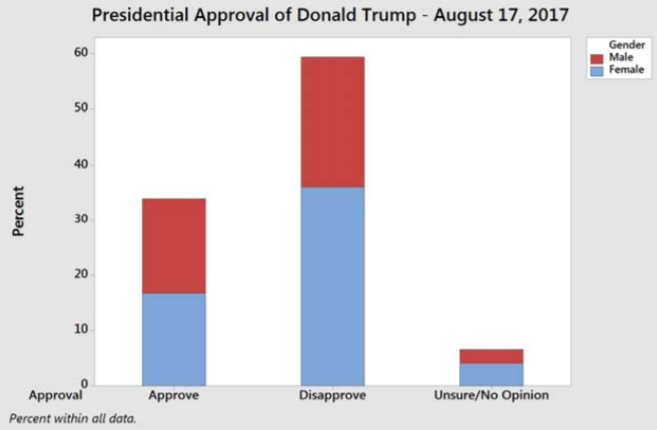
Ejemplo: Brechas históricas de género
Aquí hay otro gráfico de barras agrupado reportado por ABC News, el 21 de agosto, que muestra que Trump tenía una brecha de género mayor que los dos presidentes anteriores, Barack Obama y George W. Bush. 16
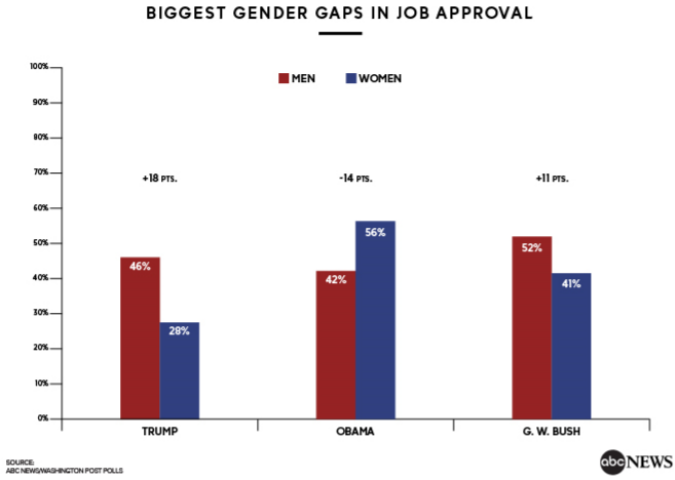
En conclusión, los gráficos de barras son una excelente manera de mostrar, analizar y comparar datos categóricos. No obstante, se debe tener cuidado para no crear gráficas engañosas.
Ejemplo: Inscripción mal reportada a la Ley del Cuidado de
Aquí un ejemplo de un gráfico de barras reportado en el canal Fox News que distorsionó la verdad sobre las personas que se inscribieron en la Ley del Cuidado de Salud Asequible (ACA) en 2014, según informó mediamatters.org 17
El 27 de marzo la inscripción al seguro de salud a través de las bolsas de la ACA superó los 6 millones, superando la estimación revisada de inscritos para el primer año del programa antes de la fecha límite de inscripción abierta del 31 de marzo. La inscripción parece encaminada a alcanzar la estimación inicial de la Oficina de Presupuesto del Congreso de 7 millones de inscripciones, y teniendo en cuenta a los inscritos en Medicaid, la ACA habría extendido la cobertura de atención médica a al menos 9.5 millones de personas que antes no tenían seguro.
Fox celebró el último día de inscripción abierta al intentar torcer de alguna manera la reciente oleada de inscripciones en malas noticias para la ley.
America's Newsroom emitió un gráfico de barras extremadamente sesgado que hizo parecer que los 6 millones de inscritos comprendían aproximadamente un tercio de la meta de 7 millones de inscritos:
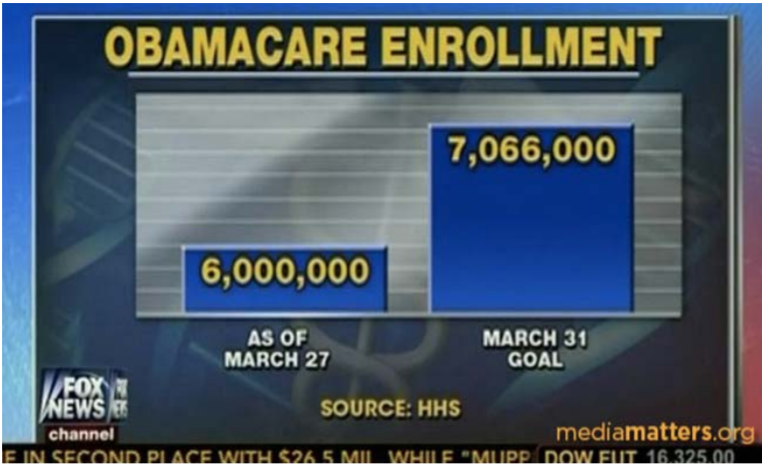
A primera vista, la gráfica aparentemente muestra que la matrícula ACA estaba muy por debajo de la meta proyectada. La gráfica es engañosa por tres razones:
- El eje vertical no inicia en cero inscritos, exagerando en gran medida la diferencia entre los dos números.
- El gráfico de los “6,000,000” inscritos no logró incluir a los nuevos inscritos en Medicaid, que formaba parte de la “Meta del 31 de marzo”.
- La inscripción reportada fue 4 días antes de la fecha límite. Al igual que los estudiantes haciendo sus tareas, mucha gente esperó hasta el último día para inscribirse.
Los números reales de matrícula superaron con creces la meta, exactamente lo contrario de este gráfico de barras mal construido.
Gráficos circulares
Otra forma de representar datos categóricos es un gráfico circular, en el que cada porción del pastel representa la frecuencia relativa o porcentaje de datos en cada categoría.
El gráfico circular que se muestra aquí representa el estado civil de 500 adultos en el condado de Santa Clara tomado del censo 200, los mismos datos que fueron representados por una gráfica de barras en un ejemplo anterior.
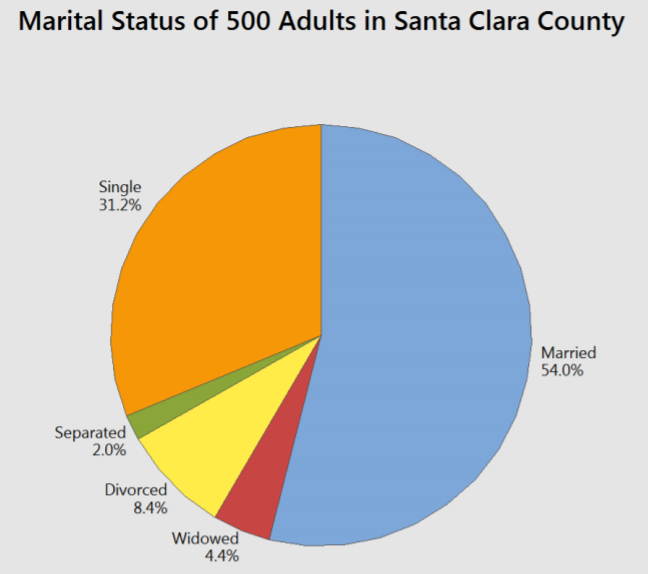
El análisis muestra nuevamente que la mayoría de las personas están casadas, seguidas de solteras.
Se puede usar un gráfico circular múltiple para comparar el efecto de una variable categórica sobre otra.
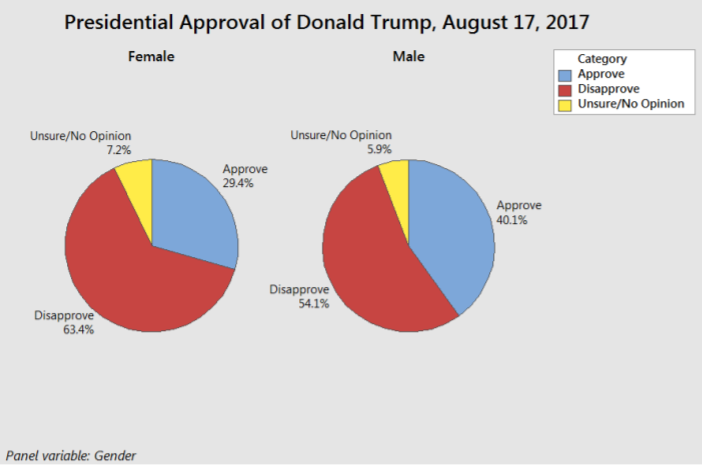
En el ejemplo de la encuesta de aprobación presidencial, un mayor porcentaje de mujeres adultas desaprueba el desempeño de Donald Trump como presidente de Estados Unidos en comparación con los adultos varones. Esto es comparable a los gráficos de barras apilados o agrupados mostrados en el ejemplo anterior.


