3.1: Medidas de Tendencia Central

Última actualización
Guardar como PDF

Page ID: 151767

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Comencemos esta sección con un ejemplo y una pregunta de opción múltiple:

Ejemplo: Entrega de pizza

Anthony's Pizza, una empresa con sede en Detroit, ofrece entrega de pizza a sus clientes. Un chofer de Anthony's Pizza a menudo hará varias entregas en una sola entrega. Una muestra de 5 entregas realizadas por un chofer mostró el número total de pizzas entregadas en cada tirada: ²³

2 2 5 9 12

¿Cuál es el número “promedio” de pizzas enviadas en una entrega a domicilio?

2 pizzas
5 pizzas
6 pizzas

Elige lo que creas que es la respuesta y volveremos a este ejemplo y discutiremos la respuesta al final de esta sección.

Media de la Muestra

La media muestral es la media aritmética de los valores de los datos. Simplemente suma todos los números y divide por el tamaño de la muestra. El símbolo$\bar{X}$ (pronunciado X‐bar) se refiere a la media de la muestra.

Definición: Media de la Muestra

Si$X_{1}, X_{2}, \cdots, X_{n}$ representa una muestra de tamaño$n$, entonces la media de la muestra es:

\[\bar{X}=\dfrac{X_{1}+X_{2}+\cdots+X_{n}}{n}=\dfrac{\sum X_{i}}{n} \nonumber\]

Para los datos Ejemplo - Entrega de pizza, la media de la muestra es$\bar{X}=\dfrac{2+2+5+9+12}{5}=6$ pizzas (el valor medio).

Mediana de la muestra

La mediana de la muestra es el valor que representa la mitad exacta de los datos, cuando los valores se ordenan de menor a mayor.

Procedimiento para encontrar la mediana muestral

Ordenar los valores de datos de menor a mayor.
Si hay un número impar de valores, la mediana de la muestra es el valor medio. \[\text { The median of }\{1,3,8,13,14\} \text { is } 8 \nonumber \]
Si hay un número par de valores, la mediana de la muestra es la media de los 2 valores medios\[\text { The median of }\{1,3,8,10,13,14\} \text { is } \dfrac{8+10}{2}=9 \nonumber \]

Ejemplo: Entrega de pizza

Para los datos de entrega de pizza {2, 2, 5, 9, 12}, la mediana de la muestra es de 5 pizzas (el valor medio).

Ejemplo: Precios de viviendas en un solo barrio

Aquí están los precios de venta de 6 viviendas en el mismo barrio en Antioch, California ²⁴:

$500,000 $550,000 $600,000 $700,000 $700,000 $1,950.000

La media muestral es $1,000,000 (sumar los valores y dividir por 5).

La mediana muestral es de $650,000 ($600,000 más $700,000 divididos por 2).

¿Cuál de los dos valores es una mejor medida del hogar “promedio” en este barrio?

Aquí la mediana muestral es una mejor medida del centro, porque $650,000 mejor representa un hogar típico en este barrio. La media no es una buena medida de centro aquí porque el valor de la vivienda atípica, que cuesta $1,950.000. La mediana nunca se verá afectada por valores atípicos porque es solo la ubicación lo que importa a la hora de calcular la mediana.

A diferencia de la media, la mediana (que se basa en la clasificación en lugar de valores), puede calcularse para datos categóricos ordinales, pero no para datos nominales.

Ejemplo: Calificaciones en una clase de matemáticas

En una clase de álgebra de colegio comunitario, un instructor entregó las siguientes calificaciones a 40 alumnos. Determinar la mediana de la nota para el curso.

El primer paso es ordenar las calificaciones de menor a mayor:

Los valores medios son ambos B, por lo que el grado medio es B.

Modo de muestra

El modo de muestra es el valor que ocurre con mayor frecuencia en los datos. Si hay múltiples valores que ocurren con mayor frecuencia, entonces hay múltiples modos en los datos.

Ejemplo: Entrega de pizza

Para los datos de entrega de pizza {2, 2, 5, 9, 12}, el modo de muestra es de 2 pizzas porque 2 ocurre con mayor frecuencia en los datos.

Volvamos ahora a la pregunta original al inicio de esta sección.

¿Cuál es el número “promedio” de pizzas enviadas en una entrega a domicilio?

2 pizzas
5 pizzas
6 pizzas

Ya que 2 es el modo, 5 es la mediana y 6 es la media, prácticamente hablando las 3 respuestas son ejemplos de “promedios”. Lightbulb Books llama humorísticamente a estas estadísticas “Los osos promedio”. ²⁵

Muchos (incluyendo algunos textos de Estadísticas) asumirán automáticamente que el promedio es lo mismo que la media. En la vida general, las personas usarán los términos media y promedio indistintamente. Pero en Estadística, cuando usamos la palabra “promedio”, nos referimos a un valor que representa el centro de los datos. Hay muchas estadísticas que representan el centro de los datos, incluyendo la media, mediana y modo.

El modo también se puede utilizar para datos categóricos nominales y ordinales.

Ejemplo: Datos nominales ‐ Estado civil

Volvamos a la muestra de 500 adultos (mayores de 18 años) del condado de Santa Clara tomada del Censo de Estados Unidos del año 2000.

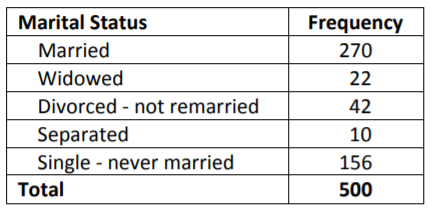
El modo para estos datos es valor con la frecuencia más alta, “Casado”.

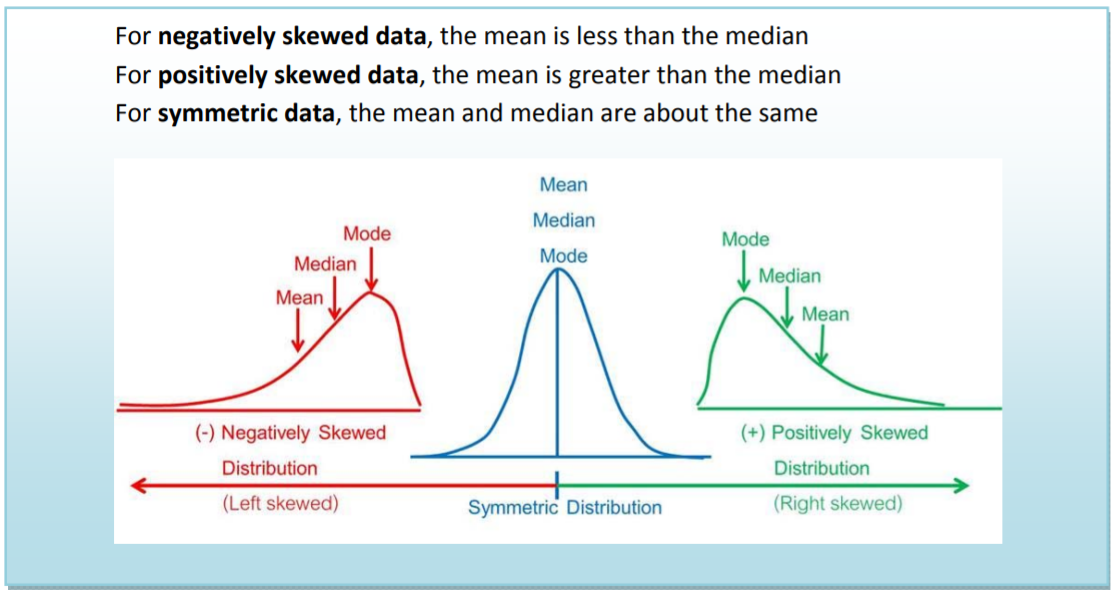
Usar la media y la mediana para determinar la asimetría

La asimetría es una medida de cuán asimétricos son los vales de datos. Los datos pueden estar sesgados positivamente (estirados hacia la derecha), sesgados negativamente (estirados hacia la izquierda) o simétricos (sin asimetría). Ahora vamos a explorar qué efecto tiene la asimetría en las medidas de centro con varios ejemplos.

Ejemplo: Datos simétricos — Alturas de hombres

Aquí hay una gráfica de puntos y estadísticas resumidas de las alturas en pulgadas de 1000 hombres, de 30 años

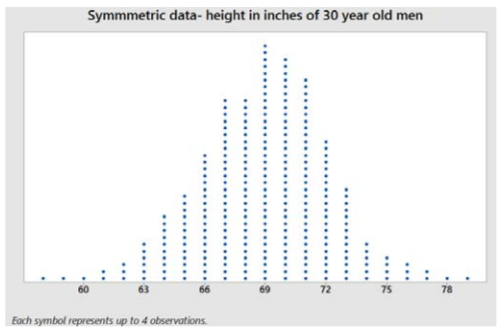
Media de la muestra = 68.98 pulgadas

Mediana de la muestra = 69 pulgadas

Modo de muestra = 69 pulgadas

Los valores de los datos se distribuyen uniformemente a la derecha e izquierda del pico. Cuando los datos son simétricos, la media, la mediana y el modo son aproximadamente los mismos.

Ejemplo: Datos positivamente sesgados — Redwood trees

Aquí hay una gráfica de puntos y estadísticas resumidas de la edad de 1000 secuoyas muestreadas en parques de California.

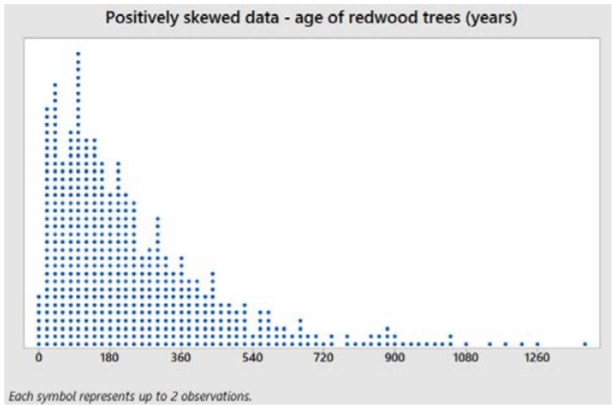
Media de la muestra = 237.48 años

Mediana de la muestra = 180 años

Modo de muestreo = 100 años

Los valores de los datos se estiran a la derecha del centro, haciendo que la media sea mayor que la mediana. Además, la mediana generalmente será mayor que el modo para datos sesgados positivamente.

Ejemplo: Datos sesgados negativamente — Calificaciones del examen

Aquí hay una gráfica de puntos y estadísticas resumidas de la calificación porcentual de 1000 exámenes de mitad de período impartidos por un instructor de matemáticas a estudiantes de álgebra.

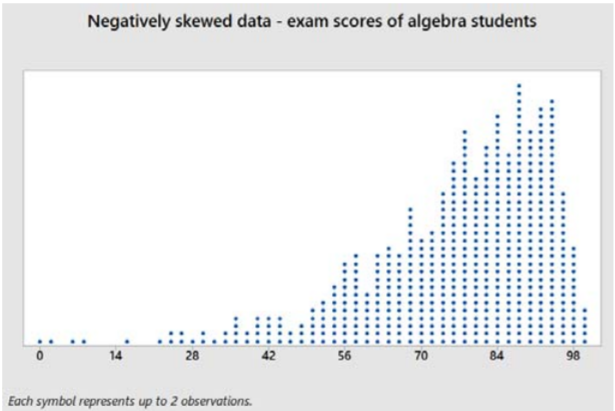
Media de la muestra = 76.21

Mediana de la muestra = 80

Modo de muestreo = 91

Los valores de los datos se estiran a la izquierda del centro, haciendo que la media sea menor que la mediana. Además, la mediana generalmente será menor que el modo para los datos sesgados negativamente.

Usando la media y la mediana para encontrar asimetría en los datos ²⁶

Ejemplo: Estudiantes navegando por la web

A partir de un ejemplo anterior, esta gráfica de tallo y hoja representa cuánto tiempo pasaron 30 estudiantes en un navegador web (en Internet) en un periodo de 24 horas. Los datos se redondean al minuto más cercano.

\ [\ begin {array} {ll}
6 & 7\\
7 & 18\\
8 & 25677\\
9 & 25799\\
10 & 01233455789\\
11 & 268\\
12 & 245
\ end {array}\ nonumber\]

La mediana muestral es de 101.5 minutos, ya que la 15ª observación es 101 y la 16ª observación es 102.

Dado que los datos son negativos sesgados, esperaríamos que la media de la muestra sea menor que la mediana de la muestra.

Sumando los valores y dividiendo por 30, calculamos que la media muestral es 96.6 minutos, consistente con valores de datos que están sesgados negativamente.

Tenga en cuenta que el modo no es útil en este ejemplo ya que el tamaño de la muestra es pequeño.

Media de la Muestra

Mediana de la muestra

Modo de muestra

Usar la media y la mediana para determinar la asimetría

Usando la media y la mediana para encontrar asimetría en los datos 26

Usando la media y la mediana para encontrar asimetría en los datos ²⁶