3.5: Trabajar con valores atípicos
- Page ID
- 151781
Un valor atípico es un punto de datos que está muy alejado de las otras entradas del conjunto de datos. Los valores atípicos podrían ser causados por:
- Errores cometidos en la grabación de datos
- Datos que no pertenecen a la población
- Verdaderos eventos raros
Los dos primeros casos son sencillos de tratar ya que podemos corregir errores o eliminar datos que no pertenecen a la población. El tercer caso es más problemático ya que los valores atípicos extremos aumentarán drásticamente la desviación estándar y sesgarán fuertemente los datos.
En El cisne negro, Nicholas Taleb sostiene que algunas poblaciones con valores atípicos extremos no deben analizarse con intervalos de confianza tradicionales y pruebas de hipótesis. 30 Define a un Cisne Negro como un valor atípico extremo impredecible que causa efectos dramáticos en la población. Un ejemplo reciente de Cisne Negro fue la catastrófica caída en el valor de las inversiones no reguladas de seguros inmobiliarios de Credit Default Swap (CDS) que provocó el casi colapso del sistema bancario internacional en 2008. El análisis estadístico tradicional que midió el riesgo de las inversiones de CDS no tomó en cuenta la consecuencia de un rápido incremento en el número de ejecuciones hipotecarias de viviendas. En este caso, las estadísticas que miden el desempeño de la inversión y el riesgo fueron inútiles y crearon una falsa sensación de seguridad para los grandes bancos y compañías de seguros.
Ejemplo: ventas de casas inmobiliarias
Aquí están las ventas trimestrales de viviendas para 10 inmobiliarias: 2 2 3 4 5 5 6 6 7 50
| Con valores atípicos | Sin valores atípicos | |
|---|---|---|
| Media | 9.00 | 4.44 |
| Mediana | 5.00 | 5.00 |
| Desviación estándar | 14.51 | 1.81 |
| Intercuartil | 3.00 | 3.50 |
En este ejemplo, el número 50 es un valor atípico. Al calcular las estadísticas resumidas, podemos ver que la media y la desviación estándar se ven dramáticamente afectadas por el valor atípico, mientras que la mediana y el rango intercuartílico (que se basan en el ranking de los datos) apenas cambian. Una solución cuando se trata de una población con valores atípicos extremos es utilizar estadísticas inferenciales que utilicen los rangos de los datos, también llamados estadísticas no paramétricas.
Usando Box Plot para encontrar valores atípicos
- La “caja” es la región entre los cuartiles 1 y 3.
- Los posibles valores atípicos son más de 1.5 IQR de la caja (cerca interior)
- Los valores atípicos probables son más de 3 IQR de la caja (cerca exterior)
- En la gráfica de caja a continuación del ejemplo de agente inmobiliario, las líneas punteadas representan las “cercas” internas y externas que son 1.5 y 3 IQR respectivamente de la caja. Vea cómo el punto de datos 50 está bien fuera de la cerca exterior y por lo tanto un valor atípico casi seguro.
- Los bigotes ahora terminan en el valor más extremo que NO es un posible valor atípico.
Cerca Interior Inferior = Q1 — (1.5) IQR = 3 — (1.5) (3) = ‐1.5
Cerca Exterior Inferior = Q1 — (3) IQR = 3 — (3) (3) = ‐6
Valla Interior Superior = Q3 + (1.5) IQR = 6 + (1.5) (3) = 10.5
Valla Exterior Superior = Q3 + (3) IQR = 6 + (3) (3) = 15
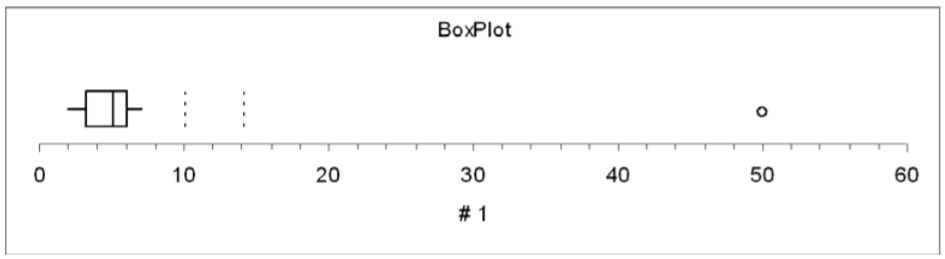
Dado que el valor 50 está mucho más allá de la cerca exterior de 15, 50 es un valor atípico extremo.
Pasos para hacer una parcela de caja (con valores atípicos)
- Dibuja la caja entre Q1 y Q3
- Trazar con precisión la mediana
- Determinar posibles valores atípicos que son más de 1.5 rangos intercuartílicos a partir de la caja.
Cerca Interior Inferior = Q1 — (1.5) IQR
Cerca Interior Superior = Q3 + (1.5) IQR
- Marcar valores atípicos con un carácter especial como un * o •.
- Dibuja bigotes a valores mínimos y máximos que no sean valores atípicos posibles.
(nota: diagrama de caja abajo no dibujado a escala)

Ejemplo: Comparando manzanas con naranjas
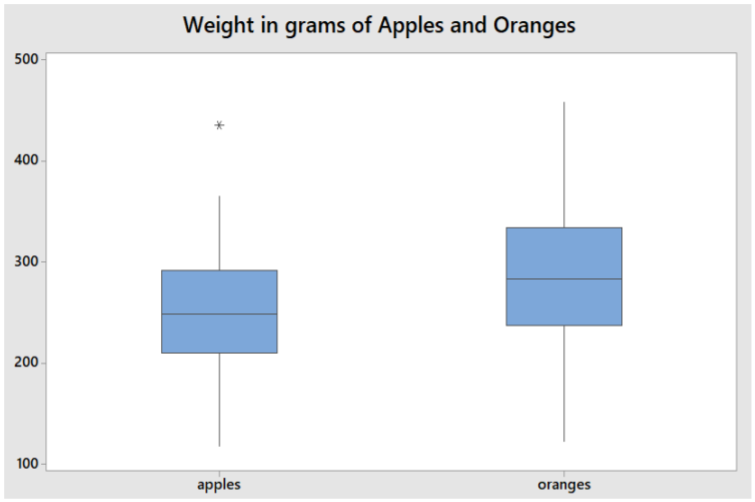
Usando las estadísticas resumidas, haga parcelas de caja lado a lado de los pesos de 100 manzanas Fuji y 100 naranjas ombligo. Analizar e interpretar las gráficas, incluyendo los valores atípicos.
Resumen de Estadísticas:
| Variable | Fruto | N | Mínimo | Q1 | Mediana | Q3 | Máximo | IQR |
|---|---|---|---|---|---|---|---|---|
| pesos | manzanas | 100 | 118.00 | 210.00 | 248.00 | 291.50 | 435.00 | 81.50 |
| naranjas | 100 | 122.00 | 237.25 | 283.50 | 333.50 | 458.00 | 96.25 |
Solución
Las naranjas tienen una mediana de peso mayor en comparación con las manzanas.
El IQR es un poco más grande para las naranjas.
Ambos frutos tienen gráficas que son en su mayoría simétricas.
La manzana que pesa 435 gramos es un posible valor atípico ya que el peso supera la Valla Interior = 291.50 + 1.5 (81.5) = 414.
El siguiente peso más alto de manzana es de 365 gramos.
Usar la puntuación z para encontrar valores atípicos
El puntaje z también se puede usar para encontrar valores atípicos, pero se debe tener cuidado ya que la media y la desviación estándar se ven afectadas por valores atípicos. Una estrategia es eliminar el valor atípico antes de calcular estas estadísticas.
Procedimiento para usar z‐score para encontrar valores atípicos
- Calcular la media de la muestra y la desviación estándar sin el valor atípico sospechoso.
- Calcular la puntuación Z del valor atípico sospechoso:\(z-\text { score }=\dfrac{X_{i}-\bar{X}}{s}\)
- Si la puntuación Z es mayor que 3 o menor que ‐3, ese punto de datos es un valor atípico probable.
Ejemplo: ventas de casas inmobiliarias
Determinar si 50 es un valor atípico.
Solución
Determinar la media de la muestra y la desviación estándar excluyendo el valor 50. \[\bar{X}=4.44 \quad s=1.81 \nonumber \]
Determine la puntuación z para 50. \[z-\text { score }=\dfrac{50-4.4}{1.81}=25.2 \nonumber \]
Dado que 25.2 es mucho mayor que 3, el valor 50 es un valor atípico extremo
Valores atípicos, ¿qué hacer?
No hay una respuesta clara qué hacer con los valores atípicos legítimos. ¿Los quitamos o los dejamos adentro?
Para algunas poblaciones, los valores atípicos no cambian drásticamente el análisis estadístico general. Ejemplo: la persona más alta del mundo no cambiará drásticamente la estatura media de 10000 personas.
Sin embargo, para algunas poblaciones, un único valor atípico tendrá un efecto dramático en el análisis estadístico (llamado “Cisne Negro” por Nicholas Taleb 31), y las estadísticas inferenciales pueden ser inválidas al analizar estas poblaciones. Ejemplo: la persona más rica del mundo cambiará drásticamente la riqueza media de 10000 personas.


