3.6.1: Graficando Datos Bivariados con Gráficas de Dispersión
- Page ID
- 151807
Una gráfica de dispersión es una gráfica útil para buscar relaciones entre dos variables numéricas. Esta relación se llama correlación. Al realizar análisis de correlación, haga estas preguntas:
- ¿Cuál es la dirección de la correlación?
- ¿Cuál es la fuerza de la correlación?
- ¿Cuál es la forma de la correlación?
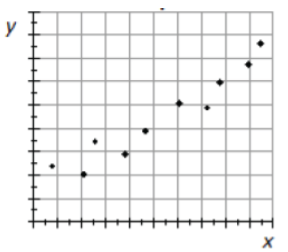
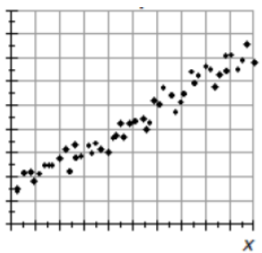
Ejemplo: Rendimiento de pepino y precipitación
Esta gráfica de dispersión representa datos recolectados aleatoriamente sobre la precipitación de la temporada de crecimiento y el rendimiento de pepino Es razonable sugerir que la cantidad de agua recibida en un campo durante la temporada de crecimiento influirá en el rendimiento de los pepinos que crecen en él. 32
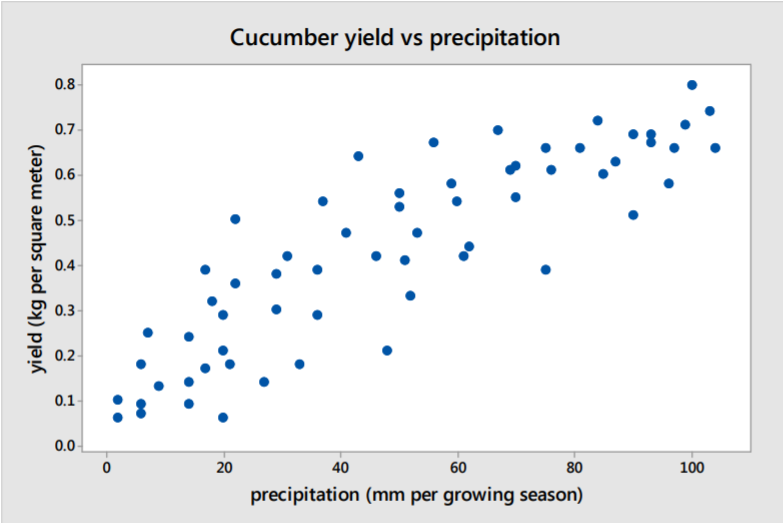
Solución
Dirección: La correlación es positiva, el rendimiento aumenta a medida que aumenta la precipitación.
Fuerza: Existe una correlación moderada a fuerte.
Forma: Mayormente lineal, pero puede haber una ligera curva descendente en el rendimiento a medida que aumenta la precipitación.
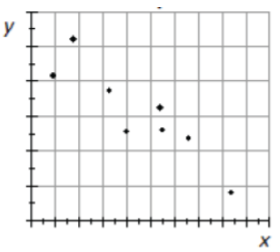
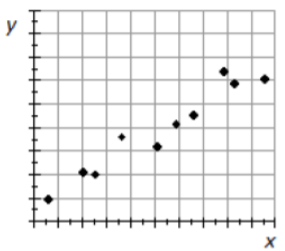
Ejemplo: GPA y clase faltante
Un grupo de estudiantes de Georgia College realizó una encuesta en la que se hacían varias preguntas a los estudiantes al azar sobre su perfil académico. Una parte de su estudio fue ver si existe alguna correlación entre el GPA de varios estudiantes y las clases perdidas. 33
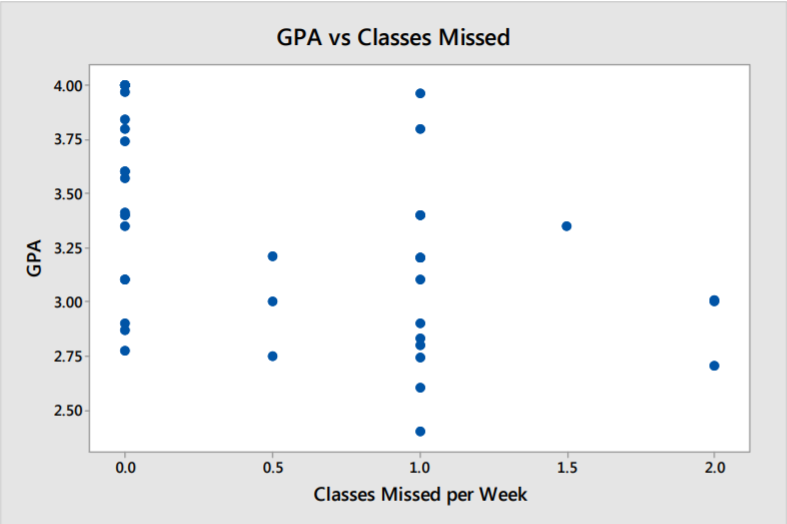
Solución
Dirección: La correlación, en su caso, es negativa. Tendencias de GPA más bajas para estudiantes que falten a más clases.
Fuerza: Hay una correlación muy débil presente.
Forma: Difícil de decir, pero un ajuste lineal no es irrazonable.
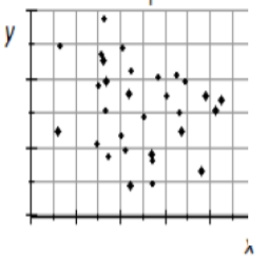
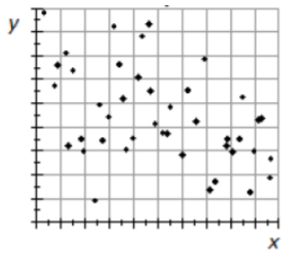
Ejemplo: Tiempos de viaje y temperatura
Un instructor de matemáticas viaja en automóvil desde su casa en San Francisco al Colegio De Anza en Cupertino, California. Durante 100 días seleccionados al azar durante el año, el instructor registró el tiempo de viaje y la temperatura en Cupertino al momento de su llegada.
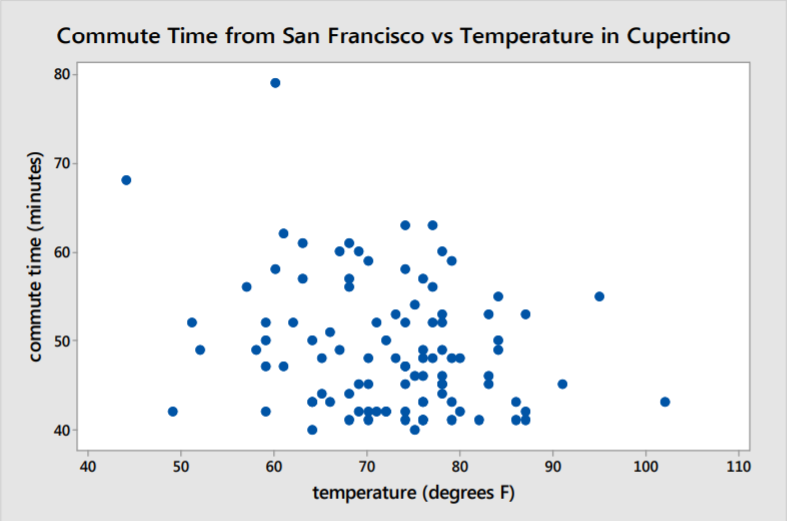
Solución
Dirección: No hay una dirección obvia presente.
Fuerza: No hay correlación aparente entre el tiempo de viaje y la temperatura.
Forma: Como no hay correlación aparente, buscar una forma no tiene sentido.
Otro: Hay dos valores atípicos que representan tiempos de viaje muy largos.
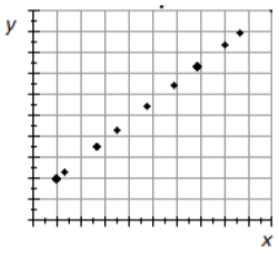
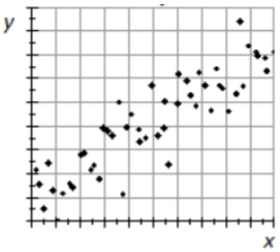
Ejemplo: Edad de los arces azucareros
¿Es posible estimar la edad de los árboles midiendo los diámetros de los troncos? Los datos fueron reconstruidos por un estudio integral realizado por el Departamento de Agricultura de Estados Unidos. Los investigadores recopilaron datos de arces azucareros de crecimiento antiguo en bosques del norte de Estados Unidos. 34
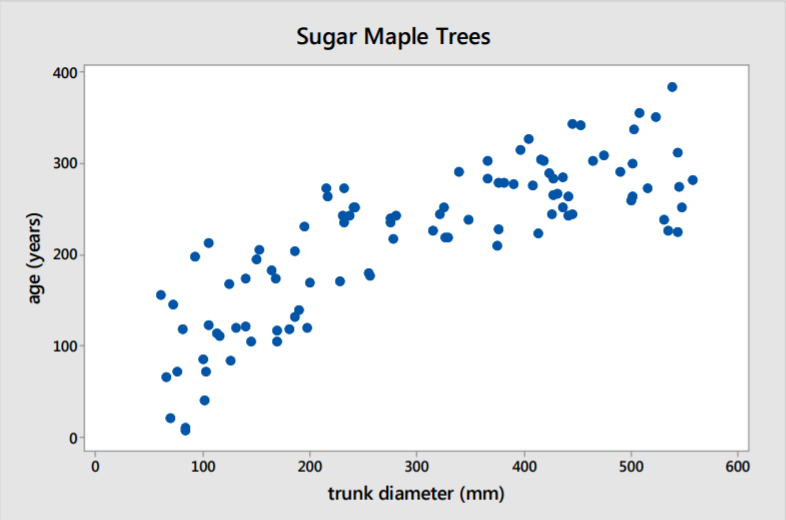
Solución
Dirección: Hay una correlación positiva presente. La edad aumenta conforme aumenta el tamaño del tronco.
Fuerza: La correlación es fuerte.
Forma: La forma de la gráfica es curva hacia abajo, lo que significa que la correlación no es lineal.
Ejemplo: posesión de armas y suicidios con armas
Esta trama dispersa representa la posesión de armas y los suicidios con armas de fuego para 73 países diferentes. Los datos se ajustan a las tasas por población para fines de comparación. 35
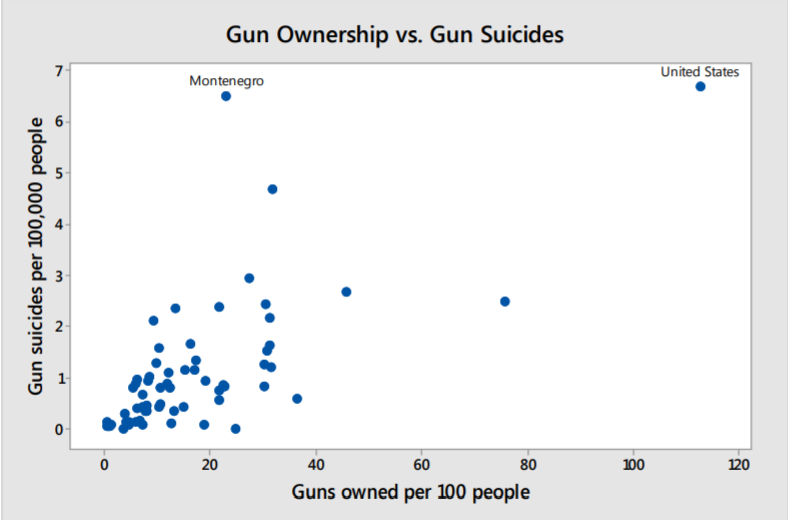
Solución
Dirección: Hay una correlación positiva presente. Más posesión de armas significa más suicidios con armas.
Fuerza: La correlación es moderada para la mayoría de los datos.
Forma: La forma de la gráfica es lineal para la mayoría de los datos.
Otro: Hay algunos valores atípicos en los que la posesión de armas es mucho mayor. También hay un valor atípico con una tasa de suicidios extremadamente alta.
Este último ejemplo demuestra que los valores atípicos pueden dificultar la lectura de gráficos. Por ejemplo, Estados Unidos tiene las tasas de propiedad de armas más altas y las tasas más altas de suicidio por arma de fuego entre estos países, lo que hace que Estados Unidos se encuentre lejos de la mayor parte de los datos en la trama de dispersión. Montenegro tuvo el segundo suicidio más alto por tasa de armas, pero con una tasa de propiedad de armas mucho menor.


