5.6: Probabilidad condicional

Última actualización
Guardar como PDF

Page ID: 151836

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Probabilidad condicional significa la probabilidad de que ocurra un evento A dado que ya ocurrió otro evento B. Esta probabilidad se escribe como\(P(A|B)\) que se lee como\(P(A \text{ given } B)\).

Ejemplo: elección presidencial de 2016

En las elecciones presidenciales de Estados Unidos de 2016, Donald Trump recibió 46% del total de votos, Hillary Clinton recibió 48%, y otros candidatos recibieron 6%. (Nota: aunque Clinton recibió alrededor de 3 millones de votos más que Trump, el Colegio Electoral determinó que el ganador real era Trump).

CNN realizó encuestas de salida para determinar cómo votaron las personas con base en estadísticas demográficas, como el género. ⁶⁴ Estas encuestas de salida mostraron que 53% de los votantes eran mujeres y 47% de los votantes eran varones. Estos dos valores son ejemplos de probabilidades marginales.

Las encuestas también mostraron que Donald Trump recibió el 41% del voto femenino y el 52% del voto masculino. Estos dos valores son ejemplos de probabilidad condicional, en los que la condición es conocer el género del elector.

Solución

Eventos	Probabilidades Marginales	Probabilidades condicionales
T = El votante elige a Trump	\(P(T)=0.46\)	\(P(T\|F) = 0.41\)
F = El elector es femenino	\(P(F) = 0.53\)	\(P(T\|M) = 0.52\)
M = El votante es masculino	\(P(M) = 0.47\)

Al calcular la probabilidad de A dada B, solo necesitamos considerar los elementos del Evento B en lugar de todo el espacio muestral.

Ejemplo: Cursos para estudiantes

Revisemos el ejemplo de estudiantes que toman Matemáticas e Historia. Supongamos que queríamos calcular la probabilidad de que un estudiante que está tomando matemáticas también esté tomando historia.

Solución

En este caso solo necesitamos considerar a los 40 estudiantes que toman las matemáticas como espacio de muestra y a los 10 estudiantes que toman tanto matemáticas como historia como el evento condicional que ocurre.

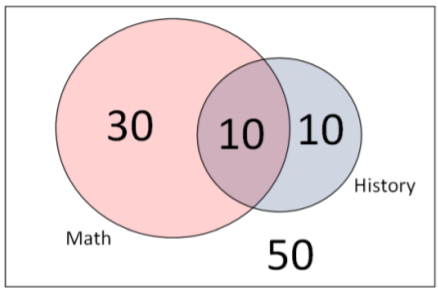
\(P(\text { History })=20 / 100=0.20\)

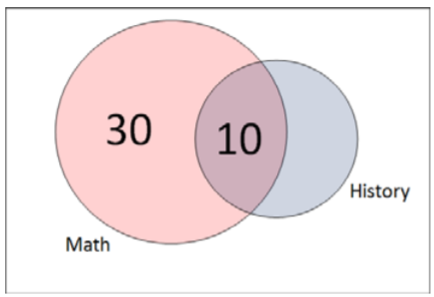
\(P(\text { History } \mid \text { Math })=10 / 40=0.25\)

En este ejemplo, utilizamos reglas clásicas de probabilidad de conteo, pero la probabilidad condicional se puede calcular directamente usando probabilidades marginales y condicionales conocidas.

Reglas para Probabilidad Condicional

\[P(A \mid B)=\dfrac{P(A \text { and } B)}{P(B)} \nonumber \]

\[P(B \mid A)=\dfrac{P(A \text { and } B)}{P(A)} \nonumber \]

Ejemplo: Portador de telefonía celular

De todos los usuarios de celulares en EU, 15% tiene un teléfono inteligente con AT&T. 25% de todos los usuarios de celulares usan AT&T Dado que un usuario de celular seleccionado tiene AT&T, encuentra la probabilidad de que el usuario también tenga un teléfono inteligente.

Solución

Let A = suscriptor de AT&T. Let B = Usuario de Teléfono Inteligente

\(P(A)=0.25 \quad P(A \text { and } B)=0.15\)

\(P(A \mid B)=\dfrac{0.15}{0.25}=0.60\)

Esto significa que el 60% de todos los suscriptores de AT&T tienen teléfonos inteligentes.