5.7: Tablas de contingencia (de dos vías)
- Page ID
- 151847
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Tablas de contingencia, también conocidas como tabulaciones cruzadas, tabulaciones cruzadas o tablas de dos vías, es un método para mostrar los recuentos de las respuestas de dos variables categóricas a partir de datos.
Ejemplo: Accidentes y DUI
Se les preguntó a 1000 conductores si estuvieron involucrados en un accidente en el último año. También se les preguntó si durante este tiempo, eran DUI, manejando bajo los efectos del alcohol o las drogas. Los totales se resumen en una tabla de contingencia:
| Accidente | Sin Accidente | Total | |
|---|---|---|---|
| DUI | 70 | 130 | 200 |
| No DUI | 30 | 770 | 800 |
| Total | 100 | 900 | 1000 |
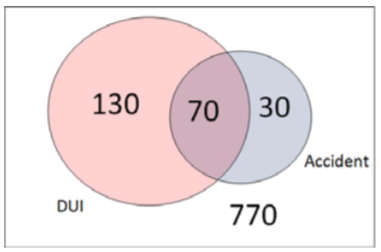
Solución
En la tabla, cada columna representa una opción para la pregunta del accidente y cada fila representa una opción para la pregunta de DUI.
Las probabilidades marginales se pueden determinar a partir de la tabla de contingencia utilizando los valores totales externos para cada evento divididos por el tamaño total de la muestra.
- Probabilidad de que un conductor tuviera un accidente\(P(A)\) = = 100/1000 = 0.10
- Probabilidad de que un conductor no fue DUI\(P(D') = 1 ‐ P(D)\) = = 1 ‐ 200/1000 = 0.80
Las probabilidades conjuntas se pueden determinar a partir de la tabla de contingencia utilizando los valores internos de la tabla divididos por el tamaño total de la muestra.
- Probabilidad que un conductor tuvo un accidente y fue\(P(A \text{ and } D)\) DUI= = 70/1000 = 0.07
- Probabilidad que un conductor tuvo un accidente o fue\(P(A \text{ or } D)\) DUI= = (100+200‐70) /1000 = 0.23
Las probabilidades condicionales se pueden determinar a partir de la tabla de contingencia utilizando los valores internos de la tabla divididos por el valor total externo del evento condicional.
- Probabilidad de que un conductor fuera DUI dado que el conductor tuvo un accidente\(P(D|A)\) = = 70/100 = 0.70
- Probabilidad de que un conductor de DUI tuviera un accidente\(P(A|D)\) = = 70/200 = 0.35
Crear una tabla de dos a partir de probabilidades reportadas
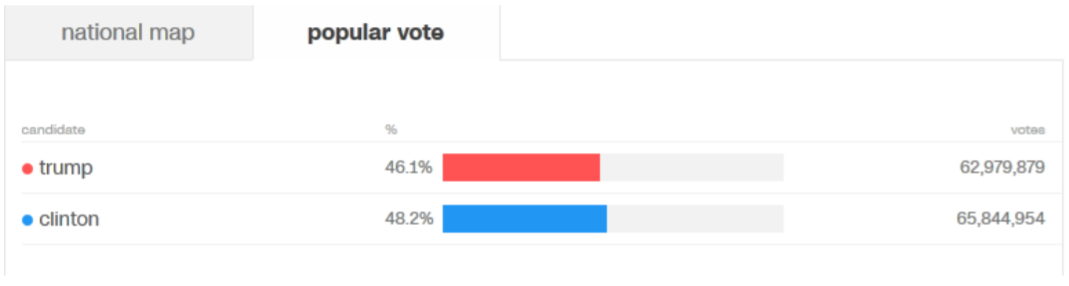
Podemos crear una hipotética tabla de dos vías a partir de probabilidades tabuladas cruzadas reportadas, como la encuesta de salida de CNN para las elecciones presidenciales de 2016:
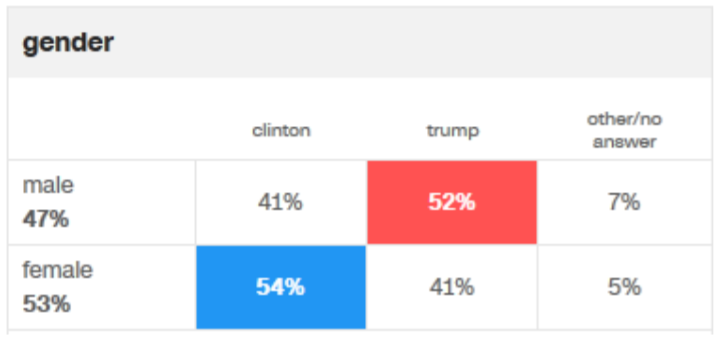
Paso 1: Elija un número total conveniente. (Esto se llama la base de la tabla).
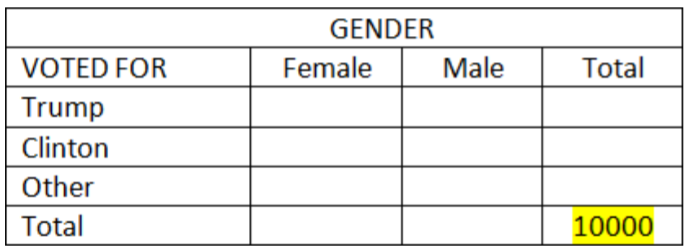
Radix elegido = 10000 votantes aleatorios
Paso 2: Determinar los valores externos de la tabla multiplicando la base por las probabilidades marginales para el género.
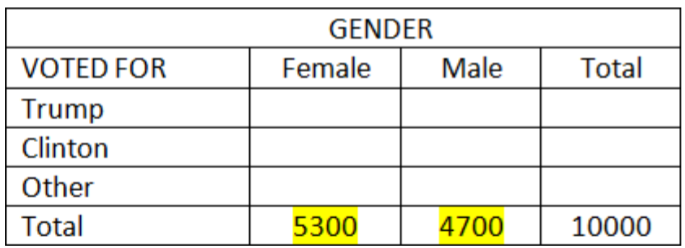
Total Mujeres = (0.53) (10000) = 5300
Total Hombres = (0.47) (10000) = 4700
Paso 3: Determinar los valores internos de la tabla multiplicando el total de género apropiado por las probabilidades condicionales de las encuestas de salida.
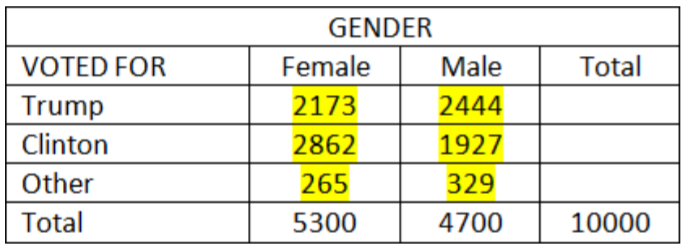
Trump Mujer = (0.41) (5300) = 2173
Clinton Mujer = (0.54) (5300) = 2862
Otras mujeres = (0.05) (5300) = 265
Trump Masculino = (0.52) (4700) = 2444
Clinton Hombre = (0.41) (4700) = 1927
Otro hombre = (0.057) (4700) = 329
Paso 4: Agrega cada fila para obtener los totales de fila.
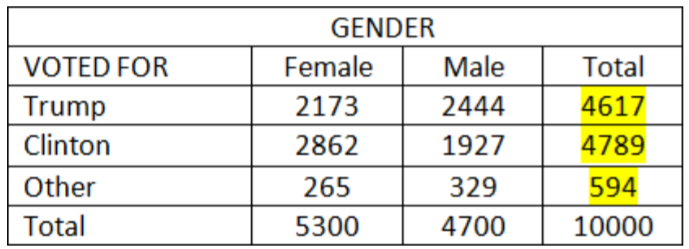
Trump = 2173 + 2444 = 4617
Clinton = 2862 + 1927 = 4789
Otro = 265 + 329 = 594
De la última columna, ahora podemos obtener las probabilidades marginales (que están ligeramente desviadas de la votación real debido al redondeo en las encuestas de salida): Donald Trump recibió 46%, Hillary Clinton recibió 48% y otros candidatos recibieron 6% del total de votos.