5.8: Diagramas multiplicativos de reglas y árboles
- Page ID
- 151863
Anteriormente, aprendimos sobre la regla aditiva para encontrar la probabilidad conjunta de la Unión de dos eventos. Existe una regla multiplicativa correspondiente para encontrar la probabilidad de la Intersección de dos eventos. Usando álgebra, esta regla puede calcularse directamente a partir de la Regla para Probabilidad Condicional.
Regla Multiplicativa de Probabilidad
\[P(A \text { and } B)=P(A) \times P(B \mid A) \nonumber \]
\[P(A \text { and } B)=P(B) \times P(A \mid B) \nonumber \]
Una manera útil de expresar la Regla Multiplicativa es mediante la creación de un diagrama de árbol, una forma sencilla de expresar todos los resultados posibles en una secuencia de eventos.
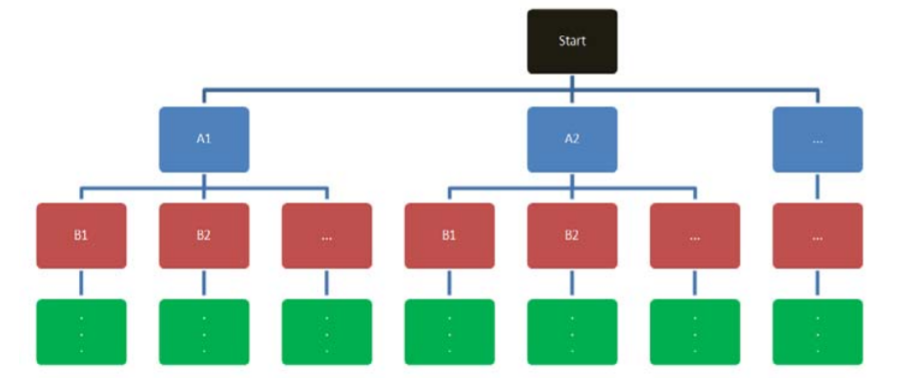
El primer nivel de ramas que se conectan al inicio son probabilidades marginales, y todos los niveles inferiores de ramas son probabilidades condicionales. Para encontrar la probabilidad de llegar al final de cualquier última rama, multiplique las probabilidades de todas las ramas que se conecten de nuevo a Inicio.
Ejemplo: Bolas rojas y verdes
Una caja contiene 4 bolas verdes y 3 bolas rojas. Se dibujan dos bolas, una a la vez, sin reemplazo. Haz un diagrama de árbol y encuentra la probabilidad de elegir dos bolas rojas.
Solución
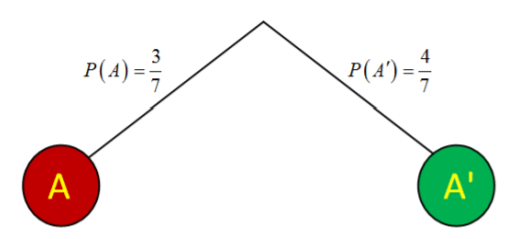
Que A sea el evento rojo en el primer Cuadro y B sea el evento R] rojo en el segundo sorteo. Entonces en este ejemplo A' sería el evento verde (no rojo) en el primero y B' sería el evento verde en el segundo sorteo.
Primero, hacer un árbol del primer sorteo y asignar probabilidades en función del número de bolas en la caja; 3 de 7 son rojas y 4 de 7 son verdes.
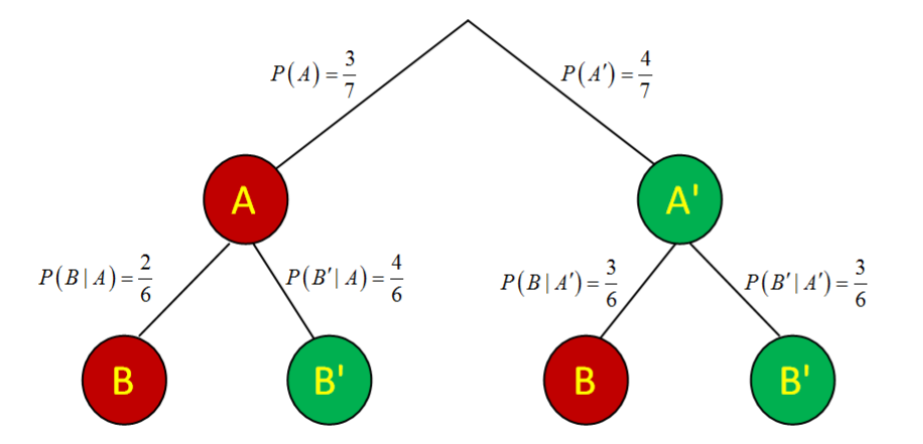
A continuación, realizar el segundo empate, asumiendo que el balón elegido en el primer empate se ha ido. Por ejemplo, si el primer empate fue rojo, la probabilidad de obtener otro rojo es de 2 de 6, ya que quedan 2 rojos y 4 verdes restantes. No obstante, si el primer empate fue verde, la probabilidad de ponerse rojo es de 3 sobre 6.
Por último, usa la regla multiplicativa y multiplica la rama para obtener todas las probabilidades conjuntas. Si ha construido el diagrama de árbol correctamente, todas estas probabilidades deben sumar a 1.
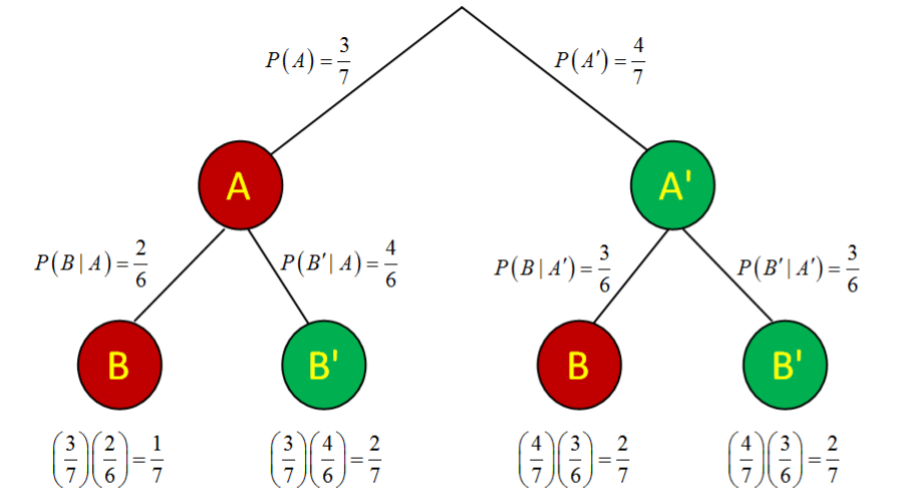
La probabilidad de obtener 2 bolas rojas es 1/7 o aproximadamente 0.143
Ejemplo: Interruptores de circuito
Un Circuito tiene tres interruptores lineales. Si al menos dos de los interruptores funcionan, el Circuito tendrá éxito. Cada switch tiene una tasa de fallas del 10% si todos están funcionando, y una tasa de fallas del 20% si un switch ya ha fallado. Construye un diagrama de árbol y encuentra la probabilidad de que el circuito tenga éxito.
Solución
Evento A = primer conmutador tiene éxito Evento A' = primer conmutador falla
Evento B = segundo conmutador tiene éxito Evento B' = segundo conmutador falla
Evento C = tercer conmutador tiene éxito Evento C' = tercer conmutador falla
P (2 o más éxitos) = 0.81 + 0.072 + 0.064 = 0.946
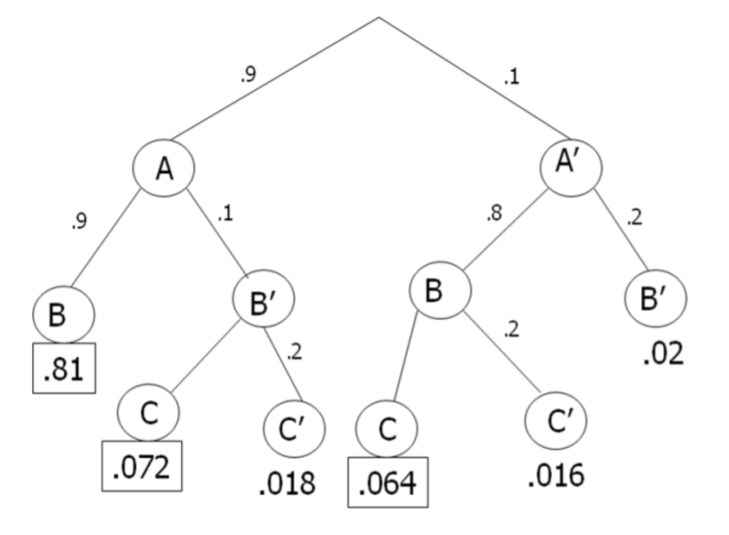
El switch tiene un 94.6% de posibilidades de éxito. Observe que no necesitábamos una tercera rama de desempate para los casos de los 2 primeros conmutadores que tuvieron éxito, o los primeros 2 interruptores fallaron.


