6.6: Distribución binomial
- Page ID
- 151528
La variable Aleatoria de Bernoulli ahora se puede extender a la Variable Aleatoria Binomial repitiendo el experimento un número fijo de veces. Es importante que cada uno de estos ensayos sea mutuamente independiente, lo que significa que el éxito o fracaso en un ensayo no cambia la probabilidad de éxito o fracaso en ensayos posteriores.
Por ejemplo, si volteas una moneda justa en la que las cabezas son iguales al éxito, entonces la probabilidad de éxito sería del 50% en cada prueba, independientemente de cuáles fueran los lanzamientos anteriores. Este es un ejemplo de independencia mutua, y la Distribución Binomial sería el modelo apropiado.
No obstante, si haces la pregunta “¿Llovió hoy?” , la probabilidad de que llueva al día siguiente probablemente sería mayor después de un día lluvioso. Este sería un ejemplo de no independencia mutua, y la Distribución Binomial no sería el modelo apropiado.
Ejemplo: Tiro libre
Volvamos al ejemplo de Draymond Green, un tirador de tiros libres del 70%. Ahora se lleva tres tiros libres y asumiremos que los éxitos en tiros libres son independientes. Let\(X\) = número de éxitos, que podría ser 0, 1, 2 o 3. Encuentra la media, probabilidad de varianza de que Draymond haga exactamente 2 tiros libres. En este ejemplo,\(n=3\) los ensayos y\(p=0.7\)
Solución
Debido a que la Distribución Binomial es una suma de ensayos independientes de Bernoulli, podemos simplemente multiplicar las fórmulas de Bernoulli por\(n\) para obtener media y varianza.
\(\mu=n p=(3)(0.7)=2.1\)
\(\sigma^{2}=n p(1-p)=(3)(.7)(.3)=0.63\)
Para encontrar la probabilidad de que Draymond Green haga tres tiros libres, podemos hacer un diagrama de árbol de todos los posibles resultados de Éxitos y Fracasos (S o F). Hay tres formas de hacer exactamente 2 tiros libres: SSF, SFS o FSS.
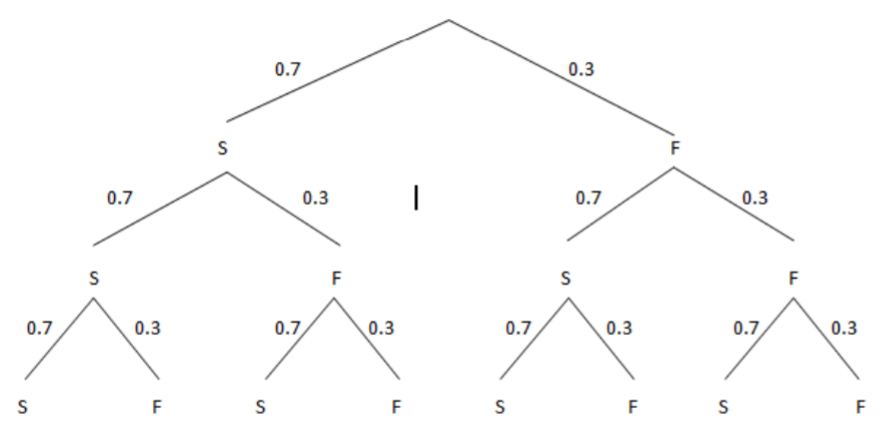
\(P(X=2)=P(S S F)+P(S F S)+P(F S S)=(3)(0.7)^{2}(0.3)^{1}=0.441\)
Hay alrededor de un 44% de posibilidades de que Draymond Green haga exactamente dos tiros libres en tres pruebas.
Para encontrar la probabilidad de que Draymond haga al menos 2 tiros libres, tendríamos que considerar también cuando haga los tres tiros (SSS).
\(P(X \geq 2)=P(X=2)+P(X=3)=(3)(0.7)^{2}(0.3)^{1}+(3)(0.7)^{3}(0.3)^{0}=0.441+.343=.784\)
Hay alrededor de un 78.4% de posibilidades de que Draymond Green haga al menos dos tiros libres en tres pruebas.
Para tamaños de muestra más grandes, los diagramas de árbol son demasiado tediosos de usar. Hay una fórmula para encontrar la probabilidad de exactamente x éxito en n ensayos:
\[P(x)={ }_{n} C_{x} p^{x}(1-p)^{n-x} \nonumber \]
La fórmula de combinación\({ }_{n} C_{x}=\dfrac{n !}{x !(n-x) !}\) significa el número de formas en que x éxitos pueden ocurrir de n ensayos. Esta fórmula también es tediosa de usar, por lo que confiaremos en tablas o tecnología para calcular las probabilidades binomiales.
Aquí un resumen de la Distribución Binomial
Distribución de probabilidad binomial (parámetros=\(n, p\))
\(n\)= número de ensayos independientes (tamaño de la muestra)
Dos posibles resultados (Éxito/Fracaso) o (Sí/No)
\(\mathbf{p} = P\)(sí/éxito) en un solo juicio
\(q = 1‐p = P\)(no/fracaso) en un solo juicio
\(X\)= Número de Sí/Éxitos {0, 1, 2,..., n}
\(\mu=n p\)
\(\sigma^{2}=n p(1-p)\)
\(\sigma=\sqrt{n p(1-p)}\)
\(P(x)={ }_{n} C_{x} p^{x}(1-p)^{n-x}\)
Ejemplo: Control de calidad
90% de las válvulas de globo súper dúplex 67 fabricadas son buenas (no defectuosas). Se selecciona una muestra de 10 válvulas. Definir la variable aleatoria y determinar los parámetros.

Solución
\(X\)= número de válvulas buenas en la muestra de 10.
\(n = 10, p = 0.9\)
Encuentra la media y varianza
\(\mu=n p=(10)(0.9)=9\)
\(\sigma^{2}=n p(1-p)=(10)(0.9)(0.1)=0.9\)
Para las siguientes preguntas de probabilidad, podemos usar tecnología o una tabla. La tabla mostrada fue creada por Minitab.

Encuentra la probabilidad de que se elijan exactamente 8 válvulas buenas.
\[P(X=8)=0.194 \nonumber \]
Encuentra la probabilidad de que se elijan 9 o más válvulas buenas.
\[P(X \geq 9)=P(9)+P(10)=0.387+0.349=0.736\nonumber \]
Encuentra la probabilidad de que se elijan 8 o menos válvulas buenas.
\[P(X \leq 9)=P(0)+P(1)+\ldots+P(8) \nonumber \]o en su lugar usar Regla de Complemento y ejemplo anterior
\[P(X \leq 9)=1-P(X \geq 9)=1-0.736=0.264 \nonumber \]


