7.3: Distribución Uniforme
- Page ID
- 151734
Una distribución uniforme es una variable aleatoria continua en la que todos los valores entre un valor mínimo y un valor máximo tienen la misma probabilidad.

Los dos parámetros que definen la Distribución Uniforme son:
\(a\)= mínimo\(b\) = máximo
La función de densidad de probabilidad es la función constante\(f(x) = 1/(b‐a)\), que crea una forma rectangular.
Ejemplo: Té de hojas sueltas
Un amante del té disfruta del té de hojas sueltas Tie Guan Yin y lo bebe frecuentemente. Para ahorrar dinero, cuando el suministro llegue a los 50 gramos comprará este popular té chino en un paquete de 1000 gramos.

La cantidad de té actualmente en stock sigue una variable aleatoria uniforme.
Solución
\(X\)= la cantidad de té actualmente en stock
\(a\)= mínimo = 50 gramos
\(b\)= máximo = 1050 gramos
\(f(x) = 1/(1050 ‐ 50) = 0.001\)

El valor esperado, la varianza poblacional y la desviación estándar se calculan utilizando las fórmulas:
\[\mu=\dfrac{a+b}{2} \qquad \sigma^{2}=\dfrac{(b-a)^{2}}{12} \qquad \sigma=\sqrt{\dfrac{(b-a)^{2}}{12}} \nonumber \]
Para el problema del té de hojas sueltas:
\(\mu=\dfrac{50+1050}{2}=550\)g
\(\sigma^{2}=\dfrac{(1050-50)^{2}}{12}=83,333\)
\(\sigma=\sqrt{83333}=289\)g
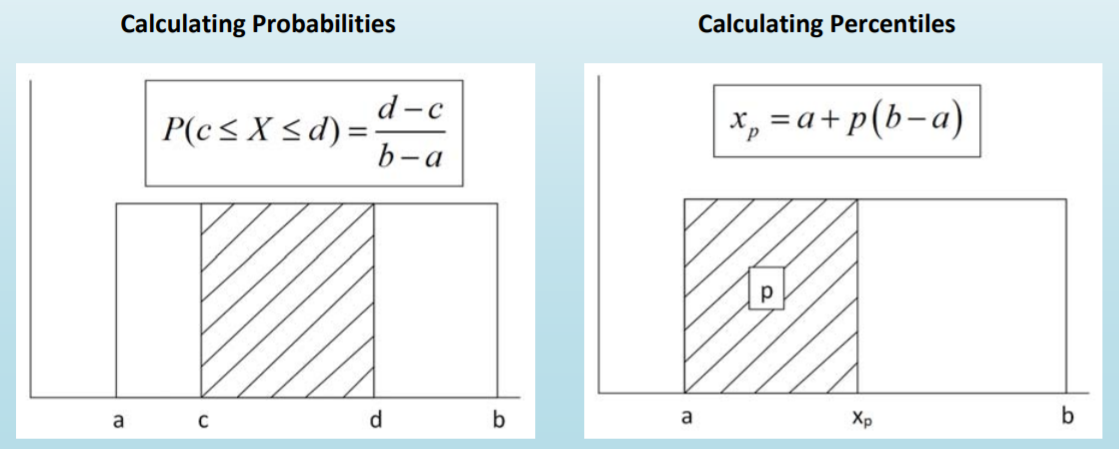
Los problemas de probabilidad pueden resolverse fácilmente encontrando el área de rectángulos.
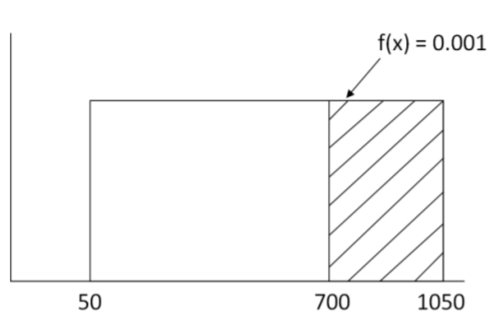
Encuentra la probabilidad de que haya al menos 700 gramos de té Tie Guan Yin en stock.
\(P(X \geq 700)=\text { width } \times \text { height }=(1050-700)(0.001)=0.35\)
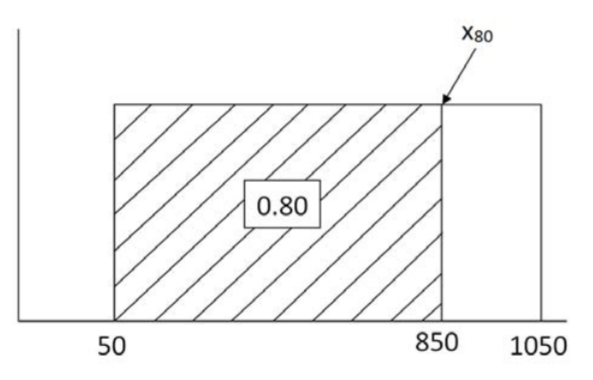
El\(p^{th}\) percentil de la Distribución Uniforme se calcula usando interpolación lineal:\(x_{p}=a+p(b-a)\)
Encuentra el\(80^{th}\) percentil de Tie Guan Yin en stock:
\(x_{80}=50+0.80(1050-50)=850\)gramos
Las características importantes de la Distribución Uniforme se resumen aquí:
Distribución Uniforme de Probabilidad (parámetros:\(a, b\))
\(a\)= valor mínimo
\(b\)= valor máximo
\(a \leq X \leq b\): Todos los valores de\(X\) entre\(a\) y\(b\) son igualmente probables
\(f(x)=\dfrac{1}{b-a}\)
\(\mu=\dfrac{a+b}{2}\)
\(\sigma^{2}=\dfrac{(b-a)^{2}}{12}\)
\(\sigma=\sqrt{\dfrac{(b-a)^{2}}{12}}\)
Ejemplo: Esperando un tren
El tren de cercanías Sounder 69 de Lakeview a Seattle, Washington llega a la estación de Tacoma cada 20 minutos durante la hora pico de la mañana. Supongamos que este tren está funcionando a tiempo.

- Encuentre el tiempo de espera esperado, desviación estándar, nad función de densidad de probabilidad para\(X\).
- Encuentra el Rango Intercuartílico para esta Variable Aleatoria. Primero encuentra los cuartiles\(1^{st}\) y ^ {rd}\).
- Encuentra la probabilidad de esperar al menos 15 minutos para el siguiente tren de cercanías después de llegar a la estación de Tacoma.
- Encuentra probabilidades condicionales para la Distribución Uniforme.
Solución
Let\(X\) = el tiempo de espera para que llegue el siguiente tren. X seguirá una Distribución Uniforme con el tiempo mínimo de espera de 0 minutos (solo toma el tren) y un tiempo máximo de espera de 20 minutos (simplemente pierde el tren).
- El tiempo de espera esperado es de 10 minutos:\(\mu=\dfrac{0+20}{2}=10\)
La desviación estándar es de 5.77 minutos:\(\sigma^{2}=\dfrac{(20-0)^{2}}{12}=33.33 \quad \sigma=\sqrt{33.33}=5.77\)
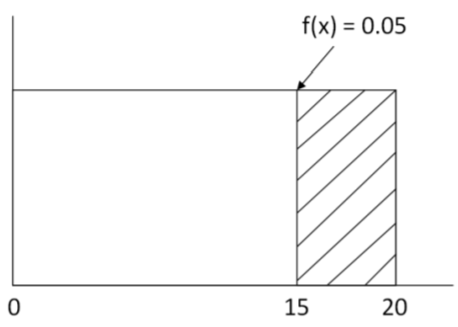
La función de densidad de probabilidad para X es:\(f(x)=\dfrac{1}{20-0}=0.05\)
- \ (\ begin {alineado}
&Q 1=x_ {25} =0+.25 (20-0) =5\\
&Q 3=x_ {75} =0+.75 (20-0) =15
\ end {alineado}\)
Intercuartil Rango =\(Q 3-Q 1=15-5=10\) minutos
- \(P(X \geq 15)=\dfrac{20-15}{20-0}=0.25\)
- Para encontrar probabilidades condicionales para la Distribución Uniforme, es más fácil simplemente crear una nueva Distribución Uniforme a partir de la información proporcionada.
Después de llegar a la estación de Tacoma, un commuter espera 5 minutos. Encuentra que la probabilidad de que el habitante vaya a esperar al menos 10 minutos adicionales (un total de 15 minutos) antes de que llegue el siguiente tren.
La declaración de probabilidad condicional se puede escribir como\(P(X \geq 15 \mid X \geq 5)\).
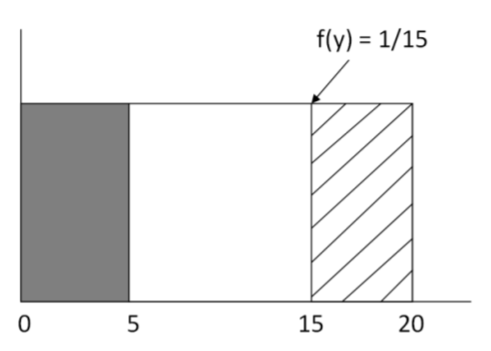
En su lugar, simplemente defina una nueva Variable Aleatoria\(Y\) = el tiempo de espera total esperado, asumiendo que el viajante espera al menos 5 minutos.
\(a\)= espera mínima = 5 minutos
\(b\)= espera máxima = 20 minutos
\(P(Y \geq 15)=\dfrac{20-15}{20-5}=0.333\)