8.2: Teorema del límite central para proporciones de muestra
- Page ID
- 151595
El Teorema del Límite Central también funcionará para proporciones de muestra si se cumplen ciertas condiciones.
La distribución binomial
En el Capítulo 6, exploramos la Variable Aleatoria Binomial, en la que\(X\) mide el número de éxitos en un número fijo de ensayos independientes. La distribución binomial tuvo dos parámetros: el tamaño\(n\) de la muestra y la probabilidad de éxito en un solo ensayo\(p\).
Ejemplo: Tiro libre
Recordemos el ejemplo de Draymond Green, un jugador de basquetbol de la NBA para los Golden State Warriors que es un tirador de tiros libres del 70%.
La variable aleatoria\(X\) = el número de éxitos cuando Draymond Green toma tiro\(n\) libre sigue a una Distribución de Bernoulli con\(p =0.7\) (éxito) y\(q = 0.3\) (fracaso). Vamos a graficar la función de distribución de probabilidad para\(n\) =1, 5, 25 y 100:
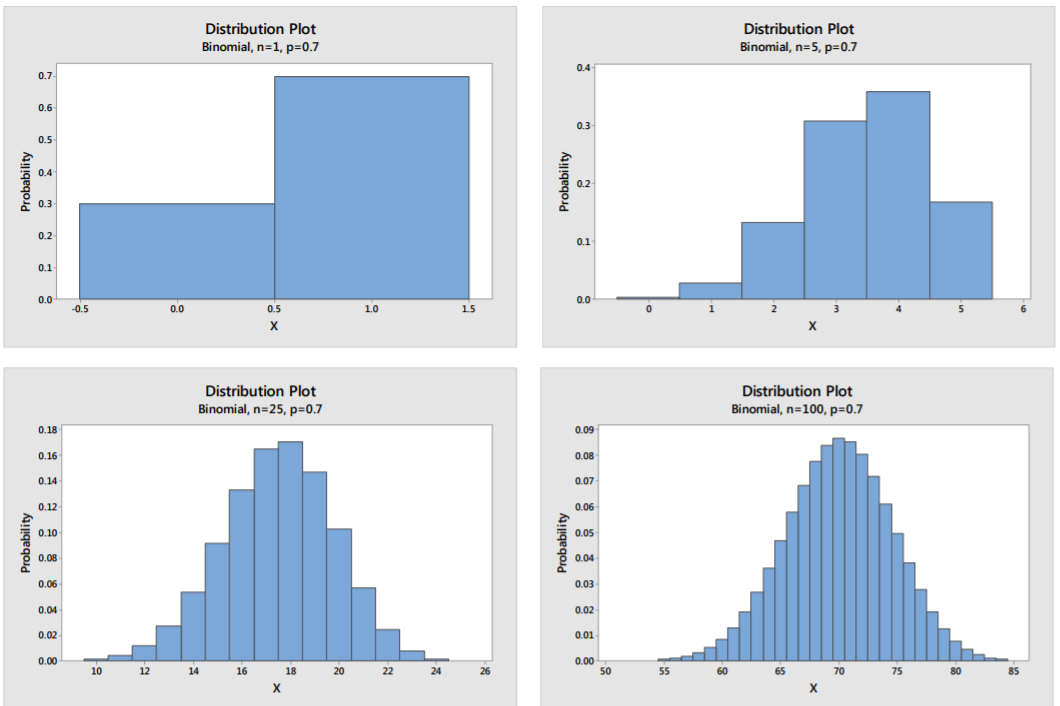
Observe que a medida que el tamaño de la muestra se hace más grande, la forma de la variable aleatoria se vuelve Normal.
Una buena regla para usar es que si\(np>10\) y\(n(1‐p) > 10\), la forma de la Distribución Binomial es aproximadamente Normal.
La variable aleatoria Proporción de muestra
En lugar de mirar el número de éxitos en un número fijo, considere la proporción de éxitos en estos ensayos. Utilizaremos el símbolo\(\hat{p}\) (leído como p‐hat) para representar la proporción de éxitos en los\(n\) ensayos. Si\(X\) es el número de éxitos en\(n\) ensayos,\(\hat{p}=\dfrac{X}{n}\) es la proporción muestral de éxitos en\(n\) ensayos.
Aquí hay una comparación de estas dos variables aleatorias:
| Variable aleatoria | \(X\) | \(\hat{p}\) |
|---|---|---|
| Valor esperado | \ (X\)” class="lt-estados-20900">\(\mu=n p\) | \ (\ hat {p}\)” class="lt-stats-20900">\(\mu_{\hat{p}}=p\) |
| Varianza | \ (X\)” class="lt-estados-20900">\(\sigma^{2}=n p(1-p)\) | \ (\ hat {p}\)” class="lt-stats-20900">\(\sigma_{\hat{p}}^{2}=\dfrac{p(1-p)}{n}\) |
| Desviación estándar | \ (X\)” class="lt-estados-20900">\(\sigma=\sqrt{n p(1-p)}\) | \ (\ hat {p}\)” class="lt-stats-20900">\(\sigma_{\hat{p}}=\sqrt{\dfrac{p(1-p)}{n}}\) |
Ejemplo: Tiro libre
Draymond Green, un tirador al 70% en tiros libres, se lleva 4 tiros libres.
\(X\)= El número de éxitos en 4 tiros libres.
\(\hat{p}=\dfrac{X}{n}\)= La proporción de éxitos en 4 tiros libres.
Determinar la función de distribución de probabilidad, el valor esperado y la desviación estándar para la variable aleatoria\(\hat{p}\).
Solución
| \(x\) | \(\hat{p}\) | \(P(\hat{p})\) |
|---|---|---|
| \ (x\)” class="lt-estados-20900">0 | \ (\ hat {p}\)” class="lt-stats-20900">0.00 | \ (P (\ hat {p})\)” class="lt-stats-20900">0.0081 |
| \ (x\)” class="lt-estados-20900">1 | \ (\ hat {p}\)” class="lt-stats-20900">0.25 | \ (P (\ hat {p})\)” class="lt-stats-20900">0.0756 |
| \ (x\)” class="lt-estados-20900">2 | \ (\ hat {p}\)” class="lt-stats-20900">0.50 | \ (P (\ hat {p})\)” class="lt-stats-20900">0.2646 |
| \ (x\)” class="lt-estados-20900">3 | \ (\ hat {p}\)” class="lt-stats-20900">0.75 | \ (P (\ hat {p})\)” class="lt-stats-20900">0.3087 |
| \ (x\)” class="lt-estados-20900">4 | \ (\ hat {p}\)” class="lt-stats-20900">1.00 | \ (P (\ hat {p})\)” class="lt-stats-20900">0.2401 |
\(\mu_{\hat{p}}=p=0.7\)
\(\sigma_{\hat{p}}=\sqrt{\dfrac{p(1-p)}{n}}=\sqrt{\dfrac{0.7(1-0.7)}{4}}=0.2291\)
El teorema del límite central para proporciones de muestra
Si\(X\) es una Variable Aleatoria de una Distribución Binomial con parámetros\(n\) y\(p\), y\(np > 10\) y\(n(1‐p) > 10\)
Entonces lo siguiente es cierto para la Proporción de Muestra\(\hat{p}=\dfrac{X}{n}\)
- \(\mu_{\hat{p}}=p\)
- \(\sigma_{\hat{p}}=\sqrt{\dfrac{p(1-p)}{n}}\)
- La Distribución de\(\hat{p}\) es aproximadamente Normal.
Combinando todo lo anterior en una sola fórmula:\(Z=\dfrac{\hat{p}-p}{\sqrt{\frac{p(1-p)}{n}}}\) donde\(Z\) representa la Distribución Normal Estándar.
Ejemplo: Exhibiciones de cuotas de California Community College
La gráfica a continuación muestra la inscripción en los Colegios Comunitarios de California y el porcentaje de estudiantes que están recibiendo Exhibiciones de Cuota de la Junta de Gobernadores (BOGFW) para ayudar económicamente. 70
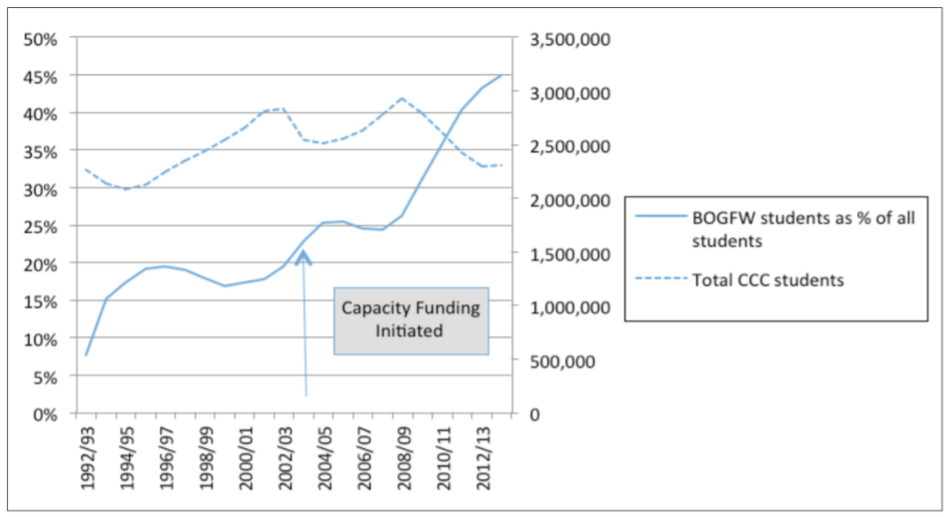
Esta gráfica muestra que 45% de todos los estudiantes de community college en California reciben exenciones de cuotas. Supongamos que muestrea aleatoriamente 1000 estudiantes de community college para determinar la proporción de estudiantes con exenciones de cuotas en la muestra.
\(p\)= 0.45 (la proporción de todos los estudiantes de colegios comunitarios con exenciones de cuotas)
\(n\)= 1000 (el tamaño de la muestra)
\(np = (1000)(0.45) = 450 n(1‐p) = (1000)(1‐0.45) = 550\).
Dado que ambos valores son superiores a 10, se cumplen las condiciones para la normalidad.
\(\hat{p}\)= la proporción de estudiantes de colegios comunitarios muestreados con exenciones de cuotas, una variable aleatoria
\(\mu_{\hat{p}}=0.45\)
\(\sigma_{\hat{p}}=\sqrt{\dfrac{0.45(1-.045)}{1000}}=0.0157\)
483 de los estudiantes muestreados están recibiendo exenciones de cuotas.
Determinar\(\hat{p}\). ¿El resultado es inusual?
Solución
\(\hat{p}=\frac{483}{1000}=0.483\)
\(Z=\frac{0.483-0.45}{0.0157}=2.10\)
\(P(Z>2.10)=0.0179\)
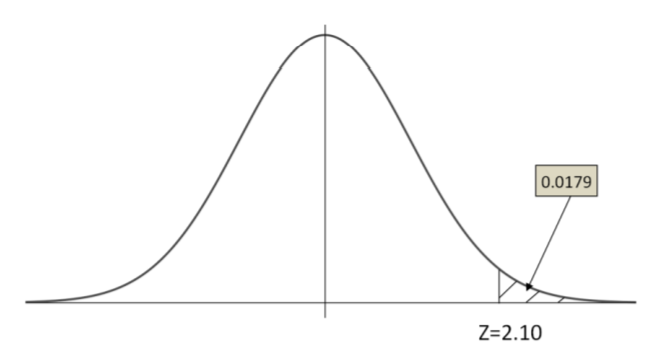
La proporción muestral de 0.483 es inusualmente alta, ya que el\(Z\) valor es superior a 2. La probabilidad de obtener una proporción muestral de 0.483 o mayor es de solo 0.0179.


