9.3: Intervalos de confianza
- Page ID
- 151463
Usando la probabilidad y el Teorema del Límite Central, podemos diseñar una Estimación de Intervalo llamada Intervalo de Confianza que tiene una probabilidad conocida (Nivel de Confianza) de capturar el parámetro de población real.
Intervalo de confianza para la media poblacional
Para encontrar un intervalo de confianza para la media poblacional (\(\mu\)) cuando se conoce la desviación estándar de la población (\(\sigma\)), y n es suficientemente grande, podemos usar la función de distribución de probabilidad de Distribución Normal Estándar para calcular los valores críticos para el Nivel de Confianza:

Ejemplo: Estudiantes trabajando
El Decano quiere estimar el número medio de horas que los estudiantes trabajaron por semana. Una muestra de 49 estudiantes mostró una media de 24 horas con una desviación estándar de 4 horas. La estimación puntual es de 24 horas (media muestral). ¿Cuál es el intervalo de confianza del 95% para el promedio de horas trabajadas por semana por los estudiantes?
Solución
\[24 \pm \dfrac{1.96 \cdot 4}{\sqrt{49}}=24 \pm 1.12=(22.88,25.12) \text{ hours per week} \nonumber \]
El margen de error para el intervalo de confianza es de 1.12 horas. Podemos decir con 95% de confianza que el número medio de horas trabajadas por los estudiantes está entre 22.88 y 25.12 horas semanales.
Si se incrementa el nivel de confianza, entonces también aumentará el margen de error. Por ejemplo, si aumentamos el nivel de confianza al 99% para el ejemplo anterior, entonces:
\[24 \pm \dfrac{2.578 \cdot 4}{\sqrt{49}}=24 \pm 1.47=(22.53,25.47) \text{ hours per week} \nonumber \]
Algunos puntos importantes sobre los intervalos de confianza
- El intervalo de confianza se construye a partir de variables aleatorias calculadas a partir de datos de muestra e intenta predecir un parámetro de población desconocido pero fijo con cierto nivel de confianza.
- Aumentar el nivel de confianza siempre aumentará el margen de error.
- Es imposible construir un Intervalo de Confianza del 100% sin realizar un censo de toda la población.
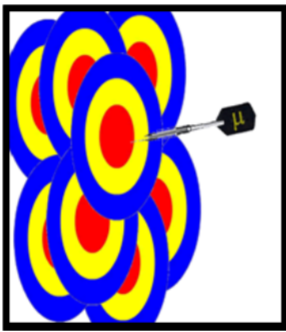
- Piense en la media poblacional como un dardo que siempre va al mismo punto, y el intervalo de confianza como un objetivo en movimiento que intenta “atrapar el dardo”. Un intervalo de confianza del 95% sería como un objetivo que tiene un 95% de probabilidad de atrapar el dardo.
Intervalo de confianza para la media poblacional usando la desviación estándar de la muestra — Distribución t de
La fórmula para el intervalo de confianza para la media requiere el conocimiento de la desviación estándar poblacional (\(\sigma\)). En la mayoría de los problemas de la vida real, desconocemos este valor por las mismas razones que desconocemos la media de la población. Este problema lo resolvió el estadístico irlandés William Sealy Gosset, empleado de Guinness Brewing. Gosset, sin embargo, fue prohibido por Guinness de usar su propio nombre en la publicación de artículos científicos. Publicó bajo el nombre de “A Student”, y por lo tanto la distribución que descubrió se denominó “Student\(t\) ‐distribution” 71.
Características de la distribución t de Student
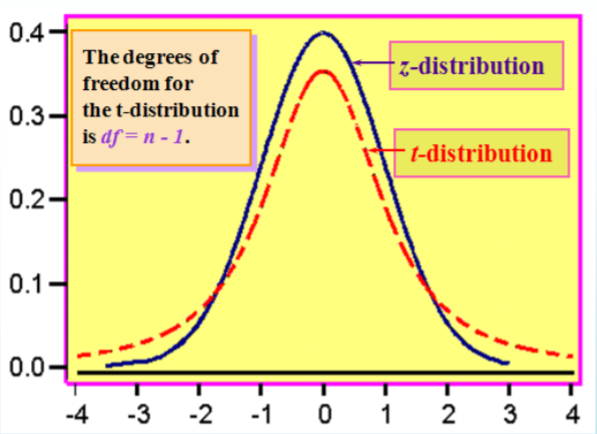
- Es continuo, en forma de campana y simétrico alrededor de cero como la\(z\) distribución.
- Existe una familia de\(t\) ‐distribuciones que comparten una media de cero pero que tienen diferentes desviaciones estándar basadas en grados de libertad.
- La\(t\) distribución ‐está más extendida y más plana en el centro que la\(Z\) distribución ‐, pero se acerca a la\(Z\) distribución a medida que el tamaño de la muestra aumenta.
Intervalo de confianza para\(\mu\)
\[\overline{X} \pm t_{c} \dfrac{s}{\sqrt{n}} \text{ with degrees of freedom} = n - 1 \nonumber \]
Ejemplo: Calificación de planes de salud
El año pasado Sally pertenecía a un plan de salud de la Organización de Mantenimiento de la Salud (HMO) que tenía una calificación promedio poblacional de 62 (en una escala de 0‐100, siendo '100' la mejor); esto se basó en registros acumulados sobre el HMO durante un largo periodo de tiempo. Este año Sally cambió a un nuevo HMO. Para evaluar la calificación media poblacional del nuevo HMO, se sondea a 20 miembros de este HMO y le dan a la HMO una calificación promedio de 65 con una desviación estándar de 10. Encontrar e interpretar un intervalo de confianza del 95% para la calificación promedio poblacional de la nueva HMO.
Solución
La\(t\) distribución tendrá 20‐1 =19 grados de libertad. Usando una tabla o tecnología, el valor crítico para el intervalo de confianza del 95% será\(t_c=2.093\)
\[65 \pm \dfrac{2.093 \cdot 10}{\sqrt{20}}=65 \pm 4.68=(60.32,69.68) \text{ HMO rating} \nonumber \]
Con 95% de confianza podemos decir que la calificación del nuevo HMO de Sally está entre 60.32 y 69.68. Dado que la cantidad 62 se encuentra en el intervalo de confianza, no podemos decir con 95% de certeza que el nuevo HMO sea mejor o peor que el HMO anterior.
Intervalo de confianza para la proporción de población
Recordemos de la sección sobre variables aleatorias la distribución binomial donde\(p\) representó la proporción de éxitos en la población. El modelo binomial era análogo al volteo de las monedas-o al sondeo de preguntas de sí/no. En la práctica, queremos utilizar estadísticas muestrales para estimar la proporción poblacional (\(p\)).
La proporción muestral (\(\hat{p}\)) es la proporción de éxitos en la muestra de tamaño\(n\) y es el estimador puntual para\(p\). Bajo el Teorema del Límite Central\(n(1-p)>10\), si\(n p>10\) y, la distribución de la proporción muestral\(\hat{p}\) tendrá una Distribución aproximadamente Normal.
Distribución normal para\(\hat{p}\) if Central Limit Theorem conditions are met.
\[\mu_{\hat{p}}=p \qquad \qquad \sigma_{\hat{p}}=\sqrt{\dfrac{p(1-p)}{n}} \nonumber \]
Con esta información podemos construir un intervalo de confianza para\(p\), la proporción poblacional:
Intervalo de confianza para\(p\)
\[\hat{p} \pm Z \sqrt{\dfrac{p(1-p)}{n}} \approx \hat{p} \pm Z \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \nonumber \]
Ejemplo: Hablar y conducir
200 conductores de California fueron muestreados al azar y se descubrió que 25 de estos conductores estaban hablando ilegalmente por sus celulares sin el uso de un dispositivo manos libres. Encuentra el estimador de puntos para la proporción de conductores que están usando sus celulares ilegalmente y construyen un intervalo de confianza del 99%.

Solución
El estimador de puntos para\(p\) es\(\hat{p}=\dfrac{25}{200}=.125\) o 12.5%.
Un intervalo de confianza del 99% para\(p\) es:\(0.125 \pm 2.576 \sqrt{\dfrac{.125(1-.125)}{200}}=.125 \pm .060\)
El margen de error para esta encuesta es del 6% y podemos decir con 99% de confianza que el verdadero porcentaje de conductores que están usando sus celulares ilegalmente está entre 6.5% y 18.5%
Estimador de puntos para la desviación estándar de la población
Muchas veces queremos estudiar la variabilidad, volatilidad o consistencia de una población. Por ejemplo, dos inversiones ambas tienen ganancias esperadas del 6% anual, pero una inversión es mucho más riesgosa, con mayores altibajos. Para estimar la variación o volatilidad de un conjunto de datos, utilizaremos la desviación estándar de la muestra\(s\) como estimador puntual de la desviación estándar poblacional (\(\sigma\)).
Ejemplo
Se sabe que las inversiones A y B tienen una tasa de rendimiento del 6% anual. Durante los últimos 24 meses, la Inversión A tiene una desviación estándar muestral de 3% al mes, mientras que la Inversión B tiene una desviación estándar muestral de 5% mensual. Diríamos que la Inversión B es más volátil y riesgosa que la Inversión A debido a la mayor estimación de la desviación estándar.
Para crear un intervalo de confianza para una estimación de la desviación estándar, necesitamos introducir una nueva distribución, llamada distribución Chi‐cuadrado (\(\chi^{2}\)).
La\(\chi^{2}\) distribución de Chi‐cuadrado
La distribución Chi‐cuadrado es una familia de distribuciones relacionadas con la Distribución Normal, ya que representa una suma de variables aleatorias normales estándar al cuadrado independientes. Al igual que la distribución t del Estudiante, los grados de libertad serán\(n - 1\) y determinarán la forma de la distribución. Además, dado que el Chi‐cuadrado representa datos cuadrados, la inferencia será sobre la varianza más que sobre la desviación estándar.
Características del Chi‐cuadrado\(\chi^{2}\) Distribution
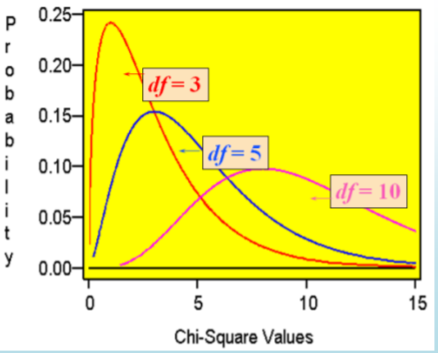
- Está sesgado positivamente
- No es negativo
- Se basa en grados de libertad (\(n - 1\))
- Cuando cambien los grados de libertad, se crea una nueva distribución que\(\dfrac{(n-1) s^{2}}{\sigma^{2}}\) tendrá distribución Chi‐cuadrada.
Intervalo de confianza para varianza poblacional y desviación estándar
Dado que el Chi‐cuadrado representa datos cuadrados, podemos construir intervalos de confianza para la varianza poblacional (\(\sigma^{2}\)), y tomar la raíz cuadrada de los puntos finales para obtener un intervalo de confianza para la desviación estándar de la población. Debido a la asimetría de la distribución Chi‐cuadrado, el intervalo de confianza resultante no se centrará en el estimador de puntos, por lo que el margen de error utilizado en los intervalos de confianza anteriores no tiene sentido aquí.
Intervalo de confianza para varianza poblacional (\(\sigma^{2}\))
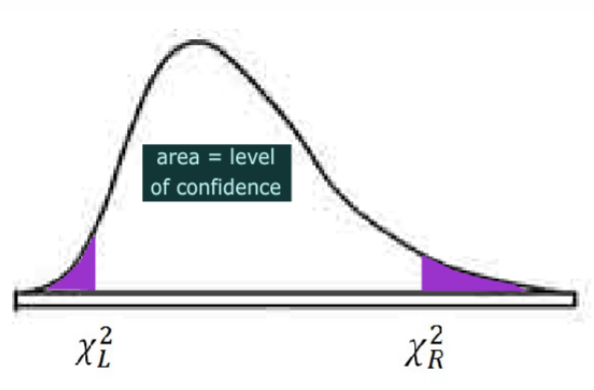
- La confianza NO es simétrica ya que la distribución chi‐cuadrada no es simétrica.
- Tomar raíz cuadrada de ambos puntos finales para obtener el intervalo de confianza para la desviación estándar de la población (\(\sigma\)).
\[\left(\dfrac{(n-1) s^{2}}{\chi_{R}^{2}}, \dfrac{(n-1) s^{2}}{\chi_{L}^{2}}\right) \nonumber \]
Ejemplo: Riesgo de desempeño en finanzas
En la medición del desempeño de las inversiones, la desviación estándar es una medida de volatilidad o riesgo. Veinte rendimientos mensuales de un fondo mutuo muestran un rendimiento mensual promedio de 1 por ciento y una desviación estándar muestral de 5 por ciento. Encontrar un intervalo de confianza del 95% para la desviación estándar mensual del fondo mutuo.

Solución
La distribución Chi‐cuadrada tendrá 20‐1 =19 grados de libertad. Usando la tecnología, encontramos que los dos valores críticos son\(\chi_{L}^{2}=8.90655\) y\(\chi_{R}^{2}=32.8523\)
La fórmula para el intervalo de confianza para\(\sigma\) es:\(\left(\sqrt{\dfrac{(19) 5^{2}}{32.8523}}, \sqrt{\dfrac{(19) 5^{2}}{8.90655}}\right)=(3.8,7.3)\)
Se puede decir con 95% de confianza que la desviación estándar para este fondo mutuo está entre 3.8 y 7.3 por ciento mensual.


