10.6: Prueba de Media vs Valor Hipotetizado — Un Ejemplo Completo
- Page ID
- 151735
Ejemplo — Producción de salsa de soja

Una empresa de alimentos tiene la política de que los contenidos declarados de un producto coinciden con los resultados reales. Una Pregunta General podría ser “¿El peso neto declarado de un producto alimenticio coincide con el peso real?” El estadístico de control de calidad decide probar la botella de 16 onzas de Salsa de Soja y ahora debe diseñar el experimento.
El estadístico de control de calidad ha sido autorizado para tomar muestras de 36 botellas de salsa de soja y sabe de pruebas anteriores que la desviación estándar de la población es de 0.5 onzas. El modelo será una prueba de media poblacional vs. valor hipotético de 16 oz Se selecciona una prueba de dos colas ya que a la compañía le preocupa tanto el sobrellenado como el llenado insuficiente de las botellas, ya que la política establecida es que el peso indicado debe coincidir con el peso real del producto.
Hipótesis de investigación:
\(H_o: \mu =16\)(La máquina de llenado funciona correctamente)
\(H_a: \mu \neq 16\)(La máquina de llenado no funciona correctamente)
Dado que se conoce la desviación estándar poblacional el estadístico de prueba será\(Z=\dfrac{\overline{X}-\mu}{\sigma / \sqrt{n}}\). Este modelo es apropiado ya que el tamaño muestral asegura que la distribución de la media muestral es aproximadamente Normal debido al Teorema del Límite Central.
El error tipo I sería rechazar la Hipótesis Nulo y decir que la máquina no está funcionando correctamente cuando de hecho estaba funcionando correctamente. Dado que la empresa no quiere detener innecesariamente la producción y recalibrar la máquina, el estadístico opta por limitar la probabilidad de error Tipo I estableciendo el nivel de significancia (\(\alpha\)) a 5%.
El estadístico ahora realiza el experimento y toma muestras de 36 botellas a lo largo de una hora y determina a partir de una gráfica de caja de los datos que hay una observación inusual de 17.56 onzas. El valor se vuelve a verificar y se mantiene en el conjunto de datos.
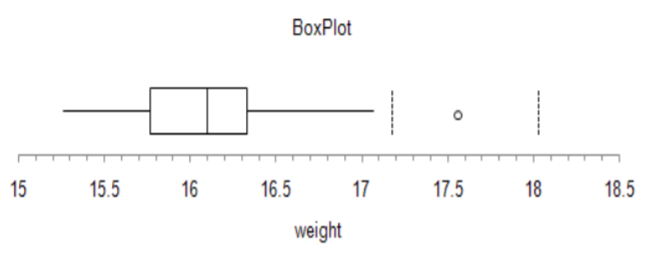
A continuación se calcula la media muestral y el estadístico de prueba.
\[\overline{X}=16.12 \text { ounces } \qquad \qquad Z=\dfrac{16.12-16}{0.5 / \sqrt{36}}=1.44 \nonumber \]
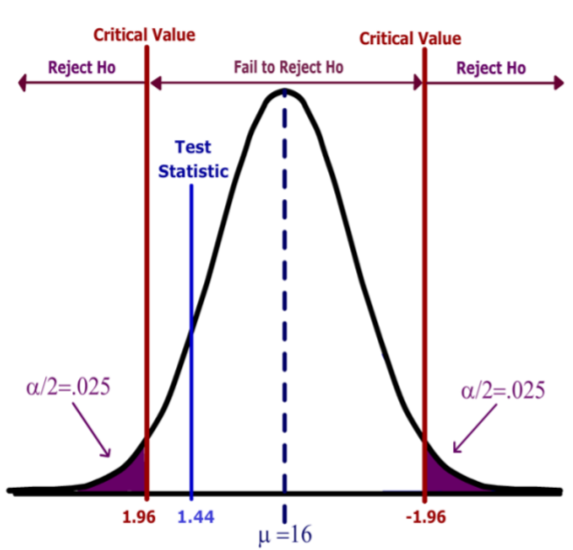
La regla de decisión bajo el método del valor crítico sería rechazar la Hipótesis Null cuando el valor del estadístico de prueba esté en la región de rechazo. Es decir, rechazar\(H_o\) cuando\(Z >1.96\) o\(Z<‐1.96\).
Con base en este resultado, la decisión es no rechazada\(H_o\), ya que el estadístico de prueba no cae en la región de rechazo.
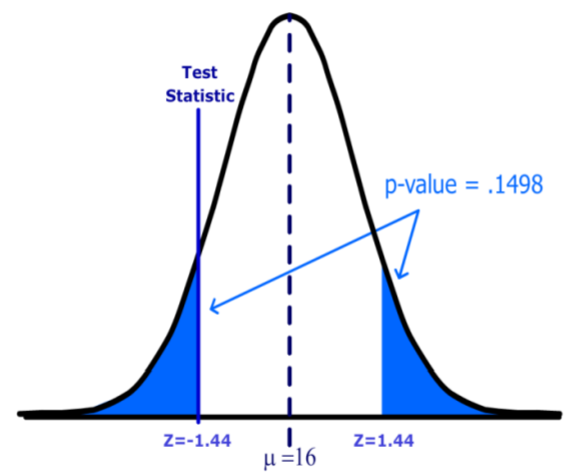
Alternativamente (y preferiblemente) el estadístico podría usar el método de la regla de decisión del valor p. El\(p\) ‐valor para una prueba de dos colas debe incluir todos los valores (positivos y negativos) más extremos que el estadístico de prueba, por lo que en este ejemplo encontramos la probabilidad de que\(Z < ‐1.44\) o\(Z > 1.44\) (el área sombreada en azul).
Usando una calculadora, software de computadora o una tabla Normal Estándar, el \(p\)‐valor=0.1498. Ya que el\(p\) ‐valor es mayor que\(\alpha\) la decisión de nuevo se deja de rechazar\(H_o\).
Por último, el estadístico deberá informar las conclusiones y hacer una recomendación a la dirección de la empresa:
“No hay pruebas suficientes para concluir que la máquina que llena botellas de salsa de soja de 16 onzas está funcionando incorrectamente. Esta conclusión se basa en 36 mediciones tomadas durante una sola hora de producción. Recomiendo seguir monitoreando la máquina durante diferentes turnos de empleados para dar cuenta de la posibilidad de un posible error humano”.
El estadístico hace la declaración débil y no está afirmando que la máquina esté funcionando correctamente, solo que no hay pruebas suficientes para afirmar que la máquina está funcionando incorrectamente. El estadístico también informa preocupaciones sobre el muestreo de un solo turno de empleados (restringiendo la inferencia a la población muestreada) y recomienda repetir el experimento en varios turnos.


