10.8: Nuevos modelos para la inferencia de una población, procedimientos similares
- Page ID
- 151737
Los procedimientos descritos para la prueba de media poblacional vs. valor hipotético con desviación estándar poblacional conocida también se aplicarán a otros modelos. Todo lo que realmente cambia es el estadístico de prueba.
Ejemplos de algunos otros modelos de una población:
- Prueba de media poblacional vs. valor hipotético, desviación estándar poblacional desconocida.
- Prueba de proporción poblacional vs. valor hipotético.
- Prueba de desviación estándar poblacional (o varianza) vs. valor hipotético.
Prueba de media poblacional con desviación estándar de población desconocida
El estadístico de prueba para el caso de una muestra cambia a una distribución t de Student con grados de libertad iguales a\(n-1: t=\dfrac{\overline{X}-\mu_{o}}{s / \sqrt{n}}\)
La forma de la\(t\) distribución es similar a la\(Z\), salvo por el hecho de que las colas son más gordas, por lo que la lógica de la regla de decisión es la misma que para el estadístico de\(Z\) prueba.
Ejemplo: Arqueología
Los huesos del húmero de la misma especie tienen aproximadamente las mismas proporciones de longitud a ancho. Cuando se descubren fósiles de huesos del húmero, los arqueólogos pueden determinar la especie examinando esta proporción. Se sabe que la Especie A tiene una relación media de 9.6. Una Especie B similar tiene una relación media de 9.1 y a menudo se confunde con la Especie A. 21 huesos de húmero fueron desenterrados en un área que originalmente se pensaba que era habitada Especie A. (Supongamos que todos los huesos desenterrados son de la misma especie.)
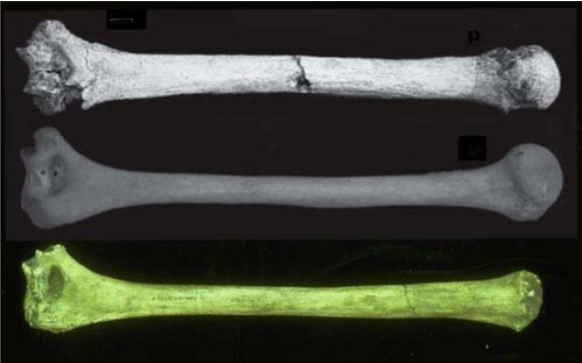
- Diseñar una prueba en la que la hipótesis alternativa sería que los huesos del húmero no fueran de la Especie A.
- Determinar el poder de esta prueba si los huesos provienen realmente de la Especie B (asumir una desviación estándar de 0.7)
- Realizar la prueba utilizando un nivel de significancia del 5% y exponer conclusiones generales.
Solución
- Hipótesis de investigación
\(H_o: \mu=9.6\)(Los huesos del húmero son de la Especie A)
\(H_a: \mu\neq9.6\)(Los huesos del húmero no son de la Especie A)
Nivel de significancia:\(\alpha\) =.05
Test Statistic (Modelo):\(t\) ‐test de media vs. valor hipotético, desviación estándar desconocida
Supuestos del modelo: es posible que necesitemos verificar la asimetría extrema en los datos, ya que se supone que la distribución de la media de la muestra es aproximadamente la Distribución Normal.
| Información necesaria para el cálculo de potencia | Resultados usando la calculadora de energía en línea 75 |
|---|---|
|
|
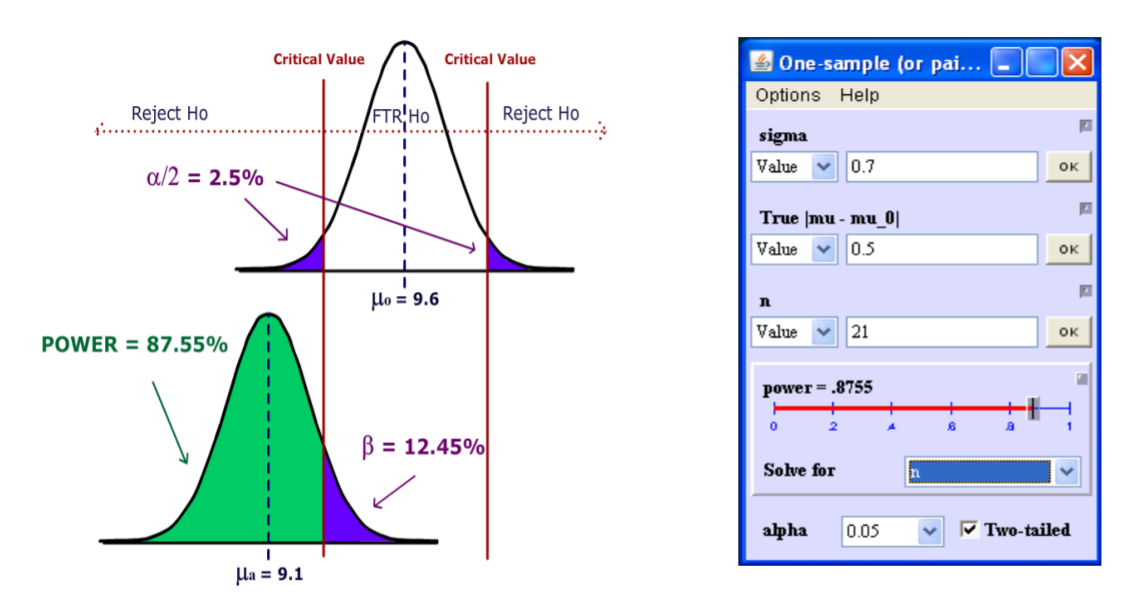
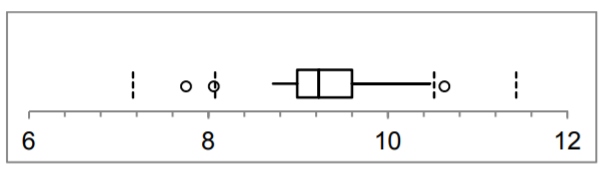
De MegaStat 76,\(p\) ‐valor = .0308 y\(\alpha\) =.05.
Ya que\(p\) ‐valor <\(\alpha\),\(H_o\) es rechazado y apoyamos\(H_a\).
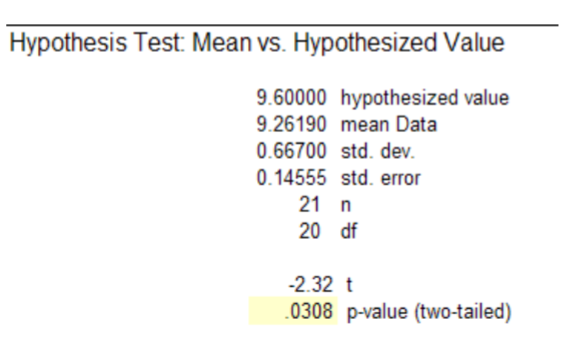
Conclusión: La evidencia apoya la afirmación (\(p\)‐valor < .05) de que los huesos del húmero no son de la Especie A. El pequeño tamaño de la muestra limitó la potencia de la prueba, lo que nos impidió hacer una conclusión más definitiva. Se recomiendan pruebas adicionales para determinar si los huesos son de la Especie B u otras especies desconocidas.
También estamos asumiendo que como los huesos fueron desenterrados en el mismo lugar, vinieron de la misma especie.
Prueba de proporción poblacional vs. valor hipotético
Cuando nuestros datos son categóricos y solo hay dos opciones posibles (por ejemplo, una pregunta de sí/no en una encuesta), es posible que queramos hacer una afirmación sobre una proporción o un porcentaje de la población (\(p\)) que se compara con un valor particular (\(p_o\)). Luego usaremos la proporción de muestra (\(\hat{p}\)) para probar el reclamo.
\(p\)= proporción poblacional
\(p_o\)= proporción poblacional\(H_o\)
\(\hat{p}\)= proporción muestral
\(p_a\)= proporción poblacional bajo Ha
Estadística de prueba:\(Z=\dfrac{\hat{p}-p_{o}}{\sqrt{\frac{p_{o}\left(1-p_{o}\right)}{n}}}\)
Requisito para la suposición de normalidad:\(n p(1-p)>5\)
Ejemplo: Solicitud de caridad
En el pasado, el 15% de las solicitudes de pedidos por correo para una determinada organización benéfica resultaron en una contribución financiera. Se ha redactado una nueva carta de solicitud que se enviará a una muestra aleatoria de posibles donantes. Se realizará una prueba de hipótesis para determinar si la nueva letra es más efectiva. Determinar la muestra para que (1) la prueba se ejecute al nivel de significancia del 5% y (2) si la letra tiene una tasa de éxito del 18%, (un tamaño de efecto del 3%), la potencia de la prueba será del 95%. Después de determinar el tamaño de la muestra, realizar la prueba.
Solución
\(H_o: p \leq 0.15\)(La nueva letra no es más efectiva.)
\(H_a: p > 0.15\)(La nueva letra es más efectiva.)
Test Statistic —\(Z\) ‐test de proporción vs. valor hipotético
| Información necesaria para el cálculo de potencia | Resultados usando la calculadora de energía en línea 75 |
|---|---|
|
|
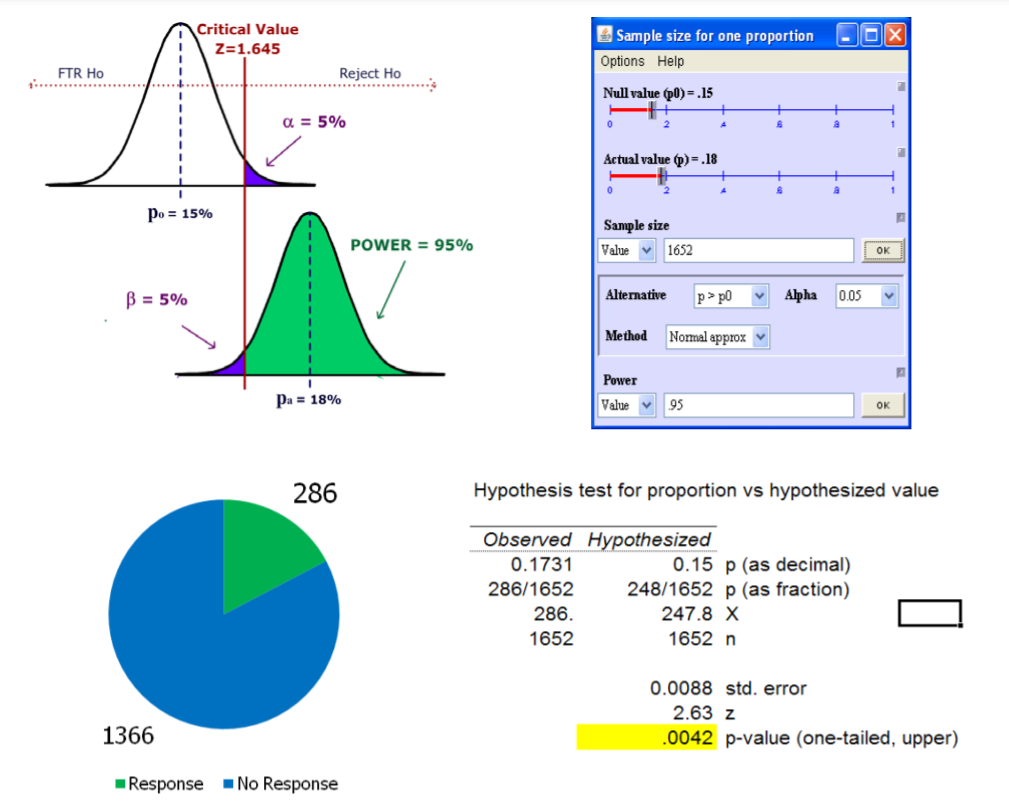
Desde\(p\) ‐valor <\(\alpha\), rechazo\(H_o\) y soporte\(H_a\). Dado que el\(p\) valor ‐es en realidad inferior a 0.01, iríamos más allá y diríamos que los datos admiten rechazar\(H_o\) for\(\alpha = .01\).
Conclusión: La evidencia sustenta la afirmación de que la nueva carta es más efectiva. Las 1652 cartas de prueba fueron seleccionadas como una muestra aleatoria de la lista de correo de la organización benéfica. Todas las cartas fueron enviadas en el mismo periodo de tiempo. Las cartas tenían que ser enviadas en un periodo de tiempo específico, por lo que no pudimos controlar por factores estacionales o económicos. Recomendamos probar ambos métodos de solicitación durante todo el año para eliminar los efectos estacionales y crear un grupo de control.
Prueba de desviación estándar poblacional (o varianza) vs. valor hipotético
A menudo queremos hacer una afirmación sobre la variabilidad, volatilidad o consistencia de una variable aleatoria poblacional. Los valores hipotéticos para la varianza poblacional (\(\sigma^{2}\)) o la desviación estándar (\(\sigma\)) se prueban con la distribución Chi‐cuadrado (\(\chi^{2}\)).
Ejemplos de Hipótesis:
- \(H_o: \sigma = 10 \)\(H_a: \sigma \neq 10\)
- \(H_o: \sigma^{2} = 100\)\(H_a: \sigma^{2} > 100\)
La varianza muestral\(s^2\) se utiliza para calcular el estadístico de prueba de Chi‐cuadrado.
\(\sigma^{2}\)= varianza poblacional
\(\sigma_{o}^{2}\)= varianza poblacional bajo Ho
\(s^2\)= varianza muestral
Estadística de prueba:\(\chi^{2}=\dfrac{(n-1) s^{2}}{\sigma_{o}^{2}}\)
\(n-1\)= grados de libertad
Ejemplo: Pruebas estandarizadas
Un administrador de escuelas estatales afirma que la desviación estándar de los puntajes de los exámenes para los estudiantes de octavo grado que tomaron una prueba de evaluación de ciencias de la vida es menor a 30, lo que significa que los resultados de la clase muestran consistencia. Un auditor quiere apoyar esa afirmación analizando los puntajes recientes de 41 estudiantes en las pruebas. La prueba se realizará a nivel de significancia del 1%.
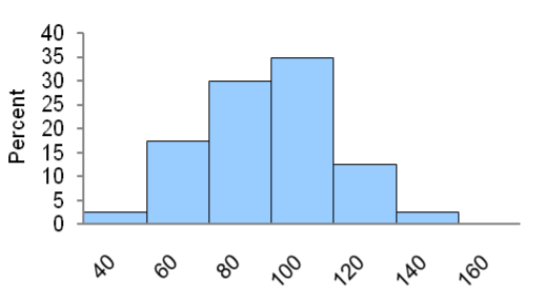
\ (\ begin {array} {|l|l|l|l|l|l|l|l|l|l|l|}
\ hline 57 y 75 y 86 y 92 y 101 y 108 y 110 y 120 y 155
\\ hline 63 y 77 y 88 y 96 y 102 y 108 y 111 y 122 y\\
\ hline 66 y 78 y 88 y 96 y 107 y 109 & 115 & 135 &\\
\ hline 68 & 81 & 92 & 98 & 107 & 109 & 115 & 137 &\\
\ hline 72 & 82 & 92 & 99 & 107 & 110 & 118 & 139 &\
\ hline
\ end {array}\)
Solución
Diseño:
Hipótesis de investigación:
\(H_o\): La desviación estándar para los resultados de las pruebas equivale a 30.
\(H_a\): La desviación estándar para los puntajes de las pruebas es menor a 30.
Hipótesis En cuanto a la varianza poblacional:
\(H_o: \sigma^{2} = 900\)
\(H_a: \sigma^{2} < 900\)
Resultados:
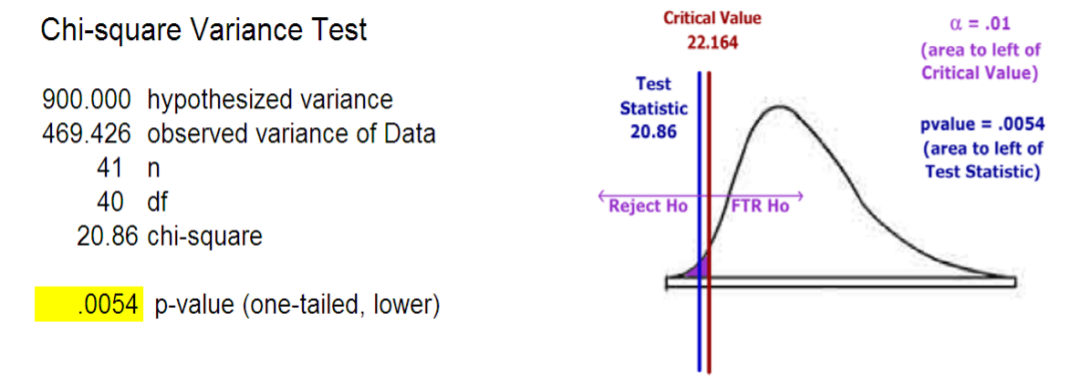
Decisión: Rechazar\(H_o\)
Conclusión: La evidencia respalda la afirmación (\(p\)‐valor < .01) de que la desviación estándar para los puntajes de las pruebas de octavo grado es menor a 30. Los 40 puntajes de las pruebas fueron los resultados del examen recientemente administrado a los estudiantes de octavo grado. Dado que los exámenes fueron solo para la clase actual, no hay garantía de que las clases futuras lograrán resultados similares. Otras investigaciones serían comparar resultados con otras escuelas que administraron el mismo examen y continuar analizando futuros exámenes de clase para ver si el reclamo se mantiene verdadero.


