11.3: Muestreo dependiente — Pares emparejados t‐test
- Page ID
- 151877
Los modelos independientes mostrados anteriormente compararon muestras que no estaban relacionadas. Sin embargo, a menudo es ventajoso tener muestras relacionadas que se emparejen, dos mediciones de una sola población. El modelo que consideraremos aquí se llama la \(t\)prueba de pares coincidentes, también conocida como\(t\) prueba de diferencia pareada. La ventaja de este diseño es que podemos eliminar la variabilidad porque no se están estudiando otros factores, aumentando la potencia del diseño.
En este modelo tomamos la diferencia de cada par y creamos una nueva población de diferencias, por lo que si efecto, la prueba de hipótesis es una prueba de una población de media que ya cubrimos en la sección anterior.
Pares
Supuestos de modelo
- Muestreo Dependiente
- \(X_{d}=X_{1}-X_{2}\)
- \(\overline{X}_{d}=\overline{X}_{1}-\overline{X}_{2}\)aproximadamente Normal
Estadística de prueba
- \(t=\dfrac{\overline{X}_{d}-\mu_{d}}{s_{d} / \sqrt{n}}\)
- \(d f=n-1\)
Ejemplo: Autos de renta
Una agencia de pruebas independiente está comparando el costo diario de alquiler de un auto compacto de Hertz y Avis.

Se obtiene una muestra aleatoria de 15 ciudades y se obtiene la siguiente información de renta.
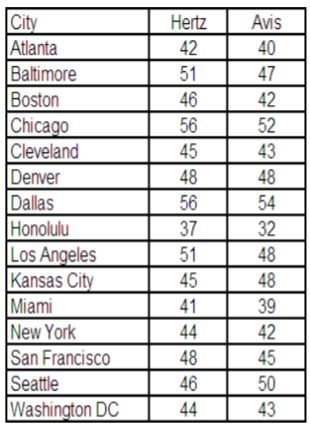
En el nivel de significancia .05 ¿puede la agencia de pruebas concluir que hay una diferencia en el alquiler cobrado?
Observe en este ejemplo que las ciudades son la población única que se está muestreando y que se están tomando dos medidas (Hertz y Avis) de cada ciudad. Usando el diseño de par emparejado, podemos eliminar la variabilidad debido a que las ciudades tienen un precio diferente (¡Honolulu es barato porque no puedes conducir muy lejos en Oahu!)
Solución
Diseño
Hipótesis de investigación:
\(H_o: \mu_{1}=\mu_{2}\)(Hertz y Avis tienen el mismo precio medio para los autos compactos).
\(H_a: \mu_{1} \neq \mu_{2}\)(Hertz y Avis no tienen el mismo precio medio para los autos compactos).
El modelo será emparejado par t‐test y estas hipótesis se pueden replantear como:\(Ho: \mu_{d}=0 \quad Ha: \mu_{d} \neq 0\)
La prueba se ejecutará a un nivel de significancia (\(\alpha\)) del 5%.
El modelo es de pares emparejados con dos colas\(t\), prueba con 14 grados de libertad. Rechazar\(H_o\) si\(t < ‐2.145\) o\(t >2.145\)
Datos/Resultados
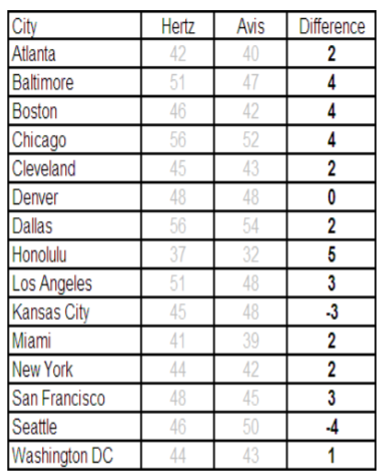
Tomamos la diferencia para cada par y encontramos la media de la muestra y la desviación estándar.
\ (\ begin {alineado}
\ overline {X} _ {d} &=1.80\\
s_ {d} & = 2.513\\
n &= 15\\
t&=\ dfrac {1.80-0} {2.513/\ sqrt {15}} =2.77
\ end {alineado}\)

Rechazar\(H_o\) bajo el método del valor crítico o del valor p.
Conclusión
Hay una diferencia en el precio medio de los autos compactos entre Hertz y Avis. Avis tiene precios medios más bajos.
La ventaja del diseño del par emparejado es clara en este ejemplo. La desviación estándar de la muestra para los precios de Hertz es de $5.23 y para Avis es de $5.62. Gran parte de esta variabilidad se debe a las ciudades, y el diseño de pares emparejados reduce drásticamente la desviación estándar a $2.51, lo que significa que la prueba t de pares emparejados tiene significativamente más potencia en este ejemplo.


