15.2.5: Capítulo 6 Tarea
- Page ID
- 151439
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
- Explicar la diferencia entre los parámetros poblacionales y los estadísticos muestrales. ¿Qué símbolos utilizamos para la media y la desviación estándar para cada uno de estos?
- Considere la siguiente función de distribución de probabilidad de la variable aleatoria X, que representa el número de personas en un grupo (fiesta) en un restaurante:
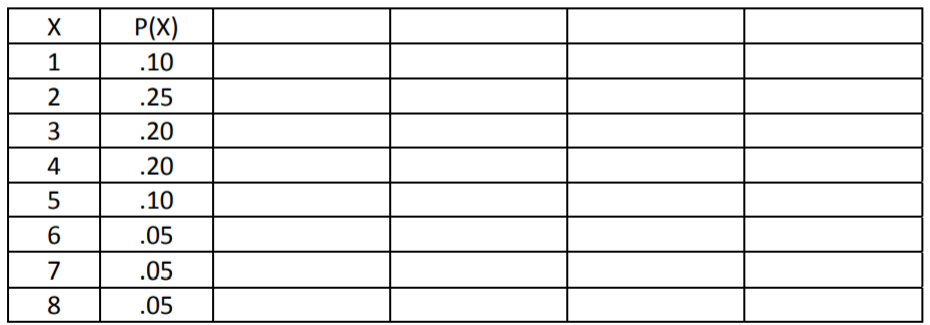
- Encuentra la media poblacional de X.
- Encuentra la varianza poblacional y desviación estándar de X.
- Encuentra la probabilidad de que la próxima fiesta sea mayor de 4 personas.
- Encuentra la probabilidad de que los siguientes tres partidos (asumiendo la independencia) sean cada uno de más de 4 personas.
- El 10% de todos los niños de un gran distrito escolar urbano de primaria han sido diagnosticados con discapacidades de aprendizaje. 10 niños son seleccionados al azar e independientemente de este distrito escolar.
- Dejar X = el número de niños con discapacidades de aprendizaje en la muestra. ¿Qué tipo de variable aleatoria es esta?
- Encuentra la media y desviación estándar de X.
- Encuentra la probabilidad de que exactamente 2 de estos niños seleccionados tengan una discapacidad de aprendizaje.
- Encuentra la probabilidad de que al menos 1 de estos niños tenga una discapacidad de aprendizaje.
- Encuentra la probabilidad de que menos de 3 de estos niños tengan una discapacidad de aprendizaje.
- Se hace una declaración general de que se produce un error en el 10% de todas las transacciones minoristas. Deseamos evaluar la veracidad de esta cifra para una tienda minorista en particular, digamos tienda A. Veinte transacciones de esta tienda se obtienen aleatoriamente. Suponiendo que la cifra del 10% también se aplica a la tienda A, y deja que X sea el número de transacciones minoristas con errores en la muestra
- La función de distribución de probabilidad (pdf) de X es binomial. Identificar los parámetros n y p.
- Calcular el valor esperado de X.
- Calcular la varianza de X.
- Encuentra la probabilidad exactamente 2 transacciones muestreadas están en error.
- Encuentra la probabilidad de que al menos 2 transacciones muestreadas estén en error.
- Encuentra la probabilidad de que no haya más de una transacción en error.
- ¿Sería inusual que 5 o más transacciones estuvieran en error?
- Un periódico encuentra una media de 4 errores tipográficos por página. Supongamos que los errores siguen una distribución de Poisson.
- Sea X igual al número de errores en una página. Encuentra la media y desviación estándar de esta variable aleatoria.
- Encuentra la probabilidad de que se encuentren exactamente tres errores en una página.
- Encuentra la probabilidad de que no se encuentren más de 2 errores en una página.
- Encuentra la probabilidad de que no se encuentren más de 2 errores en dos páginas.
- Los accidentes mayores en una refinería regional ocurren en promedio una vez cada cinco años. Supongamos que los accidentes siguen una distribución de Poisson.
- ¿Cuántos accidentes esperarías a lo largo de 10 años?
- Encuentra la probabilidad de que no haya accidentes en los próximos 10 años.
- Encuentra la probabilidad de que no haya accidentes en los próximos 20 años.
- El 20% de la gente de un pueblo de California se considera vegetariana. Si 20 personas son muestreadas aleatoriamente, encuentre la probabilidad de que:
- Exactamente 3 son vegetarianos.
- Al menos 3 son vegetarianos.
- A lo sumo 3 son vegetarianos
- El 20% de la gente de un pueblo de California se considera vegetariana. Las personas son muestreadas hasta que se encuentra el primer vegetariano. Utilice la distribución geométrica para encontrar las siguientes probabilidades:
- Se recoge a un vegetariano en el primer juicio.
- Un vegetariano se recoge en algún lugar dentro de las tres primeras pruebas.
- Un vegetariano no se recoge hasta algún momento después del tercer juicio.
- Los buques de carga llegan a un muelle de carga a razón de 2 por día. El muelle tiene la capacidad de manejar 3 llegadas por día. ¿Cuántos días al mes (suponga 30 días en un mes) esperarías que el muelle no pueda manejar todos los barcos que llegan? (Pista: primero encuentra la probabilidad de que lleguen más de 3 barcos, y luego use esa probabilidad para encontrar el número esperado de días en un mes que lleguen demasiados barcos).
- Grandes huracanes golpean la costa de Estados Unidos a una tasa de 0.7 por año.
- ¿Cuál es la probabilidad de que 4 huracanes importantes azoten la costa de Estados Unidos en un año?
- ¿Cuál es la probabilidad de que más de 2 huracanes importantes azoten la costa de Estados Unidos en 2 años?
- ¿Cuál es la probabilidad de que ningún huracán importante golpee la costa de Estados Unidos en los próximos 5 años?
- En 2017, 3 huracanes importantes tocaron tierra en Estados Unidos, causando daños catastróficos a Texas, Florida, Puerto Rico y las Islas Vírgenes. Encuentra la probabilidad de que tres grandes huracanes toquen tierra en un año.


