15.2.6: Capítulo 7 Tareas
- Page ID
- 151453
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
- El tiempo de finalización (en minutos) para que un estudiante complete un breve cuestionario sigue la función de densidad de probabilidad que se muestra aquí, con algunas áreas calculadas.
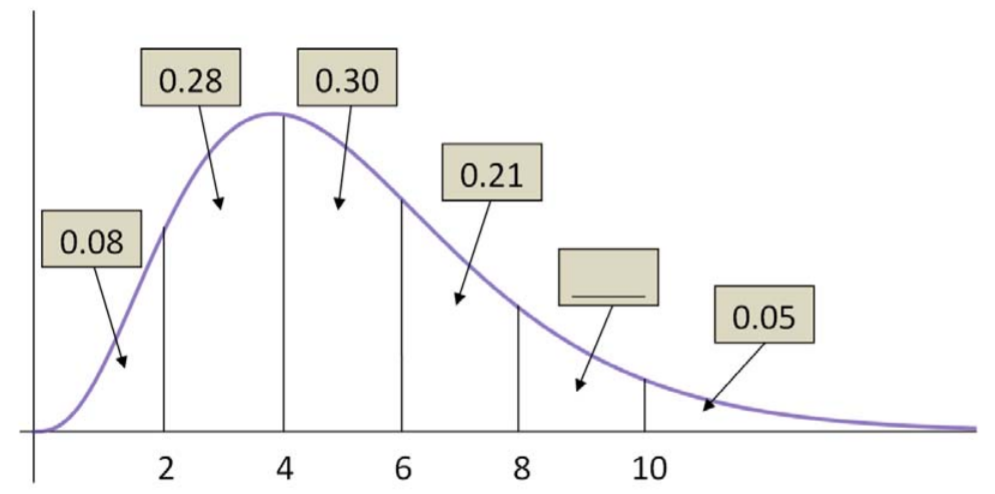
- Encuentra la probabilidad de que un alumno complete el examen en 4 minutos o menos.
- Encuentra la probabilidad de que un estudiante necesite entre 8 y 10 minutos para terminar el cuestionario.
- Si el instructor permite 10 minutos para el cuestionario y la clase tiene 40 alumnos, ¿a cuántos estudiantes se les quedará sin tiempo antes de que termine el cuestionario?
- Encuentra el percentil 64 de la distribución.
- Un ferry sale del muelle una vez por hora. Su tiempo de espera para el próximo ferry seguirá una distribución uniforme de 0 a 60 minutos.
- Encuentra la media y varianza de esta variable aleatoria.
- Encuentra la probabilidad de esperar más de 20 minutos para el próximo ferry.
- Encuentra la probabilidad de esperar exactamente 20 minutos para el próximo ferry.
- Encuentra la probabilidad de esperar entre 15 y 35 minutos para el próximo ferry.
- Encuentra la probabilidad condicional de esperar al menos 10 minutos más después de haber esperado ya 15 minutos.
- Encuentra la probabilidad de esperar más de 45 minutos para el ferry en 3 días consecutivos independientes.
- Los tiempos de ciclo de un camión que transportan concreto a un sitio de construcción de carreteras se distribuyen uniformemente en el intervalo de 50 a 70 minutos.
- Encuentra la media y varianza para los tiempos de ciclo.
- Encuentra el percentil 5 y 95 de los tiempos de ciclo.
- Encuentra la gama intercuartil.
- Encuentra la probabilidad de que el tiempo de ciclo de un camión seleccionado aleatoriamente supere los 62 minutos.
- Si se le da que el tiempo de ciclo supera los 55 minutos, encuentre la probabilidad de que el tiempo de ciclo esté entre 60 y 65 minutos.
- La cantidad de gasolina en el tanque de un automóvil (X) sigue una Distribución Uniforme, en la que el mínimo es cero y el máximo es de 12 galones.
- Encuentra la cantidad media y mediana de gas en el tanque.
- Encuentra la varianza y desviación estándar del gas en el tanque.
- Encuentra la probabilidad de que haya más de 3 galones en el tanque.
- Encuentra la probabilidad de que haya entre 4 y 6 galones en el tanque.
- Encuentra la probabilidad de que haya exactamente 3 galones en el tanque.
- Encuentra el percentil 80 de gas en el tanque.
- Una población normalmente distribuida de pesos de paquete tiene una media de 63.5 g y una desviación estándar de 12.2 g.
- ¿Qué porcentaje de esta población pesa 66 g o más?
- ¿Qué porcentaje de esta población pesa 41 g o menos?
- ¿Qué porcentaje de esta población pesa entre 41 g y 66 g?
- Encuentra el percentil 60 para la distribución de pesos.
- Encuentra los tres cuartiles y la gama intercuartil.
- Asumir el tiempo de espera esperado hasta el próximo terremoto RM (Richter Magnitud) 7.0 o mayor en algún lugar de California siga una distribución exponencial con\(\mu=10\) años.
- Encuentra la probabilidad de esperar 10 o más años para el próximo terremoto RM 7.0 o mayor.
- Determinar la mediana del tiempo de espera hasta el próximo terremoto RM 7.0 o mayor.
- El Jarabe de Maíz Alto en Fructosa (HFCS) es un edulcorante en productos alimenticios que está relacionado con la obesidad y la Diabetes Tipo 2. El consumo medio anual en Estados Unidos en 2008 de HFCS fue de 60 lbs con una desviación estándar de 20 lbs. Supongamos que la población sigue una Distribución Normal.
- Encuentre la probabilidad de que un estadounidense seleccionado al azar consuma más de 50 lbs de HFCS por año.
- Encuentre la probabilidad de que un estadounidense seleccionado al azar consuma entre 30 y 90 lbs de HFCS por año.
- Encuentra el percentil 80 del consumo anual de HFCS.
- ¿Entre qué dos números esperarías que contengan 95% del consumo anual de HFCS de los estadounidenses?
- Encuentra los cuartiles y el rango intercuartílico para esta población.
- Un adolescente al que le encantan los refrescos consume 105 lbs de HFCS al año. ¿Este resultado es inusual? Usa la probabilidad para justificar tu respuesta.
- Una central nuclear experimenta accidentes graves una vez cada 8 años. Dejar X = el tiempo de espera hasta el próximo accidente grave.
- ¿Cuál es la media y la desviación estándar de la variable aleatoria X?
- Determinar la probabilidad de esperar más de 10 años antes del próximo accidente grave.
- Supongamos que una planta pasó 5 años sin un accidente grave. Encuentra la probabilidad de esperar más de 10 años antes del próximo accidente grave.
- Determinar la probabilidad de esperar menos de 5 años antes del siguiente accidente grave.
- ¿Cuál es el tiempo medio de espera hasta el próximo accidente grave?
- Encuentra la gama Intercuartil para esta distribución.


