15.2.7: Capítulo 8 Tarea
- Page ID
- 151426
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
- Indique en sus propias palabras las 3 partes importantes del Teorema del Límite Central.
- Para las mujeres de 18 a 24 años, las presiones arteriales sistólicas (en mmHg) se distribuyen normalmente con\(\mu=114.8\) y\(\sigma=13.1\)
- Encuentra la probabilidad de que una mujer de 18 a 24 años tenga una presión arterial sistólica superior a 120.
- Si se seleccionan al azar a 4 mujeres, encuentra la probabilidad de que su presión arterial media supere 120.
- Si 40 mujeres son seleccionadas al azar, encuentra la probabilidad de que su presión arterial media supere 120.
- Si el pdf para la presión arterial sistólica NO siguió una distribución normal, ¿cambiaría su respuesta a la parte c? Explique.
- Una población normalmente distribuida de pesos de paquete tiene una media de 63.5 g y una desviación estándar de 12.2 g.
- Si muestrea 1 paquete, encuentra la probabilidad de que la media de la muestra sea superior a 66 g.
- Si toma una muestra de 16 paquetes, encuentre la probabilidad de que la media de la muestra sea superior a 66 g. Compare esta respuesta con la parte a.
- Si toma muestras 49 paquetes, encuentre la probabilidad de que la media de la muestra sea superior a 66 g. Compare esta respuesta con las partes a y b.
- El Jarabe de Maíz Alto en Fructosa (HFCS) es un edulcorante en productos alimenticios que está relacionado con la obesidad y la Diabetes Tipo 2. El consumo medio anual en Estados Unidos en 2008 de HFCS fue de 60 lbs con una desviación estándar de 20 lbs. Supongamos que la población sigue una Distribución Normal.
- En una muestra de 16 estadounidenses, ¿cuál es la probabilidad de que la media de la muestra supere las 57 libras de HFCS al año?
- En una muestra de 16 estadounidenses, cuál es la probabilidad de que la media de la muestra esté entre 50 y 70 libras de HFCS al año.
- En una muestra de 16 estadounidenses, ¿entre qué dos valores esperarías ver 95% de las medias de la muestra?
- El tiempo de finalización (en minutos) para que un estudiante complete un cuestionario breve sigue la función de densidad de probabilidad continua que se muestra aquí, con algunas áreas calculadas. Se sabe que\(\mu=5.3\) minutos y\(\sigma=2.4\) minutos. 40 alumnos toman el cuestionario.
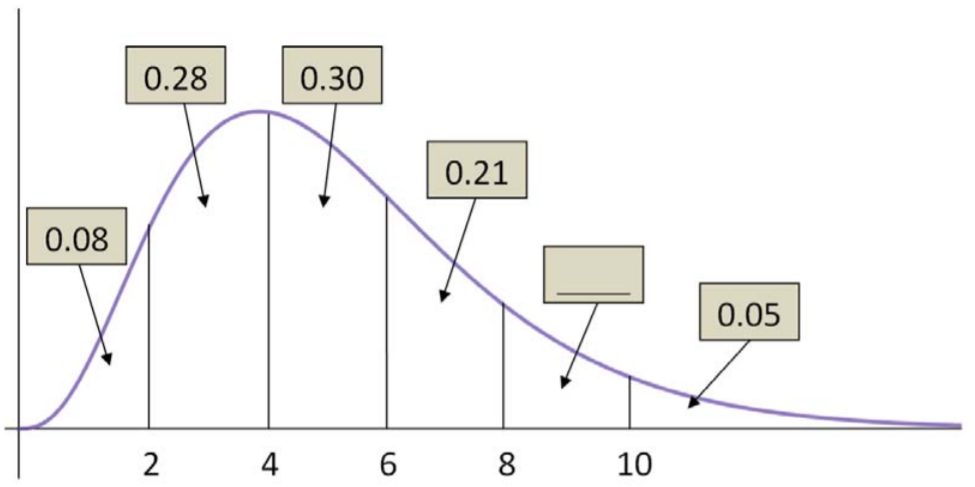
- Encontrar el tiempo medio de finalización para los estudiantes es menor de 5 minutos.
- Encuentra la probabilidad de que el tiempo medio para que la clase termine el cuestionario sea entre 6 y 8 minutos.
- El tiempo medio de finalización para la clase fue de 7.1 minutos. ¿Este resultado es inusual? Explique.
- Un encuestador tomó muestras de 100 adultos en California e hizo una serie de preguntas. El Teorema del Límite Central para Proporciones requiere que\(np > 10\) y\(n(1‐p) > 10\). Determinar si se cumplen estas condiciones para las siguientes declaraciones.
- El 61% de los californianos vive en el sur de California.
- 92% de los californianos apoyan Acción Diferida para los Llegados en la Infancia (DACA).
- El 24% de los californianos han visitado el Parque Nacional Yosemite.
- 8% de los californianos tienen una condena por delito grave.
- Los tiempos de ciclo de un camión que transporta concreto a un sitio de construcción de carreteras se distribuyen uniformemente en el intervalo de 50 a 70 minutos. Para la Distribución Uniforme\(\mu=\dfrac{a+b}{2}\) y\(\sigma=\sqrt{\dfrac{(b-a)^{2}}{12}}\), en la que\(a\) está el valor mínimo y\(b\) es el valor máximo.
- Encuentra la media y la desviación estándar para los tiempos de ciclo.
- Ha habido 46 veces que el concreto ha sido llevado al sitio de construcción. Encuentra la probabilidad de que el tiempo medio de ciclo para estas 46 muestras supere los 58 minutos.
- Las centrales nucleares experimentan accidentes graves una vez cada 8 años. Let\(X\) = el tiempo de espera hasta el siguiente accidente grave. X sigue una Distribución Exponencial en la que\(\mu\) = el tiempo de espera esperado y\(\sigma=\mu\).
- ¿Cuál es la media y la desviación estándar de la variable aleatoria X?
- Para 35 accidentes en centrales nucleares, el tiempo medio de espera fue de 6.1 años. ¿Este valor es inusualmente bajo? Para responder, encuentra la probabilidad de que el tiempo medio de espera sea de 6.1 años o menos.


