15.2.13: Capítulo 14 Tarea
- Page ID
- 151394
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)
- Un agente inmobiliario utiliza un modelo de regresión simple para estimar el valor de una vivienda en función del tamaño cuadrado en el que\(Y\) se encuentra el valor de la casa en dólares y\(X\) es el tamaño en pies cuadrados totales. La ecuación de regresión es\(\hat{Y}=253000+438 X\).
- Interpretar la pendiente usando las unidades del problema.
- Estimar el valor de una vivienda con 1347 pies cuadrados.
- ¿El coeficiente de correlación será positivo o negativo en este problema? Explique.
- Un concesionario de autos utiliza un modelo de regresión simple para estimar el valor de un Toyota Prius 2013 usado basando el valor en el kilometraje del automóvil. \(Y\)es el valor del automóvil en dólares y\(X\) es el total de millas en el cuentakilómetros. La ecuación de regresión es\(\hat{Y}=28000-0.048 X\).
- Interpreta la pendiente usando las unidades del problema.
- Estimar el valor de un automóvil con una lectura del odómetro de 143,282 millas.
- ¿Por qué este modelo no funcionaría para un Prius que fue conducido 600,000 millas?
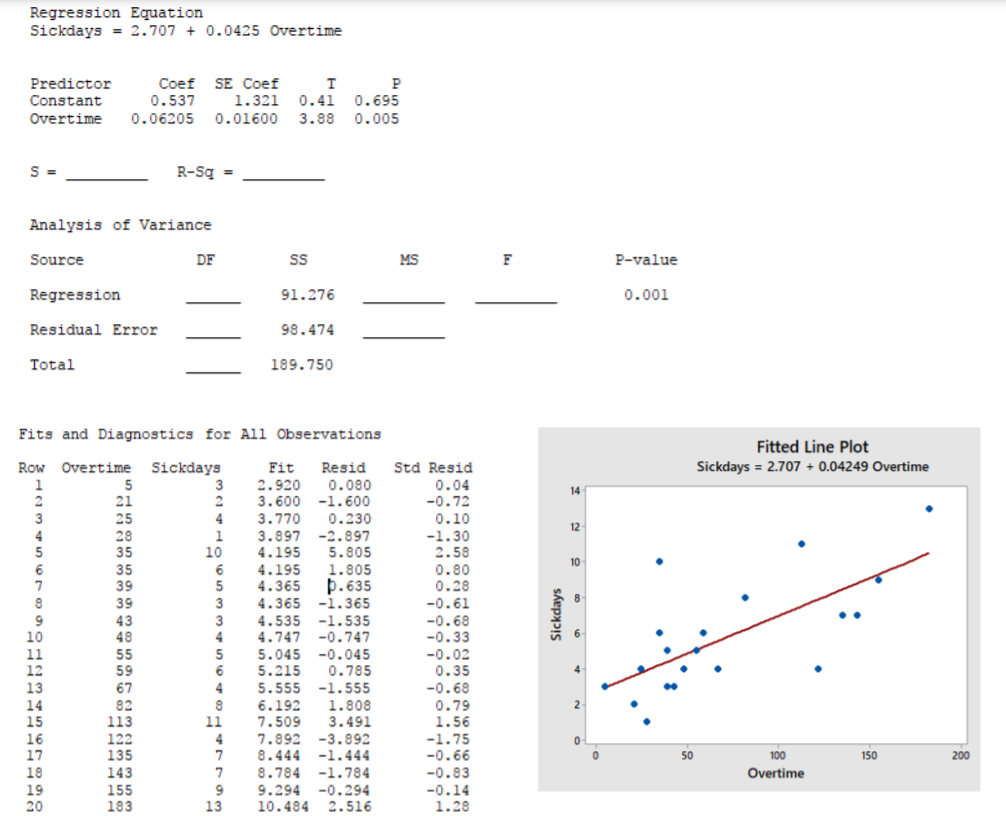
- A un directivo le preocupa que las horas extras (medidas en horas) estén contribuyendo a más enfermedades (medidas en días de enfermedad) entre los empleados. Se muestrearon los registros de datos de 20 empleados con los resultados del MINITAB mostrados al final de las preguntas.
- Identificar la Variable explicativa (Independiente) — incluir unidades.
- Identificar la variable de respuesta (dependiente) — incluir unidades.
- Encuentra la línea de menor cuadrado donde Días de Enfermedad dependa de Horas Extras. Interpreta la pendiente usando las unidades apropiadas.
- Pruebe la hipótesis de que el modelo de regresión es significativo (\(\alpha = .10\)). Mostrar todos los pasos. Rellene los valores faltantes en la tabla ANOVA.
- Encontrar e interpretar el\(r^2\) coeficiente de determinación. (Línea en blanco)
- Encuentra la estimación de la desviación estándar del error residual. (Línea en blanco)
- Identificar cualquier residuo que sea más de dos desviaciones estándar de la línea de regresión.
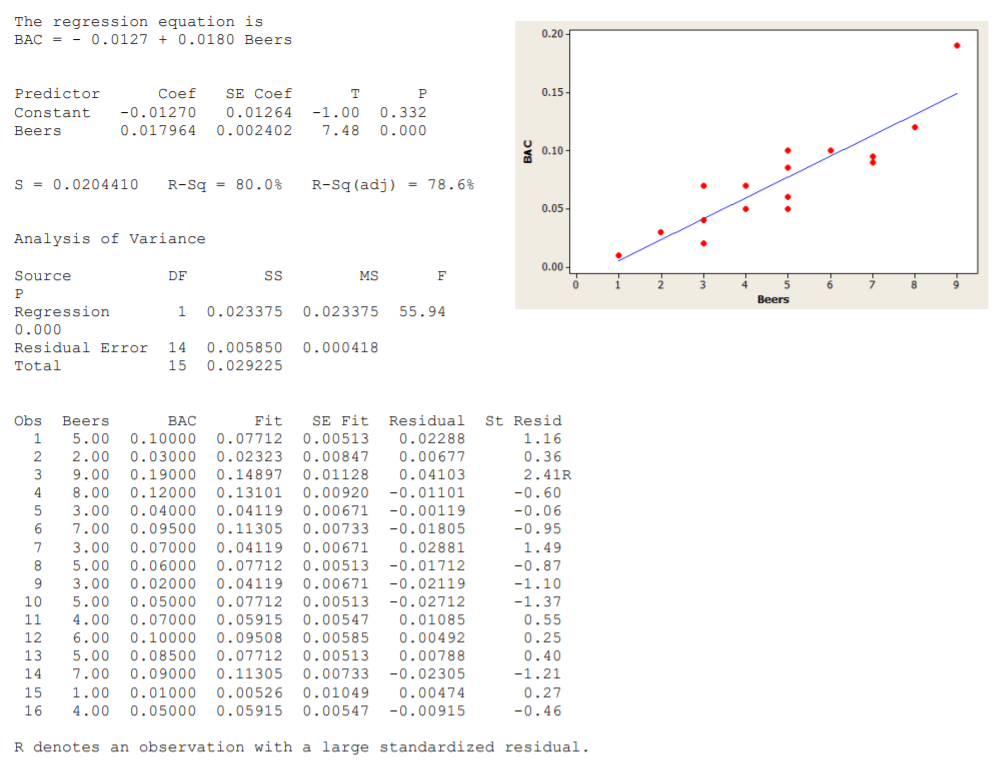
- 16 estudiantes voluntarios bebieron un número asignado al azar de latas de cerveza. Treinta minutos después un policía midió su contenido de alcohol en sangre (BAC) en gramos de alcohol por decilitro de sangre. Los datos y la salida de computadora se dan a continuación de las preguntas.
- Encuentra la línea de menor cuadrado donde el BAC es dependiente de las cervezas consumidas. Interpretar la pendiente.
- Encontrar e interpretar el estadístico r‐cuadrado.
- Probar la hipótesis de que las cervezas consumidas y BAC están correlacionadas (\(\alpha = .05\))
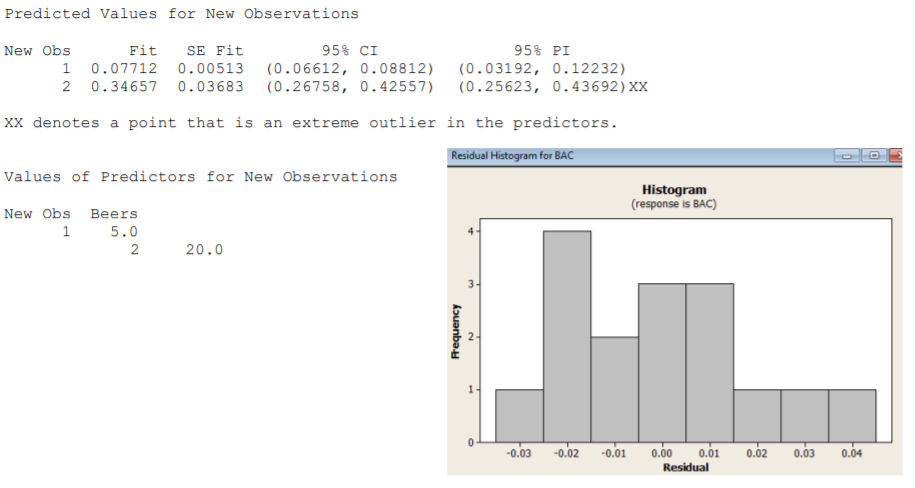
- Encuentra un Intervalo de Confianza del 95% para el BAC medio para un estudiante que consume 5 cervezas.
- ¿Este modelo sería apropiado para un estudiante que consumió 20 cervezas? Explique.
- Joe afirma que aún puede conducir legalmente después de consumir 5 cervezas: el límite legal de BAC es de 0.08. Encuentra un intervalo de predicción del 95% para Joe's BAC. ¿Crees que Joe puede conducir legalmente?
- Análisis Residual
- Esperaríamos que los residuos fueran aleatorios: cerca de la mitad serían positivos y la mitad serían negativos. Verifique los residuos reales y compare los porcentajes reales con los porcentajes esperados.
- El supuesto para la regresión es que los residuales tienen una Distribución Normal. Esto significa que aproximadamente 68% de los residuos tendrían una\(Z\) puntuación ‐entre ‐1 y 1, 95% de los residuos tendrían una\(Z\) puntuación ‐entre ‐2 y 2 y todos los residuales tendrían una puntuación Z‐score entre ‐3 y 3. La Columna etiquetada como “Residual Estandarizado” es la\(Z\) puntuación de cada residuo. Verifique qué porcentaje de los datos tiene\(Z\) ‐puntuaciones en cada uno de estos tres intervalos, y compare los porcentajes reales con los porcentajes esperados (68%, 95%, 100%).
Datos para Análisis de Regresión Ejercicio 4: BAC versus Beers
- Se utilizó el siguiente análisis de regresión para probar la Pobreza (porcentaje de población que vive por debajo del umbral de pobreza) como predictor de Abandono (Porcentaje de Deserción Escolar Secundaria).
- Cinco ítems han sido borrados; encuentra estos faltantes los cuales pueden ser calculados en base a otra información en la salida.
- \(r^2\)
- \(r\)
- Error estándar de los residuos
- \(F\)Estadística de prueba
- Valor Predicho para Pobreza = 15
- Cinco ítems han sido borrados; encuentra estos faltantes los cuales pueden ser calculados en base a otra información en la salida.

- Escribe la ecuación de regresión.
- Realizar la Prueba de Hipótesis con la que se correlacionan la Pobreza y el HSSDropout\(\alpha =.01\) (Valor Crítico para\(F\) es 7.19 (\(\alpha =.01\), Df‐num=1, Df‐den=48)).
- ¿Qué porcentaje de la variabilidad de las tasas de deserción escolar secundaria puede explicarse por la Pobreza?
- Dakota del Norte tiene una Tasa de Pobreza de 11.9 por ciento y una Tasa de Abandono de HS de 4.6 por ciento.
- Calcular la tasa de abandono del SA prevista para Dakota del Norte a partir de la ecuación de regresión.
- El Error Estándar (de la parte a‐iii) es la desviación estándar con respecto a la línea de regresión. Calcular la\(Z\) puntuación ‐para la Tasa de Abandono de HS de Dakota del Norte real de 4.6 (Restar el valor predicho y dividir por el Error Estándar). ¿Crees que la Tasa de Abandono HS de Dakota del Norte es inusual? Explique.
Para los estudios en las preguntas 6 a 8:
- Identificar la variable explicativa.
- Identificar la variable de respuesta
- Elija el modelo apropiado de entre estos tres:
- Prueba de independencia de Chi‐cuadrado
- ANOVA de un factor
- Regresión lineal simple
- Un diseñador de campos de golf estaba estudiando tipos de pasto para ser utilizado en una región que era susceptible a sequías. El diseñador estudió 5 tipos de pasto: Bent Grass, Festuca, Centeno Grass, Bermuda Grass y Paspalum. Se tomaron diez muestras de cada pasto y se regaron para mantener el pasto en condiciones óptimas durante un mes. Para cada muestra, el uso diario de agua se calculó en litros por metro cuadrado. El diseñador quería saber si había una diferencia significativa en el uso medio de agua debido al tipo de césped.
- Un psicólogo escolar cree que los alumnos que tienen más tarea van a dormir menos. 200 alumnos participaron en un estudio. Por cada uno de los 14 días consecutivos, se les pidió a los alumnos que contaran cuántos minutos pasaron haciendo sus tareas y cuántos minutos durmieron esa noche.
- ¿Fumar cambia la forma en que alguien sabe la sal? Un investigador tomó muestras de 200 fumadores y 200 no fumadores. Luego se les dio un tazón de sopa y piden clasificar el nivel de sal en una de 3 categorías: baja en sal, sal promedio y sal alta. El investigador quiso saber si había una diferencia significativa en la clasificación de salinidad debido a si el participante era fumador.


