2.1: Graficar variables cualitativas
- Page ID
- 152231
Objetivos de aprendizaje
- Crear una tabla de frecuencias
- Determinar cuándo los gráficos circulares son valiosos y cuándo no
- Crear e interpretar gráficos de barras
- Identificar errores gráficos comunes
Cuando Apple Computer presentó la computadora iMac en agosto\(1998\), la compañía quiso saber si el iMac estaba expandiendo la participación de mercado de Apple. ¿El iMac acaba de atraer a los propietarios anteriores de Macintosh? ¿O fue comprada por recién llegados al mercado de computadoras y por usuarios anteriores de Windows que estaban cambiando? Para\(500\) averiguarlo, se entrevistó a clientes del iMac. Cada cliente fue categorizado como un propietario anterior de Macintosh, un propietario anterior de Windows o un nuevo comprador de computadora.
En esta sección se examinan los métodos gráficos para mostrar los resultados de las entrevistas. Aprenderemos algunas lecciones generales sobre cómo graficar datos que caen en un pequeño número de categorías. En una sección posterior se considerará cómo graficar los datos numéricos en los que cada observación está representada por un número en algún rango. El punto clave sobre los datos cualitativos que nos ocupan en la presente sección es que no vienen con un ordenamiento preestablecido (la forma en que se ordenan los números). Por ejemplo, no existe un sentido natural en el que la categoría de usuarios anteriores de Windows venga antes o después de la categoría de usuarios anteriores de Macintosh. Esta situación puede contrastarse con datos cuantitativos, como el peso de una persona. Las personas de un peso son ordenadas naturalmente con respecto a las personas de un peso diferente.
Tablas de Frecuencia
Todos los métodos gráficos mostrados en esta sección se derivan de tablas de frecuencias. En el cuadro se\(\PageIndex{1}\) muestra una tabla de frecuencias para los resultados del estudio iMac; se muestran las frecuencias de las distintas categorías de respuesta. También se muestran las frecuencias relativas, que son la proporción de respuestas en cada categoría. Por ejemplo, la frecuencia relativa para “ninguno” es\(85/500 = 0.17\).
| Propiedad previa | Frecuencia | Frecuencia relativa |
|---|---|---|
| Ninguno | 85 | 0.17 |
| Windows | 60 | 0.12 |
| Macintosh | 355 | 0.71 |
| Total | 500 | 1.00 |
Gráficos circulares
El gráfico circular de la Figura\(\PageIndex{1}\) muestra los resultados del estudio iMac. En un gráfico circular, cada categoría está representada por una porción del pastel. El área de la porción es proporcional al porcentaje de respuestas en la categoría. Esta es simplemente la frecuencia relativa multiplicada por\(100\). Si bien la mayoría de los compradores de iMac eran propietarios de Macintosh, Apple se vio alentado por el\(12\%\) de los compradores que eran antiguos usuarios\(17\%\) de Windows, y por el de los compradores que compraban una computadora por primera vez.
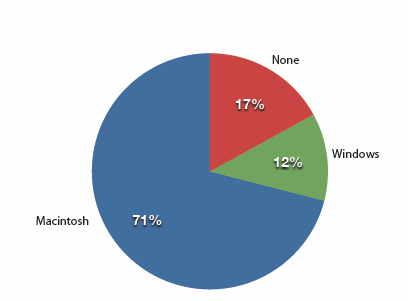
Los gráficos circulares son efectivos para mostrar las frecuencias relativas de un pequeño número de categorías. No se recomiendan, sin embargo, cuando se tiene un gran número de categorías. Los gráficos circulares también pueden ser confusos cuando se utilizan para comparar los resultados de dos encuestas o experimentos diferentes. En un influyente libro sobre el uso de gráficas, Edward Tufte afirmó: “El único diseño peor que un gráfico circular son varios de ellos”.
Aquí hay otro punto importante sobre los gráficos circulares. Si se basan en un pequeño número de observaciones, puede ser engañoso etiquetar las rebanadas de pastel con porcentajes. Por ejemplo, si solo\(5\) las personas hubieran sido entrevistadas por Apple Computers, y\(3\) fueran ex usuarios de Windows, sería engañoso mostrar un gráfico circular con el sector de Windows mostrando\(60\%\). Con tan pocas personas entrevistadas, un porcentaje tan grande de usuarios de Windows podría haber ocurrido fácilmente ya que el azar puede causar grandes errores con muestras pequeñas. En este caso, es mejor alertar al usuario del gráfico circular sobre los números reales involucrados. Por lo tanto, los cortes deben etiquetarse con las frecuencias reales observadas (e.g.,\(3\)) en lugar de con porcentajes.
Gráficos de barras
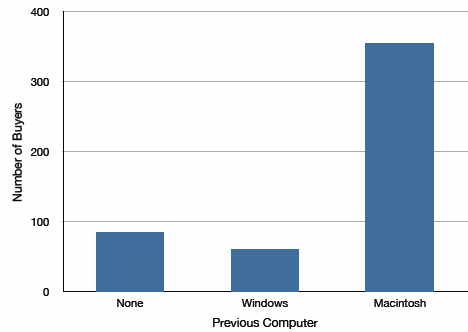
Los gráficos de barras también se pueden usar para representar frecuencias de diferentes categorías. En la Figura se muestra un gráfico de barras de las compras del iMac\(\PageIndex{2}\). Las frecuencias se muestran en el\(Y\) eje y el tipo de computadora que anteriormente poseía se muestra en el\(X\) eje. Por lo general, el\(Y\) eje -muestra el número de observaciones en cada categoría en lugar del porcentaje de observaciones como es típico en los gráficos circulares.
Comparando Distribuciones
A menudo necesitamos comparar los resultados de diferentes encuestas, o de diferentes condiciones dentro de una misma encuesta general. En este caso, estamos comparando las “distribuciones” de respuestas entre las encuestas o condiciones. Los gráficos de barras suelen ser excelentes para ilustrar las diferencias entre dos distribuciones. La figura\(\PageIndex{3}\) muestra el número de personas que juegan juegos de cartas en el sitio web de Yahoo un domingo y un miércoles en la primavera de\(2001\). Vemos que hubo más jugadores en general el miércoles en comparación con el domingo. El número de personas que interpretaron a Pinochle fue, sin embargo, el mismo en estos dos días. En contraste, había aproximadamente el doble de personas jugando corazones el miércoles que el domingo. Hechos como estos surgen claramente de un gráfico de barras bien diseñado.
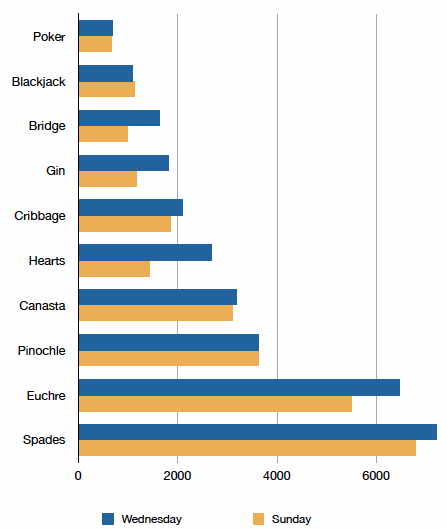
Las barras de la Figura\(\PageIndex{3}\) están orientadas horizontalmente en lugar de verticalmente. El formato horizontal es útil cuando se tienen muchas categorías porque hay más espacio para las etiquetas de categoría. Tendremos más que decir sobre los gráficos de barras cuando consideremos cantidades numéricas más adelante en la sección Gráficos de barras.
Algunos errores gráficos a evitar
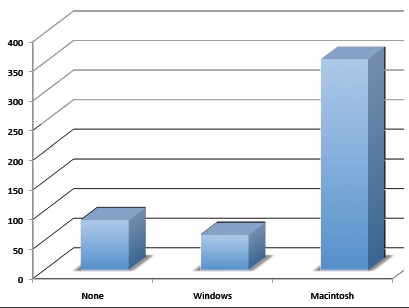
¡No te pongas elegante! La gente a veces agrega características a los gráficos que no ayudan a transmitir su información. Por ejemplo, los gráficos de barras\(3\) -dimensionales como el que se muestra en la Figura no\(\PageIndex{4}\) suelen ser tan efectivos como sus contrapartes bidimensionales.
Aquí hay otra forma en que la fantasía puede llevar a problemas. En lugar de barras lisas, es tentador sustituir imágenes significativas. Por ejemplo, Figura\(\PageIndex{5}\) presenta los datos del iMac utilizando imágenes de computadoras. Las alturas de las imágenes representan con precisión el número de compradores, sin embargo, la figura\(\PageIndex{5}\) es engañosa porque la atención del espectador será captada por las áreas. Las áreas pueden exagerar las diferencias de tamaño entre los grupos. En términos de porcentajes, la proporción de propietarios anteriores de Macintosh con respecto a propietarios anteriores de Windows está\(6\) a punto de\(1\). Pero la proporción de las dos áreas en la Figura\(\PageIndex{5}\) está\(35\) a punto de\(1\). Una persona sesgada que desee ocultar el hecho de que muchos propietarios de Windows compraron iMacs estaría tentado a usar Figura\(\PageIndex{5}\) en lugar de Figura\(\PageIndex{2}\)! Edward Tufte acuñó el término “factor mentira” para referirse a la relación entre el tamaño del efecto mostrado en una gráfica y el tamaño del efecto mostrado en los datos. Sugiere que los factores mentirosos mayores\(1.05\) o menores que\(0.95\) producen distorsiones inaceptables.

Otra distorsión en los gráficos de barras resulta de establecer la línea base en un valor distinto de cero. La línea base es la parte inferior del\(Y\) eje, representando el menor número de casos que podrían haber ocurrido en una categoría. Normalmente, pero no siempre, este número debería ser cero. La figura\(\PageIndex{6}\) muestra los datos de iMac con una línea base de\(50\). Una vez más, las diferencias en áreas sugieren una historia diferente a las verdaderas diferencias en porcentajes. El porcentaje de Windows-switchers parece minúsculo en comparación con su verdadero valor de\(12\%\).
Por último, observamos que es un grave error usar una gráfica de líneas cuando el\(X\) eje -contiene meramente variables cualitativas. Un gráfico de líneas es esencialmente un gráfico de barras con las partes superiores de las barras representadas por puntos unidos por líneas (el resto de la barra se suprime). La figura muestra de\(\PageIndex{7}\) manera inapropiada un gráfico de líneas de los datos del juego de cartas de Yahoo. El inconveniente de Figure\(\PageIndex{7}\) es que da la falsa impresión de que los juegos se ordenan naturalmente de manera numérica cuando, de hecho, están ordenados alfabéticamente.
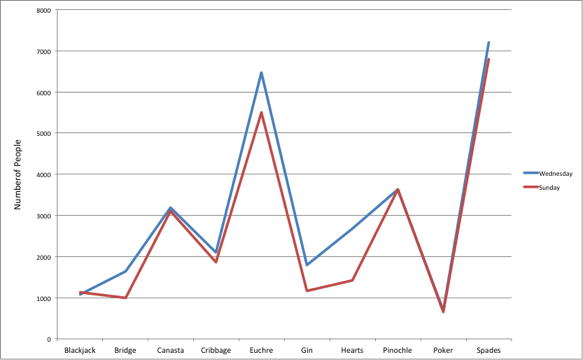
Figura\(\PageIndex{7}\): Un gráfico de líneas utilizado de manera inapropiada para representar el número de personas que juegan diferentes juegos de cartas los domingos y miércoles.
Resumen
Los gráficos circulares y los gráficos de barras pueden ser métodos efectivos para retratar datos cualitativos. Los gráficos de barras son mejores cuando hay más que unas pocas categorías y para comparar dos o más distribuciones. Tenga cuidado de evitar crear gráficas engañosas.


