2.4: Histogramas
- Page ID
- 152202
Objetivos de aprendizaje
- Crear una distribución de frecuencia agrupada
- Crear un histograma basado en una distribución de frecuencia agrupada
- Determinar un ancho de contenedor apropiado
Un histograma es un método gráfico para mostrar la forma de una distribución. Es particularmente útil cuando hay un gran número de observaciones. Comenzamos con un ejemplo consistente en las puntuaciones de\(642\) los estudiantes en una prueba de psicología. La prueba consiste en\(197\) ítems, cada uno calificado como “correcto” o “incorrecto”. Los puntajes de los estudiantes variaron de\(46\) a\(167\).
El primer paso es crear una tabla de frecuencias. Desafortunadamente, una tabla de frecuencias simple sería demasiado grande, conteniendo sobre\(100\) filas. Para simplificar la tabla, agrupamos las puntuaciones como se muestra en la Tabla\(\PageIndex{1}\).
| Límite inferior del intervalo | Límite superior del intervalo | Frecuencia de clase |
|---|---|---|
| 39.5 | 49.5 | 3 |
| 49.5 | 59.5 | 10 |
| 59.5 | 69.5 | 53 |
| 69.5 | 79.5 | 107 |
| 79.5 | 89.5 | 147 |
| 89.5 | 99.5 | 130 |
| 99.5 | 109.5 | 78 |
| 109.5 | 119.5 | 59 |
| 119.5 | 129.5 | 36 |
| 129.5 | 139.5 | 11 |
| 139.5 | 149.5 | 6 |
| 149.5 | 159.5 | 1 |
| 159.5 | 169.5 | 1 |
Para crear esta tabla, el rango de puntuaciones se dividió en intervalos, llamados intervalos de clase. El primer intervalo es de\(39.5\) a\(49.5\), el segundo de\(49.5\) a\(59.5\), etc. A continuación, se contó el número de puntuaciones que caen en cada intervalo para obtener las frecuencias de clase. Hay tres puntuaciones en el primer intervalo,\(10\) en el segundo, etc.
Los intervalos de clase de ancho\(10\) proporcionan suficientes detalles sobre la distribución para ser reveladores sin hacer que la gráfica sea demasiado “entrecortada”. Más información sobre cómo elegir los anchos de los intervalos de clase se presenta más adelante en esta sección. Colocar los límites de los intervalos de clase a medio camino entre dos números (por ejemplo,\(49.5\)) asegura que cada puntaje caerá en un intervalo en lugar de en el límite entre intervalos.
En un histograma, las frecuencias de clase están representadas por barras. La altura de cada barra corresponde a su frecuencia de clase. Un histograma de estos datos se muestra en la Figura\(\PageIndex{1}\).
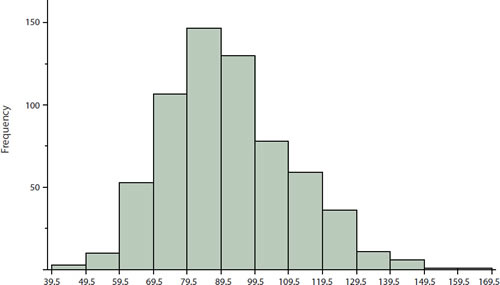
El histograma deja claro que la mayoría de las puntuaciones están en el medio de la distribución, con menos puntuaciones en los extremos. También se puede ver que la distribución no es simétrica: las puntuaciones se extienden hacia la derecha más lejos que a la izquierda. Por lo tanto, se dice que la distribución está sesgada. (Tendremos más que decir sobre las formas de las distribuciones en el capítulo "Resumiendo distribuciones”.)
En nuestro ejemplo, las observaciones son números enteros. Los histogramas también se pueden usar cuando las puntuaciones se miden en una escala más continua, como el tiempo (en milisegundos) requerido para realizar una tarea. En este caso, no hay necesidad de preocuparse por los cercas ya que son improbables. (Sería toda una coincidencia que una tarea requiriera exactamente\(7\) segundos, medidos a la milésima de segundo más cercana). Por lo tanto, somos libres de elegir números enteros como límites para nuestros intervalos de clase\(4000,\; 5000\), por ejemplo, etc. La frecuencia de clase es entonces el número de observaciones que son mayores o iguales al límite inferior, y estrictamente menores que el límite superior. Por ejemplo, un intervalo podría contener tiempos de\(4000\) a\(4999\) milisegundos. Usar números enteros como límites evita una apariencia desordenada, y es la práctica de muchos programas de computadora que crean histogramas. Tenga en cuenta también que algunos programas de computadora etiquetan la mitad de cada intervalo en lugar de los puntos finales.
Los histogramas pueden basarse en frecuencias relativas en lugar de frecuencias reales. Los histogramas basados en frecuencias relativas muestran la proporción de puntuaciones en cada intervalo en lugar del número de puntuaciones. En este caso, el\(Y\) eje -va de\(0\) a\(1\) (o algún punto intermedio si no hay proporciones extremas). Puede cambiar un histograma basado en frecuencias a uno basado en frecuencias relativas (a) dividiendo cada frecuencia de clase por el número total de observaciones, y luego (b) trazando los cocientes en el\(Y\) eje -eje (etiquetado como proporción).
Regla de Sturgos
Hay más que decir sobre los anchos de los intervalos de clase, a veces llamados anchos de bin. Su elección de ancho de contenedor determina el número de intervalos de clase. Esta decisión, junto con la elección del punto de partida para el primer intervalo, afecta la forma del histograma. Hay algunas “reglas generales” que pueden ayudarte a elegir un ancho apropiado. (Pero ten en cuenta que ninguna de las reglas es perfecta.) La regla de Sturges es establecer el número de intervalos lo más cerca posible a\(1 + \log_2(N)\), donde\(\log_2(N)\) está el\(2\) logaritmo base del número de observaciones. La fórmula también se puede escribir como\(1 + 3.3\log_2(N)\), donde\(\log_{10}(N)\) está la base logarítmica\(10\) del número de observaciones. Según la regla de Sturges,\(1000\) las observaciones se graficarían con intervalos de\(11\) clase ya que\(10\) es el entero más cercano a\(\log_2(1000)\). Preferimos la regla del arroz, que es establecer el número de intervalos en el doble de la raíz cubo del número de observaciones. En el caso de\(1000\) las observaciones, la regla del arroz arroja\(20\) intervalos en lugar de los\(11\) recomendados por la regla de Sturges. Para el ejemplo de prueba de psicología usado anteriormente, la regla de Sturges recomienda\(10\) intervalos mientras que la regla Rice recomienda\(17\). Al final, nos comprometimos y elegimos\(13\) intervalos para Figura\(\PageIndex{1}\) para crear un histograma que parecía más claro. El mejor consejo es experimentar con diferentes opciones de ancho, y elegir un histograma de acuerdo a lo bien que comunique la forma de la distribución.
Para brindar experiencia en la construcción de histogramas, hemos desarrollado una demostración interactiva. La demostración revela las consecuencias de diferentes opciones de ancho de bin y de límite inferior para el primer intervalo.
| Histograma interactivo |


