2.6: Parcelas de Caja
- Page ID
- 152233
Objetivos de aprendizaje
- Definir términos básicos que incluyen bisagras, dispersión H, escalón, valor adyacente, valor exterior y valor lejano
- Crear un diagrama de caja
- Crear trazados de caja paralelos
- Determinar si una gráfica de caja es apropiada para un conjunto de datos dado
Ya hemos discutido técnicas para representar visualmente datos (ver histogramas y polígonos de frecuencia). En esta sección, presentamos otra gráfica importante llamada trama de caja. Las gráficas de caja son útiles para identificar valores atípicos y para comparar distribuciones. Explicaremos las parcelas de caja con la ayuda de datos de un experimento en clase. Como parte del “Estudio de Caso de Interferencia Stroop”, se presentó a los estudiantes de estadística introductoria una página que contenía rectángulos\(30\) coloreados. Su tarea era nombrar los colores lo más rápido posible. Se registraron sus tiempos (en segundos). Compararemos las puntuaciones de los\(16\) hombres y\(31\) mujeres que participaron en el experimento haciendo parcelas de caja separadas para cada género. Tal visualización se dice que involucra parcelas de caja paralelas.
Hay varios pasos en la construcción de una parcela de caja. El primero se basa en los\(25^{th},\; 50^{th},\; and\; 75^{th}\) percentiles en la distribución de las puntuaciones. La figura\(\PageIndex{1}\) muestra cómo se utilizan estas tres estadísticas. Para cada género, dibujamos una caja que se extiende desde el\(25^{th}\) percentil hasta el\(75^{th}\) percentil. El\(50^{th}\) percentil se dibuja dentro de la caja. Por lo tanto,
- la parte inferior de cada caja es el\(25^{th}\) percentil,
- la parte superior es el\(75^{th}\) percentil,
- y la línea en el medio es el\(50^{th}\) percentil.
Los datos para las mujeres de nuestra muestra se muestran en la Tabla\(\PageIndex{1}\).
| 14 | 17 | 18 | 19 | 20 | 21 | 29 |
| 15 | 17 | 18 | 19 | 20 | 22 | |
| 16 | 17 | 18 | 19 | 20 | 23 | |
| 16 | 17 | 18 | 20 | 20 | 24 | |
| 17 | 18 | 18 | 20 | 21 | 24 |
Para estos datos, el\(25^{th}\) percentil es\(17\), el\(50^{th}\) percentil es\(19\), y el\(75^{th}\) percentil es\(20\). Para los hombres (cuyos datos no se muestran), el\(25^{th}\) percentil es\(19\), el\(50^{th}\) percentil es\(22.5\), y el\(75^{th}\) percentil es\(25.5\).
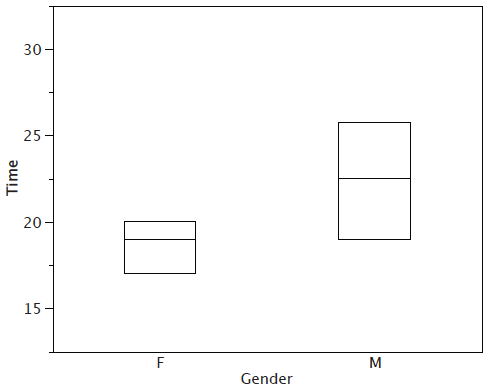
Antes de continuar, la terminología en Table\(\PageIndex{2}\) es útil.
| Nombre | Fórmula | Valor |
|---|---|---|
| Bisagra Superior | Percentil 75 | 20 |
| Bisagra Inferior | Percentil 25 | 17 |
| H-Spread | Bisagra Superior - Bisagra Inferior | 3 |
| Paso | 1.5 x Extensible en H | 4.5 |
| Cerca Interior Superior | Bisagra Superior + 1 Escalón | 24.5 |
| Cerca Interior Inferior | Bisagra Inferior - 1 Escalón | 12.5 |
| Cerca Exterior Superior | Bisagra Superior + 2 Escalones | 29 |
| Cerca Exterior Inferior | Bisagra Inferior - 2 Escalones | 8 |
| Adyacente superior | Valor más grande debajo de la cerca interior superior | 24 |
|
Inferior adyacente |
Valor más pequeño por encima de la cerca interior inferior | 14 |
| Valor Exterior | Un valor más allá de una cerca interior pero no más allá de una cerca exterior | 29 |
| Valor lejano | Un valor más allá de una cerca exterior | Ninguno |
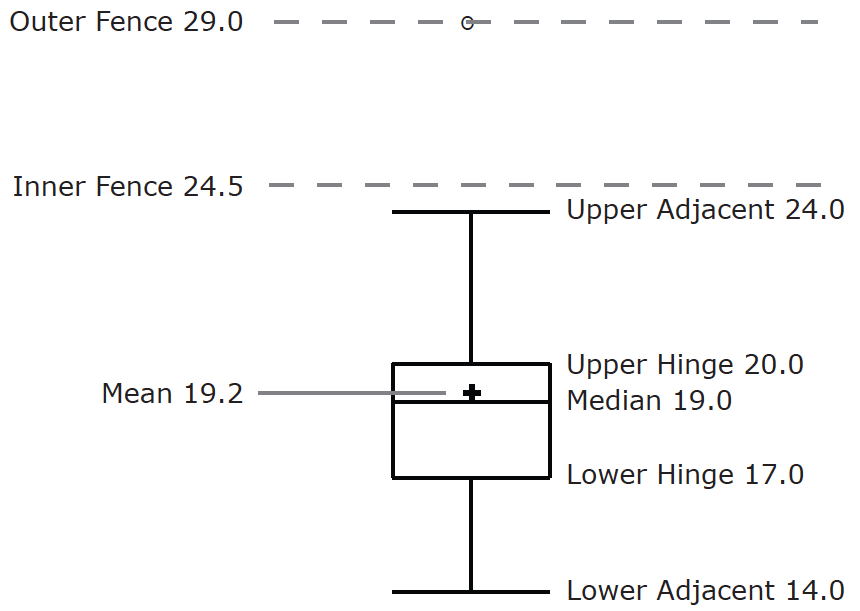
Continuando con las parcelas de caja, colocamos “bigotes” arriba y debajo de cada caja para dar información adicional sobre la propagación de los datos. Los bigotes son líneas verticales que terminan en un trazo horizontal. Los bigotes se dibujan desde las bisagras superior e inferior hasta los valores adyacentes superior e inferior (\(24\)y\(14\) para los datos de las mujeres).
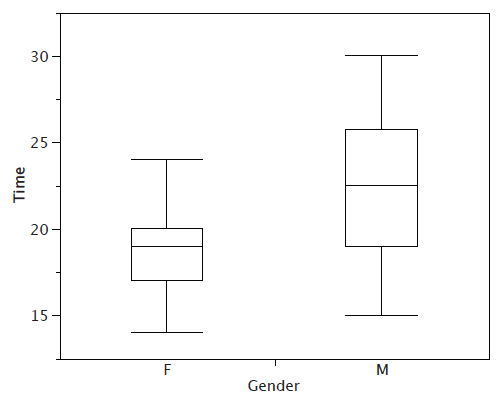
Aunque no dibujamos bigotes hasta valores externos o lejanos, todavía deseamos representarlos en nuestras parcelas de caja. Esto se logra agregando marcas adicionales más allá de los bigotes. Específicamente, los valores externos se indican con ""\(o's\) "pequeños y los valores lejanos se indican con asteriscos (\(\ast\)). En nuestros datos, no hay valores lejanos y solo un valor externo. Este valor externo de\(29\) es para las mujeres y se muestra en la Figura\(\PageIndex{3}\).
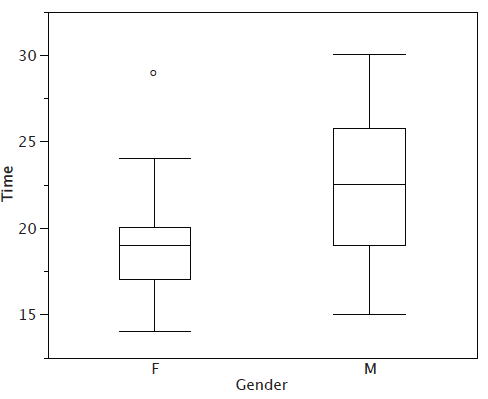
Hay una marca más para incluir en las parcelas de caja (aunque a veces se omite). Indicamos la puntuación media para un grupo insertando un signo más. La figura\(\PageIndex{4}\) muestra el resultado de sumar medias a nuestras gráficas de caja.
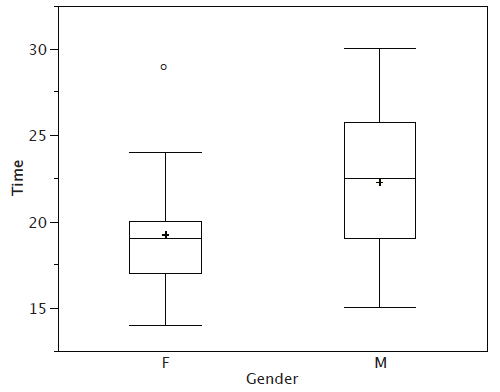
La figura\(\PageIndex{4}\) proporciona un resumen revelador de los datos. Dado que la mitad de los puntajes en una distribución están entre las bisagras (recordemos que las bisagras son los\(75^{th}\) percentiles\(25^{th}\) y), vemos que la mitad de los tiempos femeninos están entre\(17\) y\(20\) segundos, mientras que la mitad de los tiempos masculinos están entre\(19\) y\(25.5\). También vemos que las mujeres generalmente nombraban los colores más rápido que los hombres, aunque una mujer era más lenta que casi todos los hombres. En la figura se\(\PageIndex{5}\) muestra la gráfica de caja para los datos de las mujeres con etiquetas detalladas.
Las parcelas de caja proporcionan información básica sobre una distribución. Por ejemplo, una distribución con un sesgo positivo tendría un bigote más largo en la dirección positiva que en la dirección negativa. Una media mayor que la mediana también indicaría un sesgo positivo. Las parcelas de caja son buenas para retratar valores extremos y son especialmente buenas para mostrar diferencias entre distribuciones. Sin embargo, muchos de los detalles de una distribución no se revelan en una gráfica de caja, y para examinar estos detalles se debe crear un histograma y/o una visualización de tallo y hoja.
Aquí hay algunos otros ejemplos de parcelas de caja:
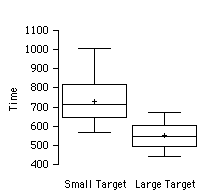
Ejemplo\(\PageIndex{1}\): Time to move the mouse over a target
Los datos provienen de una tarea en la que el objetivo es mover un mouse de computadora a un objetivo en la pantalla lo más rápido posible. En\(20\) de los ensayos, el objetivo era un rectángulo pequeño; en el otro\(20\), el objetivo era un rectángulo grande. En cada ensayo se registró el tiempo para alcanzar el objetivo. A continuación se muestran las gráficas de caja de las dos distribuciones. Se puede ver que aunque hay cierta superposición en los tiempos, generalmente tardó más tiempo en mover el mouse al objetivo pequeño que al grande.
Ejemplo\(\PageIndex{2}\): Draft lottery
En\(1969\) la guerra de Vietnam estaba en su apogeo. A una agencia llamada Servicio Selectivo se le encargó encontrar un procedimiento justo para determinar qué jóvenes serían alistados (“redactados”) en el ejército estadounidense. Se suponía que el procedimiento era justo en el sentido de no favorecer a ningún subgrupo cultural o económicamente definido de hombres estadounidenses. Se decidió que sería justo elegir a los “redactores” únicamente en función de la fecha de nacimiento de una persona. Así se ideó una lotería de cumpleaños. Trozos de papel que representan los\(366\) días del año (incluidos\(\text{February 29}\)) se colocaron en cápsulas de plástico, se vertieron en un tambor giratorio y luego se seleccionaron uno a la vez. Cuanto menor sea el número del draft, más pronto se redactaría a la persona. Los hombres con números suficientemente altos no fueron redactados en absoluto.
El primer número seleccionado fue\(258\), lo que significaba que alguien nacido el\(258^{th}\) día del año (\(\text{September 14}\)) estaría entre los primeros en ser redactados. El segundo número fue\(115\), por lo que alguien nacido el\(15^{th}\) día 1 (\(\text{April 24}\)) estuvo entre el segundo grupo en ser redactado. A todas las fechas de\(366\) nacimiento se les asignaron números de borrador de esta manera.
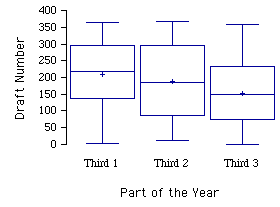
Para crear parcelas de cajas dividimos los\(366\) días del año en tercios. El primer tercio va desde\(\text{January 1 to May 1}\), el segundo desde\(\text{May 2 to August 31}\), y el último desde\(\text{September 1 to December 31}\). Los tres grupos de fechas de nacimiento arrojan tres grupos de números de borrador. El número de borrador para cada cumpleaños es el orden en que se recogió en el sorteo. La siguiente figura contiene diagramas de caja de los tres conjuntos de números de borrador. Como puede ver, las personas nacidas más adelante en el año tendían a tener números de draft más bajos.
Variaciones en parcelas de caja
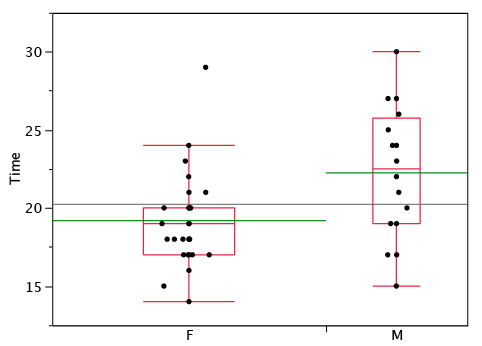
Los programas de análisis estadístico pueden ofrecer opciones sobre cómo se crean las parcelas de caja. Por ejemplo, las gráficas de caja en la Figura\(\PageIndex{8}\) se construyen a partir de nuestros datos pero difieren de las gráficas de caja anteriores de varias maneras.
- No marca valores atípicos.
- Las medias están indicadas por líneas verdes en lugar de signos más.
- La media de todas las puntuaciones se indica mediante una línea gris.
- Las puntuaciones individuales están representadas por puntos. Dado que las puntuaciones se han redondeado al segundo más cercano, cualquier punto dado podría representar más de una puntuación.
- La caja para las mujeres es más ancha que la caja para los hombres porque los anchos de las cajas son proporcionales al número de sujetos de cada género (\(31\)mujeres y\(16\) hombres).
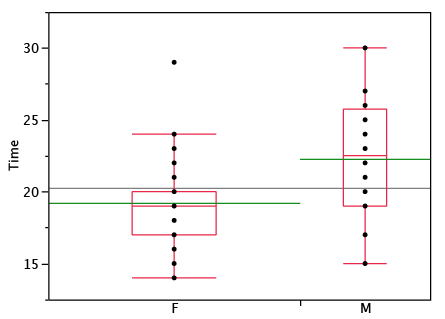
Cada punto en la Figura\(\PageIndex{8}\) representa un grupo de sujetos con la misma puntuación (redondeado al segundo más cercano). Una técnica de graficación alternativa es fluctuar los puntos. Esto significa extender diferentes puntos en la misma posición horizontal, un punto por cada sujeto. La posición horizontal exacta de un punto se determina aleatoriamente (bajo la restricción de que los diferentes puntos no se superponen exactamente). Extender los puntos te ayuda a ver múltiples ocurrencias de una puntuación determinada. Sin embargo, dependiendo del tamaño de punto y la resolución de la pantalla, algunos puntos pueden quedar oscurecidos incluso si los puntos son jittererd. La figura\(\PageIndex{9}\) muestra cómo se ve el jittering.
Los diferentes estilos de parcelas de caja son los mejores para diferentes situaciones, y no hay reglas firmes para las cuales usar. Al explorar tus datos, debes probar varias formas de visualizarlos. Las gráficas que incluyas en tu reporte deben depender de qué tan bien las diferentes gráficas revelen los aspectos de los datos que consideres más importantes.


