3.14: Estimando la simulación de varianza
- Page ID
- 152229
Objetivos de aprendizaje
- Aprender qué medida de tendencia central equilibrará una distribución
Instrucciones
Esta simulación muestra de la población de\(50\) números aquí mostrados. Se puede ver que hay\(10\) instancias de los valores\(1, 2, 3, 4\), y\(5\). Por lo tanto, la media de la población es\(3\). La varianza es la desviación cuadrada promedio de la media de\(3\). Se puede calcular que esto es exactamente\(2\).
Al hacer clic en el botón “Dibujar\(4\) números” se muestrean cuatro puntuaciones (con reemplazo) de la población. Los cuatro números se muestran en rojo, al igual que la media de los cuatro números. La varianza se calcula entonces de dos maneras. La fórmula superior calcula la varianza calculando la media de las desviaciones cuadradas o los cuatro números muestreados a partir de la media de la muestra. La fórmula inferior calcula la media de las desviaciones cuadradas o los cuatro números muestreados a partir de la media poblacional de\(3.00\) (en raras ocasiones, las medias muestrales y poblacionales serán iguales). Las varianzas calculadas se colocan en los campos a la derecha de las fórmulas. La media de los valores en un campo se muestra en la parte inferior del campo. Cuando sólo hay un valor en el campo, la media será, por supuesto, igual a ese valor.
Si vuelve a hacer clic en el botón “Dibujar\(4\) números”, se muestrearán otros cuatro números. La media y varianza también se computarán como antes. Los campos a la derecha de las fórmulas contendrán ambas varianzas y la parte inferior del campo mostrará la media de las varianzas.
La varianza poblacional es exactamente\(2\). Utilice este hecho para evaluar el valor relativo de las dos fórmulas de varianza. Ver cuál, en promedio, se acerca\(2\) y cuál da estimaciones menores. Explore si cualquiera de las fórmulas es siempre más precisa, o si a veces una es más precisa y otras, la otra fórmula lo es. Si la varianza basada en la media de la muestra se hubiera calculado dividiendo por\(N-1 = 3\) en lugar de\(4\), entonces la varianza sería\(\tfrac{4}{3}\) veces mayor. ¿Multiplicar la varianza por\(\tfrac{4}{3}\) lleva a mejores estimaciones?
Instrucciones ilustradas
Como se puede ver en la captura de pantalla a continuación, la simulación de estimación de varianza comienza mostrando una población de\(50\) números que van desde\(1 - 5\).
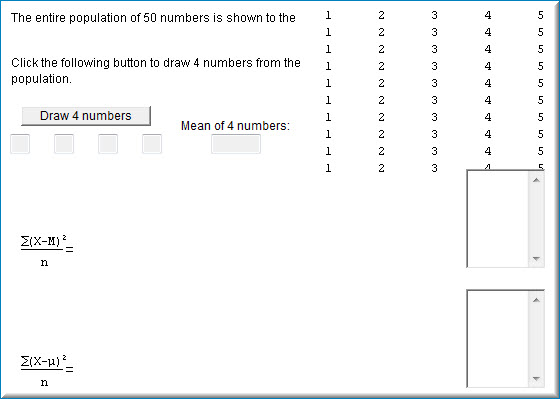
Cada vez que se hace clic en el botón “Dibujar\(4\) números” se muestrean cuatro números de la población y se calcula la media, la varianza de la muestra a partir de la media muestral así como la varianza de la muestra a partir de la media poblacional. Las varianzas se almacenan en campos próximos a su fórmula respectiva. La siguiente captura de pantalla muestra la simulación después de que se haya hecho clic cuatro veces en el botón “Dibujar\(4\) números”.
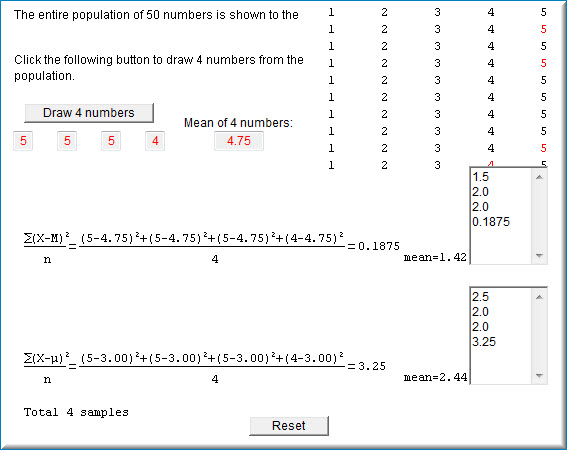
Utilice la simulación para explorar si cualquiera de las fórmulas es en promedio más precisa que la otra.


