4.E: Describiendo Datos Bivariados (Ejercicios)
- Page ID
- 152437
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Preguntas Generales
Q1
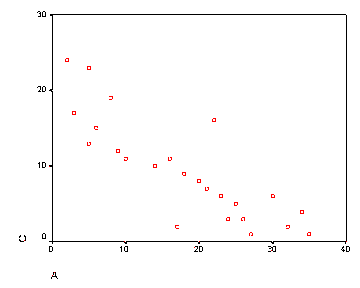
Describir la relación entre variables\(A\) y\(C\). Piensa en cosas que estas variables podrían representar en la vida real. (sección pertinente)
Q2
Conformar un conjunto de datos con\(10\) números que tenga una correlación positiva. (sección relevante y sección relevante)
Q3
Conformar un conjunto de datos con\(10\) números que tenga una correlación negativa. (sección relevante y sección relevante)
Q4
Si la correlación entre peso (en libras) y altura (en pies) es\(0.58\), encontrar: (sección relevante)
- la correlación entre peso (en libras) y altura (en yardas)
- la correlación entre peso (en kilogramos) y altura (en metros)
Q5
¿Esperarías que la correlación entre el GPA de secundaria y el GPA universitario sea mayor cuando se toma de toda tu clase de secundaria o cuando se toma solo de los mejores\(20\) estudiantes? ¿Por qué? (sección pertinente)
Q6
Para una determinada clase se examinó la relación entre la cantidad de tiempo que se dedicó a estudiar y la nota de prueba obtenida. Se determinó que a medida que aumentaba la cantidad de tiempo que estudiaban, también lo hacían sus calificaciones. ¿Es esta una asociación positiva o negativa? (sección pertinente)
Q7
Para esta misma clase, también se examinó la relación entre la cantidad de tiempo dedicado a estudiar y la cantidad de tiempo dedicado a socializar por semana. Se determinó que cuantas más horas pasaran estudiando, menos horas pasaban socializando. ¿Es esta una asociación positiva o negativa? (sección pertinente)
Q8
Para los siguientes datos: (sección pertinente)
| A | B |
| 2 | 8 |
| 5 | 5 |
| 6 | 2 |
| 8 | 4 |
| 9 | 1 |
- Encuentra los puntajes de desviación para Variable\(A\) que corresponden a los puntajes brutos de\(2\) y\(8\).
- Encuentra los puntajes de desviación para Variable\(B\) que corresponden a los puntajes brutos de\(5\) y\(4\).
- Sólo por mirar estas puntuaciones, ¿cree que estas variables\(A\) y\(B\) están correlacionadas positiva o negativamente? ¿Por qué?
- Ahora calcula la correlación. ¿Estabas en lo cierto?
Q9
Alumnos tomaron dos partes de una prueba, cada una valió\(50\) puntos. Parte\(A\) tiene una varianza de\(25\), y la Parte B tiene una varianza de\(36\). La correlación entre los puntajes de las pruebas es\(0.8\).
- Si el profesor suma las calificaciones de las dos partes juntas para formar una calificación final de prueba, ¿cuál sería la varianza de las calificaciones de las pruebas finales?
- ¿Cuál sería la varianza de Parte\(A\) - Parte\(B\)? (sección pertinente)
Q10
Verdadero/Falso: La correlación en la vida real entre la estatura y el peso es\(r=1\). (sección pertinente)
Q11
Verdadero/Falso: Es posible que las variables tengan\(r=0\) pero sigan teniendo una fuerte asociación. (sección relevante y sección relevante)
Q12
Verdadero/Falso: Dos variables con correlación de\(0.3\) tienen una relación lineal más fuerte que dos variables con una correlación de\(-0.7\). (sección pertinente)
Q13
Verdadero/Falso: Después de encuestar a cierto grupo de personas, los investigadores encontraron una\(0.5\) correlación entre el número de accidentes automovilísticos por año y la edad del conductor. Esto significa que las personas mayores se meten en más accidentes. (sección pertinente)
Q14
Verdadero/Falso: La correlación entre\(R \) y\(T\) es la misma que la correlación entre\(T\) y\(R\). (sección pertinente)
Q15
Verdadero/Falso: Para examinar gráficamente los datos bivariados, la mejor opción son dos histogramas lado a lado. (sección pertinente)
Q16
Verdadero/Falso: Una correlación de no\(r=1.2\) es posible. (sección pertinente)
Preguntas de casos prácticos
Las siguientes preguntas son del estudio de caso Angry Moods (AM).
Q17
(AM #21) ¿Cuál es la correlación entre las puntuaciones de Control-In y Control-Out? (sección pertinente)
Q18
(AM #22) ¿Esperarías que la correlación entre los puntajes de Anger-Out y Control-Out sea positiva o negativa? Calcular esta correlación. (sección relevante y sección relevante)
La siguiente pregunta es del estudio de caso Flatulencia (F).
Q19
(F #4) ¿Existe una relación entre el número de hermanos varones y la vergüenza ante intereses románticos? Crear una gráfica de dispersión y calcular r. (sección relevante y sección relevante)
Las siguientes preguntas son del estudio de caso Stroop (S).
Q20
(S #6) Crea una gráfica de dispersión que muestre “colores” en el\(Y\) eje -y “palabras” en el\(X\) eje. (sección pertinente)
Q21
(S #7) Calcular la correlación entre “colores” y “palabras”. (sección pertinente)
Q22
Ordenar los datos por tiempo de nombre de color. Elija solo los nombres de color\(20\) más rápidos y cree una gráfica de dispersión. (sección pertinente)
- ¿Cuál es la nueva correlación? (sección pertinente)
- ¿Cuál es el término técnico para el hallazgo de que esta correlación es menor que la correlación para el conjunto de datos completo? (sección pertinente)
La siguiente pregunta es del estudio de caso Animal Research (AR).
Q23
(AR #11) ¿Cuál es la correlación general entre la creencia de que la investigación animal es incorrecta y la creencia de que la investigación animal es necesaria? (sección pertinente)
La siguiente pregunta es del estudio de caso Tratamiento del TDAH (AT).
Q24
(AT #8) ¿Cuál es la correlación entre el número correcto de respuestas de los participantes después de tomar el placebo y su número correcto de respuestas después de tomar\(0.60\) mg/kg de MPH? (sección pertinente)
Seleccionar respuestas
S4
- \(0.58\)
S8
- \(-4, 2\)
S9
- \(109\)
S17
\(r = 0.72\)
S19
\(r = -0.30\)
(números más grandes para la variable “romint” significan menos vergüenza)
S 21
\(r = 0.70\)