7.2: Historia de la distribución normal
- Page ID
- 152277
Objetivos de aprendizaje
- Aprende la interesante historia de una curva normal
En el capítulo sobre probabilidad, vimos que la distribución binomial podría utilizarse para resolver problemas como “Si una moneda justa es volteada\(100\) veces, ¿cuál es la probabilidad de obtener\(60\) o más cabezas?” La probabilidad de exactamente\(x\) cabezas fuera de\(N\) volteretas se calcula usando la fórmula:
\[P(x)=\frac{N!}{x!(N-x)!}\pi ^x(1-\pi )^{N-x}\]
donde\(x\) es el número de cabezas (\(60\)),\(N\) es el número de volteretas (\(100\)), y\(\pi\) es la probabilidad de una cabeza (\(0.5\)). Por lo tanto, para resolver este problema, se calcula la probabilidad de\(60\) cabezas, luego la probabilidad de\(61\)\(62\) cabezas, cabezas, etc., y se suman todas estas probabilidades. Imagínese cuánto tiempo debió haber tardado en computar las probabilidades binomiales antes del advenimiento de las calculadoras y las computadoras.
Abraham de Moivre, estadístico\(18^{th}\) del siglo y consultor de los apostadores, a menudo fue llamado a realizar estos largos computaciones. de Moivre señaló que cuando el número de eventos (volteos de monedas) aumentaba, la forma de la distribución binomial se acercaba a una curva muy suave. Las distribuciones binomiales para\(2\)\(4\), y\(12\) volteretas se muestran en la Figura\(\PageIndex{1}\).
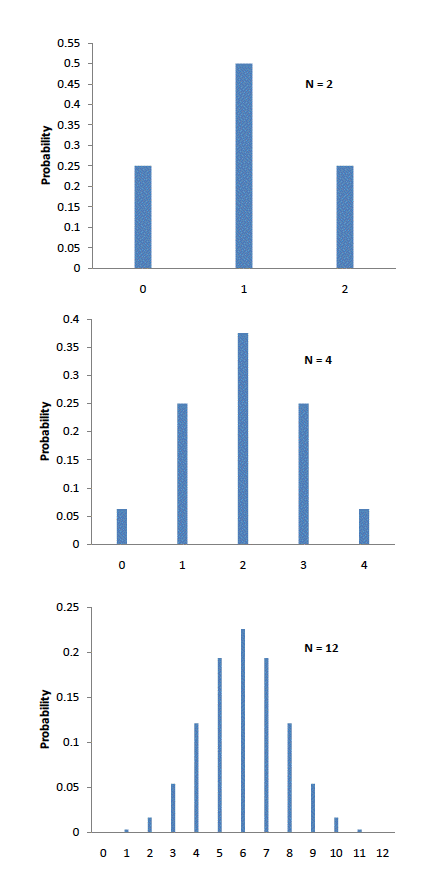
de Moivre razonó que si pudiera encontrar una expresión matemática para esta curva, sería capaz de resolver problemas como encontrar la probabilidad de\(60\) o más cabezas fuera de volteretas de\(100\) monedas mucho más fácilmente. Esto es exactamente lo que hizo, y la curva que descubrió ahora se llama la “curva normal”.
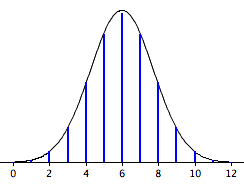
La curva suave en la Figura\(\PageIndex{2}\) es la distribución normal. Observe lo bien que se aproxima a las probabilidades binomiales representadas por las alturas de las líneas azules.
La importancia de la curva normal se deriva principalmente del hecho de que las distribuciones de muchos fenómenos naturales están al menos aproximadamente distribuidas normalmente. Una de las primeras aplicaciones de la distribución normal fue al análisis de errores de medición realizados en observaciones astronómicas, errores que ocurrieron por instrumentos imperfectos y observadores imperfectos. Galileo en el\(17^{th}\) siglo señaló que estos errores eran simétricos y que los errores pequeños ocurrieron con mayor frecuencia que los errores grandes. Esto llevó a varias distribuciones hipotéticas de errores, pero no fue hasta principios de\(19^{th}\) siglo cuando se descubrió que estos errores siguieron una distribución normal. Independientemente, los matemáticos Adrain en\(1808\) y Gauss en\(1809\) desarrollaron la fórmula para la distribución normal y mostraron que los errores se ajustaban bien a esta distribución.
Esta misma distribución había sido descubierta por Laplace en\(1778\) cuando derivó el teorema del límite central sumamente importante, el tema de una sección posterior de este capítulo. Laplace mostró que incluso si una distribución no se distribuye normalmente, las medias de muestras repetidas de la distribución estarían casi distribuidas normalmente, y que cuanto mayor sea el tamaño de la muestra, más cerca estaría la distribución de medias a una distribución normal.
La mayoría de los procedimientos estadísticos para probar diferencias entre medias asumen distribuciones normales. Debido a que la distribución de las medias es muy cercana a lo normal, estas pruebas funcionan bien aunque la distribución original sólo sea aproximadamente normal.
Quételet fue el primero en aplicar la distribución normal a las características humanas. Señaló que características como la altura, el peso y la resistencia se distribuyeron normalmente.


