9.7: Distribución de muestreo de r de Pearson
- Page ID
- 152455
Objetivos de aprendizaje
- Transformar\(r\) a\(z'\)
- Calcular la probabilidad de obtener un valor\(r\) por encima de un valor especificado
Supongamos que la correlación entre los puntajes SAT cuantitativos y verbales en una población determinada es\(0.60\). En otras palabras,\(\rho =0.60\). Si\(12\) los estudiantes fueran muestreados aleatoriamente, la correlación muestral\(r\),, no sería exactamente igual a\(0.60\). Naturalmente diferentes muestras de\(12\) estudiantes producirían diferentes valores de\(r\). La distribución de valores de\(r\) después de muestras repetidas de\(12\) estudiantes es la distribución muestral de\(r\).
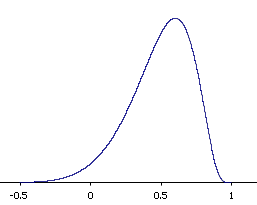
La forma de la distribución de\(r\) muestreo del ejemplo anterior se muestra en la Figura\(\PageIndex{1}\). Se puede ver que la distribución de muestreo no es simétrica: está sesgada negativamente. La razón del sesgo es que\(r\) no puede tomar valores mayores que\(1.0\) y por lo tanto la distribución no puede extenderse tan lejos en la dirección positiva como puede en la dirección negativa. Cuanto mayor sea el valor de\(\rho\), más pronunciado es el sesgo.
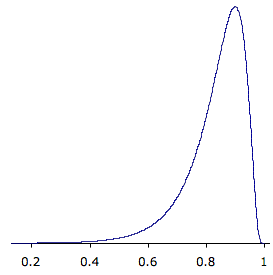
La figura\(\PageIndex{2}\) muestra la distribución de muestreo para\(\rho =0.90\). Esta distribución tiene una cola positiva muy corta y una cola larga negativa.
Refiriéndose de nuevo al ejemplo del SAT, supongamos que quería saber la probabilidad de que en una muestra de\(12\) alumnos, el valor muestral de\(r\) sea\(0.75\) o superior. Se podría pensar que todo lo que necesitaría saber para calcular esta probabilidad es la media y el error estándar de la distribución de muestreo de\(r\). No obstante, dado que la distribución del muestreo no es normal, todavía no se podría resolver el problema. Afortunadamente, el estadístico Fisher desarrolló una forma de transformarse\(r\) a una variable que normalmente se distribuye con un error estándar conocido. Se llama a la variable\(z'\) y a continuación se da la fórmula para la transformación.
\[z' = 0.5\: \ln \frac{1+r}{1-r}\]
Los detalles de la fórmula no son importantes aquí ya que normalmente usarás ya sea una tabla, Pearson r a Fisher z' o calculadora para hacer la transformación. Lo importante es que\(z'\) se distribuya normalmente y tenga un error estándar de
\[\frac{1}{\sqrt{N-3}}\]
donde\(N\) está el número de pares de puntajes.
Ejemplo\(\PageIndex{1}\)
Volvamos a la cuestión de determinar la probabilidad de obtener una correlación muestral de\(0.75\) o superior en una muestra\(12\) de una población con una correlación de\(0.60\).
Solución
El primer paso es convertir ambos\(0.60\) y\(0.75\) a sus\(z'\) valores, que son\(0.693\) y\(0.973\), respectivamente.
El error estándar de\(z'\) for\(N = 12\) es\(0.333\).
Por lo tanto, la pregunta se reduce a lo siguiente: dada una distribución normal con una media de\(0.693\) y una desviación estándar de\(0.333\), ¿cuál es la probabilidad de obtener un valor de\(0.973\) o superior?
La respuesta se puede encontrar directamente desde el applet “Calcular Área para una X dada” a ser\(0.20\).
Alternativamente, podrías usar la fórmula:
\[z = \frac{X - \mu }{\sigma } = \frac{0.973 - 0.693}{0.333} = 0.841\]
y usa una mesa para encontrar que el área de arriba\(0.841\) es\(0.20\).


