14.5: Estadística inferencial para b y r
- Page ID
- 152341
Objetivos de aprendizaje
- Indicar los supuestos en los que se basan las estadísticas inferenciales en regresión
- Identificar heterocedasticidad en un diagrama de dispersión
- Calcular el error estándar de una pendiente
- Probar la significancia de una pendiente
- Construir un intervalo de confianza en una pendiente
- Probar una correlación para determinar la significancia
En esta sección se muestra cómo realizar pruebas de significancia y calcular intervalos de confianza para la pendiente de regresión y la correlación de Pearson. Como verá, si la pendiente de regresión es significativamente diferente de cero, entonces el coeficiente de correlación también es significativamente diferente de cero.
Supuestos
Aunque no se necesitaron supuestos para determinar la línea recta que mejor se ajusta, se hacen suposiciones en el cálculo de las estadísticas inferenciales. Naturalmente, estos supuestos se refieren a la población, no a la muestra.
- Linealidad: La relación entre las dos variables es lineal.
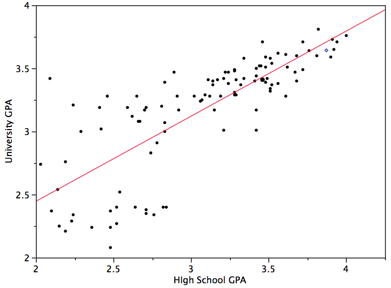
- Homocedasticidad: La varianza alrededor de la línea de regresión es la misma para todos los valores de\(X\). Una clara violación de esta suposición se muestra en la Figura\(\PageIndex{1}\). Observe que las predicciones para estudiantes con GPA de secundaria son muy buenas, mientras que las predicciones para estudiantes con GPA bajos de secundaria no son muy buenas. En otras palabras, los puntos para los estudiantes con GPA de secundaria están cerca de la línea de regresión, mientras que los puntos para los estudiantes con GPA de secundaria baja no lo están.
- Los errores de predicción se distribuyen normalmente. Esto significa que las desviaciones de la línea de regresión se distribuyen normalmente. No significa eso\(X\) o\(Y\) se distribuye normalmente.
Prueba de significancia para el talud (b)
Recordemos la fórmula general para una prueba t:
\[t=\frac{\text{statistic-hypothesized value}}{\text{estimated standard error of the statistic}}\]
Como se aplica aquí, el estadístico es el valor muestral de la pendiente (\(b\)) y el valor hipotético es\(0\). El número de grados de libertad para esta prueba es:
\[df = N-2\]
donde\(N\) está el número de pares de puntajes.
El error estándar estimado de b se calcula utilizando la siguiente fórmula:
\[s_b=\frac{s_{est}}{\sqrt{SSX}}\]
donde\(s_b\) está el error estándar estimado de\(b\),\(s_{est}\) es el error estándar de la estimación, y\(SSX\) es la suma de las desviaciones cuadradas\(X\) de la media de\(X\). \(SSX\)se calcula como
\[SSX=\sum (X-M_X)^2\]
donde\(M_x\) esta la media de\(X\). Como se mostró anteriormente, el error estándar de la estimación se puede calcular como
\[s_{est}=\sqrt{\frac{(1-r^2)SSY}{N-2}}\]
Estas fórmulas se ilustran con los datos mostrados en la Tabla\(\PageIndex{1}\). Estos datos se reproducen de la sección introductoria. La columna\(X\) tiene los valores de la variable predictora y la columna\(Y\) tiene los valores de la variable criterio. La tercera columna,\(x\), contiene las diferencias entre los valores de columna\(X\) y la media de\(X\). La cuarta columna,\(x_2\), es el cuadrado de la\(x\) columna. La quinta columna,\(y\), contiene las diferencias entre los valores de columna\(Y\) y la media de\(Y\). La última columna,\(y_2\), es simplemente cuadrada de la\(y\) columna.
| X | Y | x | x2 | y | y2 | |
|---|---|---|---|---|---|---|
| 1.00 | 1.00 | -2.00 | 4 | -1.06 | 1.1236 | |
| 2.00 | 2.00 | -1.00 | 1 | -0.06 | 0.0036 | |
| 3.00 | 1.30 | 0.00 | 0 | -0.76 | 0.5776 | |
| 4.00 | 3.75 | 1.00 | 1 | 1.69 | 2.8561 | |
| 5.00 | 2.25 | 2.00 | 4 | 0.19 | 0.0361 | |
| Suma | 15.00 | 10.30 | 0.00 | 10.00 | 0.00 | 4.5970 |
El cálculo del error estándar de la estimación (\(s_{est}\)) para estos datos se muestra en la sección sobre el error estándar de la estimación. Es igual a\(0.964\).
\[s_{est} = 0.964\]
\(SSX\)es la suma de las desviaciones cuadradas de la media de\(X\). Es, por tanto, igual a la suma de la\(x^2\) columna y es igual a\(10\).
\[SSX = 10.00\]
Ahora tenemos toda la información para calcular el error estándar de\(b\):
\[s_b=\frac{0.964}{\sqrt{10}}=0.305\]
Como se mostró anteriormente, la pendiente (\(b\)) es\(0.425\). Por lo tanto,
\[t=\frac{0.425}{0.305}=1.39\]
\[df = N-2 = 5-2 = 3\]
El\(p\) valor para una\(t\) prueba de dos colas es\(0.26\). Por lo tanto, la pendiente no es significativamente diferente de\(0\).
Intervalo de confianza para la pendiente
El método para calcular un intervalo de confianza para la pendiente poblacional es muy similar a los métodos para calcular otros intervalos de confianza. Para el intervalo de\(95\%\) confianza, la fórmula es:
\[\text{lower limit}: b - (t_{0.95})(s_b)\]
\[\text{upper limit}: b + (t_{0.95})(s_b)\]
donde\(t_{0.95}\) es el valor de\(t\) usar para el intervalo de\(95\%\) confianza.
Los valores de\(t\) a utilizar en un intervalo de confianza se pueden buscar en una tabla de la distribución t. Una versión pequeña de dicha tabla se muestra en la Tabla\(\PageIndex{2}\). La primera columna,\(df\), significa grados de libertad.
| df | 0.95 | 0.99 |
|---|---|---|
| 2 | 4.303 | 9.925 |
| 3 | 3.182 | 5.841 |
| 4 | 2.776 | 4.604 |
| 5 | 2.571 | 4.032 |
| 8 | 2.306 | 3.355 |
| 10 | 2.228 | 3.169 |
| 20 | 2.086 | 2.845 |
| 50 | 2.009 | 2.678 |
| 100 | 1.984 | 2.626 |
También puede usar la calculadora de “distribución t inversa” para encontrar los\(t\) valores a usar en un intervalo de confianza.
Aplicando estas fórmulas a los datos de ejemplo,
\[\text{lower limit}: 0.425 - (3.182)(0.305) = -0.55\]
\[\text{upper limit}: 0.425 + (3.182)(0.305) = 1.40\]
Prueba de significancia para la correlación
La fórmula para una prueba de significancia de la correlación de Pearson se muestra a continuación:
\[t=\frac{r\sqrt{N-2}}{\sqrt{1-r^2}}\]
donde\(N\) está el número de pares de puntajes. Para los datos de ejemplo,
\[t=\frac{0.627\sqrt{5-2}}{\sqrt{1-0.627^2}}=1.39\]
Observe que este es el mismo\(t\) valor obtenido en la\(t\) prueba de\(b\). Al igual que en esa prueba, los grados de libertad lo son\(N - 2 = 5 -2 = 3\).


